
Question and Answers Forum
Question Number 168744 by LEKOUMA last updated on 16/Apr/22
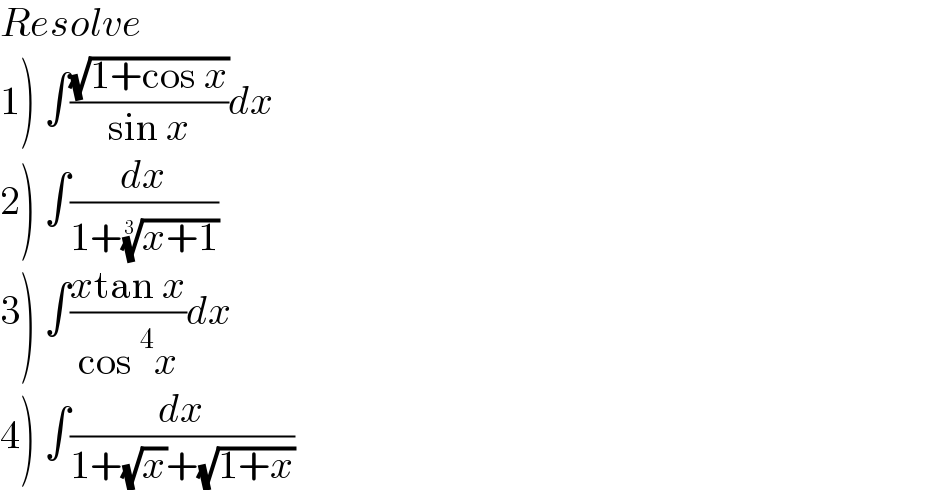
Answered by bobhans last updated on 17/Apr/22
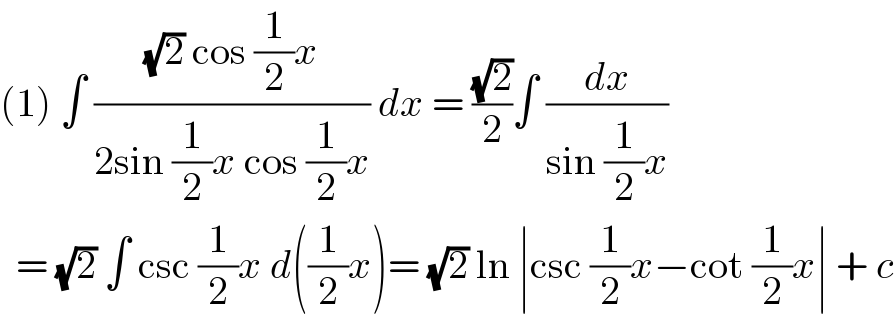
Answered by bobhans last updated on 17/Apr/22
![(2) ∫ (dx/(1+((x+1))^(1/3) )) ; [ x=t^3 −1 ] = ∫ ((3t^2 dt)/(1+t)) = 3∫ (((t+1)^2 −2t−1)/(1+t)) dt = 3[ ∫ (t+1)dt−∫ ((2(t+1)−1)/(1+t)) dt ] = 3 [(((t+1)^2 )/2)−2t+ln ∣1+t∣ ] +c = 3[ ((1+((x+1))^(1/3) )/2) −2((x+1))^(1/3) +ln ∣1+((x+1))^(1/3) ∣ ]+c](Q168770.png)
Answered by MJS_new last updated on 17/Apr/22
![∫(dx/(1+(√x)+(√(x+1))))= [t=(√x)+(√(x+1)) → dx=((2(√x)(√(x+1)))/t)dt; x=(((t^2 −1)^2 )/(4t^2 ))] =(1/2)∫(((t−1)(t^2 +1))/t^3 )dt= =(1/2)∫(1−(1/t)+(1/t^2 )−(1/t^3 ))dt= =(t/2)−(1/2)ln t −(1/(2t))+(1/(4t^2 ))= =((x+2(√x)−(√x)(√(x+1))−ln ((√x)+(√(x+1))))/2)+C](Q168802.png)
| ||
Question and Answers Forum | ||
Question Number 168744 by LEKOUMA last updated on 16/Apr/22 | ||
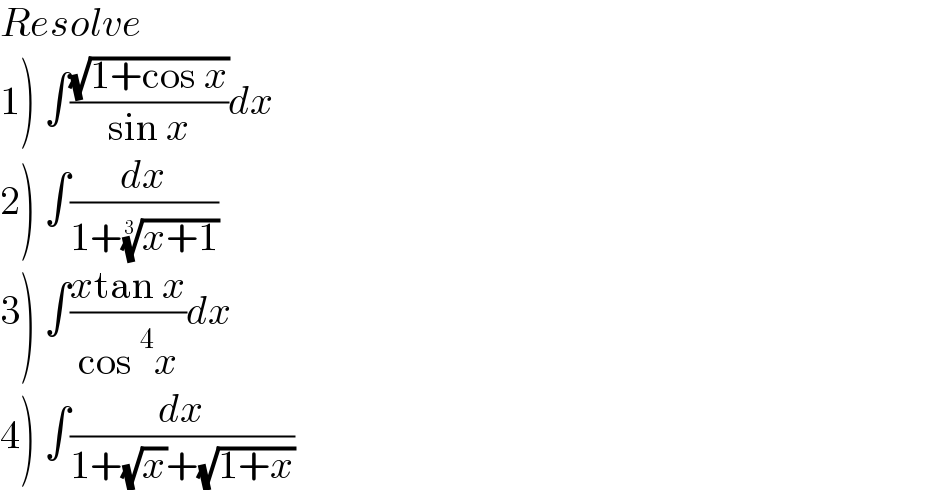 | ||
Answered by bobhans last updated on 17/Apr/22 | ||
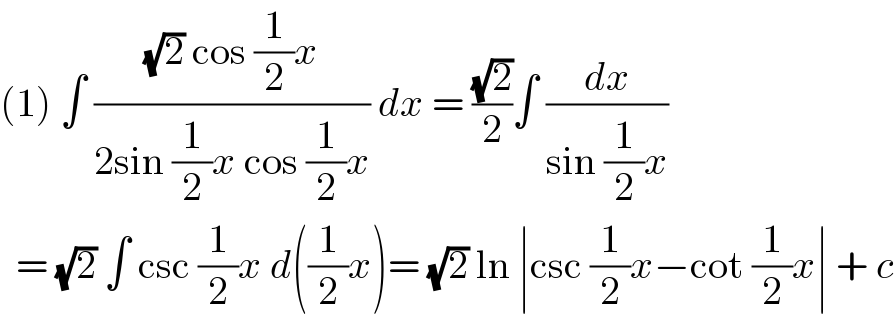 | ||
| ||
Answered by bobhans last updated on 17/Apr/22 | ||
![(2) ∫ (dx/(1+((x+1))^(1/3) )) ; [ x=t^3 −1 ] = ∫ ((3t^2 dt)/(1+t)) = 3∫ (((t+1)^2 −2t−1)/(1+t)) dt = 3[ ∫ (t+1)dt−∫ ((2(t+1)−1)/(1+t)) dt ] = 3 [(((t+1)^2 )/2)−2t+ln ∣1+t∣ ] +c = 3[ ((1+((x+1))^(1/3) )/2) −2((x+1))^(1/3) +ln ∣1+((x+1))^(1/3) ∣ ]+c](Q168770.png) | ||
| ||
Answered by MJS_new last updated on 17/Apr/22 | ||
![∫(dx/(1+(√x)+(√(x+1))))= [t=(√x)+(√(x+1)) → dx=((2(√x)(√(x+1)))/t)dt; x=(((t^2 −1)^2 )/(4t^2 ))] =(1/2)∫(((t−1)(t^2 +1))/t^3 )dt= =(1/2)∫(1−(1/t)+(1/t^2 )−(1/t^3 ))dt= =(t/2)−(1/2)ln t −(1/(2t))+(1/(4t^2 ))= =((x+2(√x)−(√x)(√(x+1))−ln ((√x)+(√(x+1))))/2)+C](Q168802.png) | ||
| ||