
Question and Answers Forum
Question Number 168966 by cortano1 last updated on 22/Apr/22
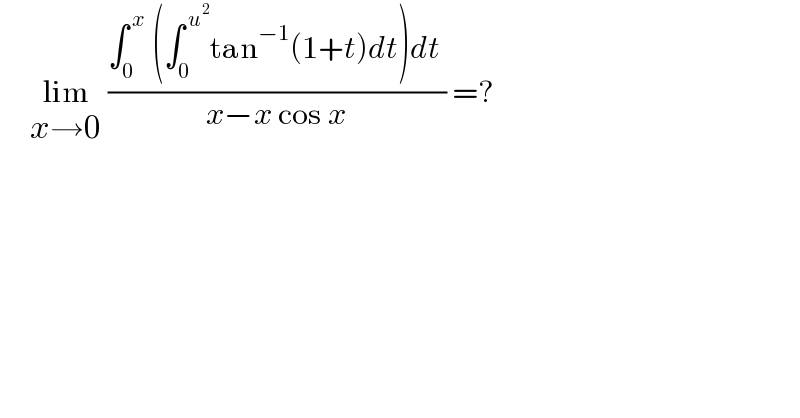
Answered by bobhans last updated on 22/Apr/22
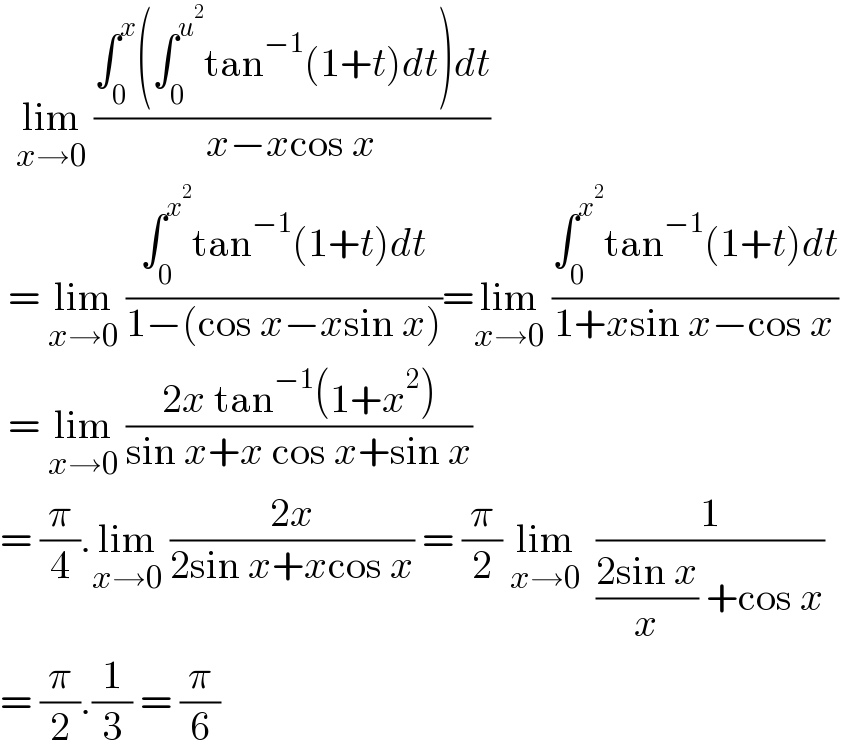
Answered by qaz last updated on 22/Apr/22
![arctan (1+t)=arctan 1+arctan (t/(2+t))=(π/4)+arctan (1−(1/(1+(t/2)))) =(π/4)+arctan[1−(1−(t/2)+...)]=(π/4)+o(1)........(t→0) ⇒ lim _(x→0) ((∫_0 ^( x) (∫_0 ^( u^2 ) tan^(−1) (1+t)dt)dt )/(x−x cos x)) =lim_(x→0) ((∫_0 ^x ∫_0 ^u^2 [(π/4)+o(1)]dtdu)/((1/2)x^3 +o(x^3 ))) =lim_(x→0) ((∫_0 ^x [(π/4)u^2 +o(u^2 )]du)/((1/2)x^3 +o(x^3 ))) =lim_(x→0) (((π/(12))x^3 +o(x^3 ))/((1/2)x^3 +o(x^3 ))) =(π/6)](Q168970.png)
| ||
Question and Answers Forum | ||
Question Number 168966 by cortano1 last updated on 22/Apr/22 | ||
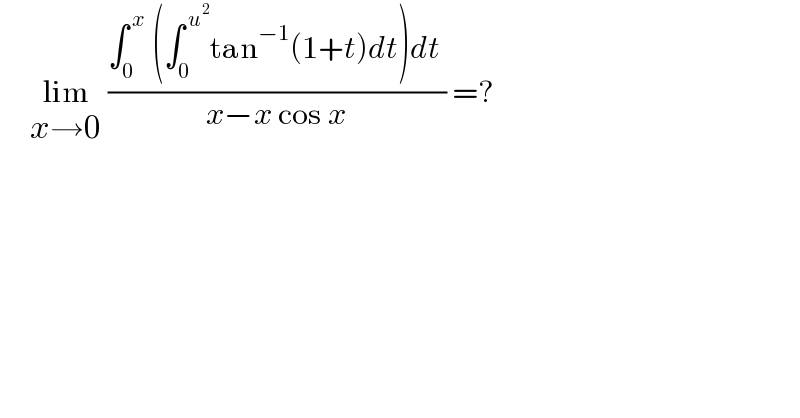 | ||
Answered by bobhans last updated on 22/Apr/22 | ||
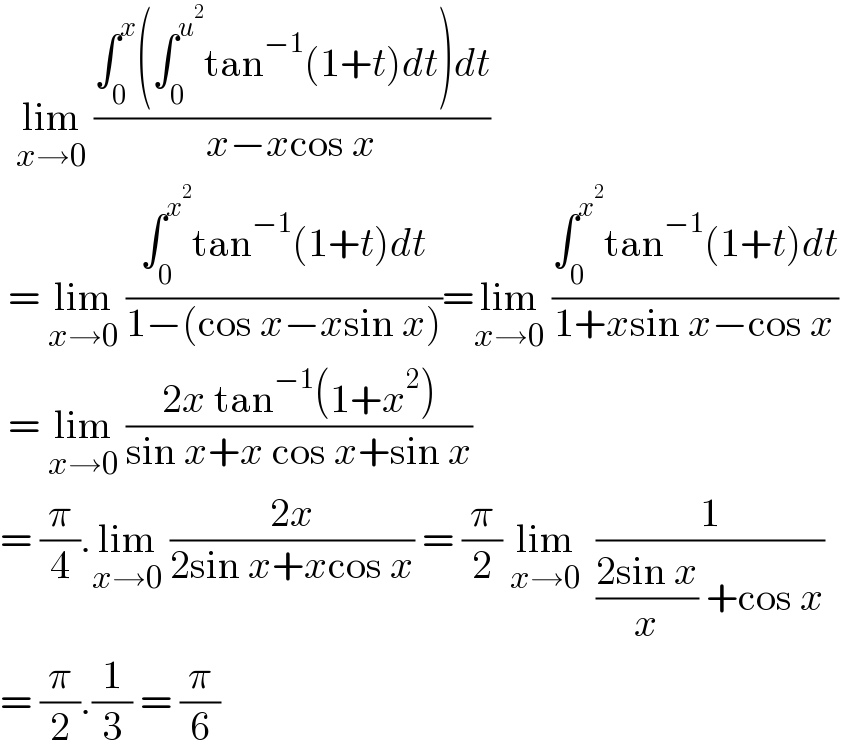 | ||
| ||
Answered by qaz last updated on 22/Apr/22 | ||
![arctan (1+t)=arctan 1+arctan (t/(2+t))=(π/4)+arctan (1−(1/(1+(t/2)))) =(π/4)+arctan[1−(1−(t/2)+...)]=(π/4)+o(1)........(t→0) ⇒ lim _(x→0) ((∫_0 ^( x) (∫_0 ^( u^2 ) tan^(−1) (1+t)dt)dt )/(x−x cos x)) =lim_(x→0) ((∫_0 ^x ∫_0 ^u^2 [(π/4)+o(1)]dtdu)/((1/2)x^3 +o(x^3 ))) =lim_(x→0) ((∫_0 ^x [(π/4)u^2 +o(u^2 )]du)/((1/2)x^3 +o(x^3 ))) =lim_(x→0) (((π/(12))x^3 +o(x^3 ))/((1/2)x^3 +o(x^3 ))) =(π/6)](Q168970.png) | ||
| ||