
Question Number 169004 by mathlove last updated on 23/Apr/22
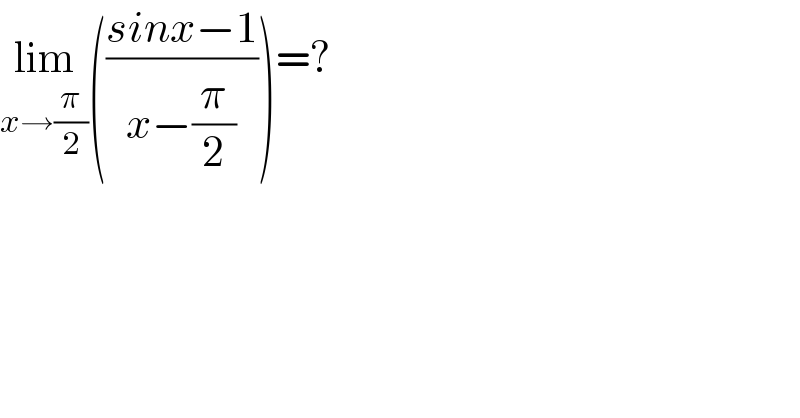
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left(\frac{{sinx}−\mathrm{1}}{{x}−\frac{\pi}{\mathrm{2}}}\right)=? \\ $$
Commented by infinityaction last updated on 23/Apr/22

$$\:\:\:\:\:\:\:\:\:\:\:\left({let}\right){p}\:\:\:\:\:\:\:\:=\:\:\:\:\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:{x}−\mathrm{sin}\:\frac{\pi}{\mathrm{2}}}{{x}−\frac{\pi}{\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{p}\:\:\:\:=\:\:\:\:\:\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\left\{\frac{\mathrm{2cos}\:\left(\frac{{x}+\pi/\mathrm{2}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{{x}−\pi/\mathrm{2}}{\mathrm{2}}\right)}{\mathrm{2}\left(\frac{{x}−\pi/\mathrm{2}}{\mathrm{2}}\right)}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:{p}\:\:\:\:=\:\:\:\:\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{p}\:\:\:\:\:\:=\:\:\:\:\mathrm{0} \\ $$$$ \\ $$
Commented by mathlove last updated on 23/Apr/22
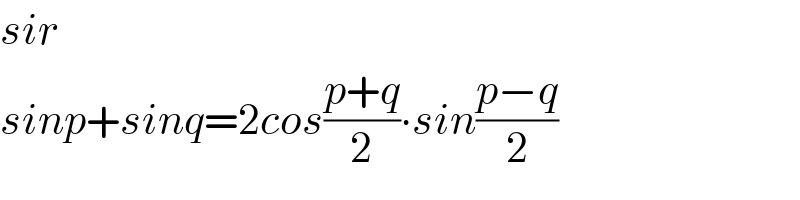
$${sir} \\ $$$${sinp}+{sinq}=\mathrm{2}{cos}\frac{{p}+{q}}{\mathrm{2}}\centerdot{sin}\frac{{p}−{q}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 23/Apr/22
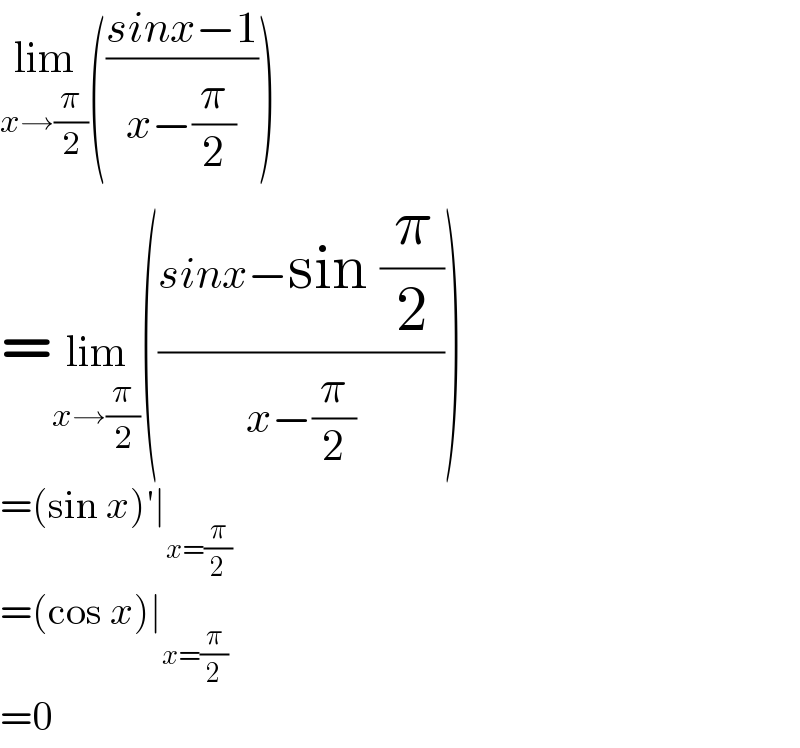
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left(\frac{{sinx}−\mathrm{1}}{{x}−\frac{\pi}{\mathrm{2}}}\right) \\ $$$$=\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left(\frac{{sinx}−\mathrm{sin}\:\frac{\pi}{\mathrm{2}}}{{x}−\frac{\pi}{\mathrm{2}}}\right) \\ $$$$=\left(\mathrm{sin}\:{x}\right)'\mid_{{x}=\frac{\pi}{\mathrm{2}}} \\ $$$$=\left(\mathrm{cos}\:{x}\right)\mid_{{x}=\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{0} \\ $$
Answered by qaz last updated on 23/Apr/22

$$\underset{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{1}}{\mathrm{x}−\frac{\pi}{\mathrm{2}}}=\underset{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\frac{\mathrm{sin}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{2}}\right)−\mathrm{1}}{\left(\mathrm{x}+\frac{\pi}{\mathrm{2}}\right)−\frac{\pi}{\mathrm{2}}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{x}−\mathrm{1}}{\mathrm{x}}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}=\mathrm{0} \\ $$
