Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 169053 by Mastermind last updated on 23/Apr/22

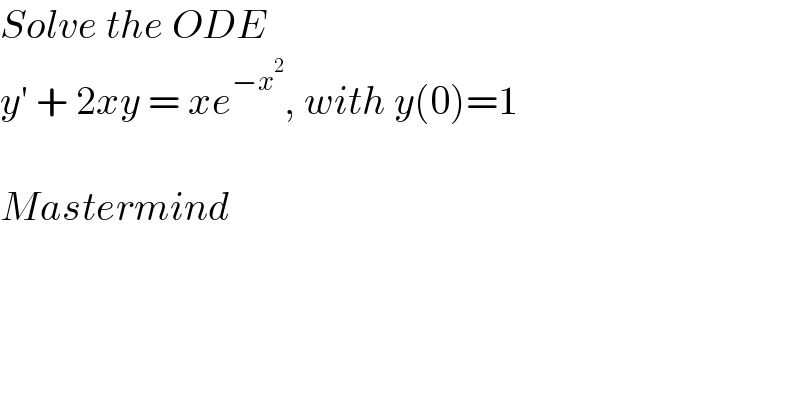
Solve the ODE y′ + 2xy = xe^(−x^2 ) , with y(0)=1 Mastermind

$${Solve}\:{the}\:{ODE}\: \\ $$$${y}'\:+\:\mathrm{2}{xy}\:=\:{xe}^{−{x}^{\mathrm{2}} } ,\:{with}\:{y}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$ \\ $$$${Mastermind} \\ $$

Answered by haladu last updated on 23/Apr/22

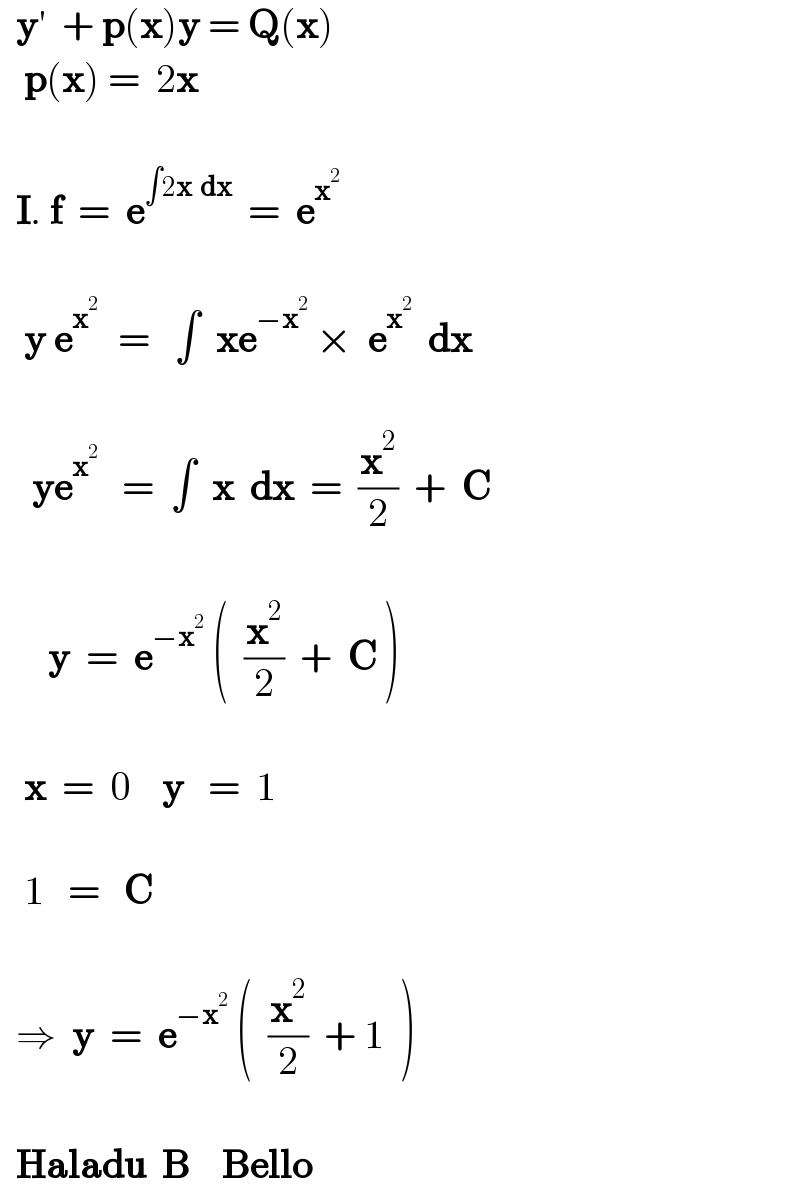
y′ + p(x)y = Q(x) p(x) = 2x I. f = e^(∫2x dx) = e^(x^2 ) y e^(x^2 ) = ∫ xe^(−x^2 ) × e^x^2 dx ye^x^2 = ∫ x dx = (x^2 /2) + C y = e^(−x^2 ) ( (x^2 /2) + C ) x = 0 y = 1 1 = C ⇒ y = e^(−x^2 ) ( (x^2 /2) + 1 ) Haladu B Bello

$$\:\:\boldsymbol{\mathrm{y}}'\:\:+\:\boldsymbol{\mathrm{p}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{y}}\:=\:\boldsymbol{\mathrm{Q}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\:\:\:\boldsymbol{\mathrm{p}}\left(\boldsymbol{\mathrm{x}}\right)\:=\:\:\mathrm{2}\boldsymbol{\mathrm{x}}\:\: \\ $$$$\:\: \\ $$$$\:\:\boldsymbol{\mathrm{I}}.\:\boldsymbol{\mathrm{f}}\:\:=\:\:\boldsymbol{\mathrm{e}}^{\int\mathrm{2}\boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{dx}}} \:\:=\:\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:} \:\: \\ $$$$\:\:\: \\ $$$$\:\:\:\boldsymbol{\mathrm{y}}\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:} \:\:=\:\:\:\int\:\:\boldsymbol{\mathrm{xe}}^{−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:×\:\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\:\boldsymbol{\mathrm{dx}}\:\: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\boldsymbol{\mathrm{ye}}^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\:\:=\:\:\int\:\:\boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{dx}}\:\:=\:\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{2}}\:\:+\:\:\boldsymbol{\mathrm{C}} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\boldsymbol{\mathrm{y}}\:\:=\:\:\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\left(\:\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{2}}\:\:+\:\:\boldsymbol{\mathrm{C}}\:\right) \\ $$$$\:\:\: \\ $$$$\:\:\:\boldsymbol{\mathrm{x}}\:\:=\:\:\mathrm{0}\:\:\:\:\boldsymbol{\mathrm{y}}\:\:\:=\:\:\mathrm{1}\:\: \\ $$$$\:\:\: \\ $$$$\:\:\:\mathrm{1}\:\:\:=\:\:\:\boldsymbol{\mathrm{C}} \\ $$$$\:\: \\ $$$$\:\:\Rightarrow\:\:\boldsymbol{\mathrm{y}}\:\:=\:\:\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \:\left(\:\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{2}}\:\:+\:\mathrm{1}\:\:\right) \\ $$$$\:\:\: \\ $$$$\:\:\boldsymbol{\mathrm{Haladu}}\:\:\boldsymbol{\mathrm{B}}\:\:\:\:\boldsymbol{\mathrm{Bello}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com