
Question Number 169073 by MikeH last updated on 23/Apr/22
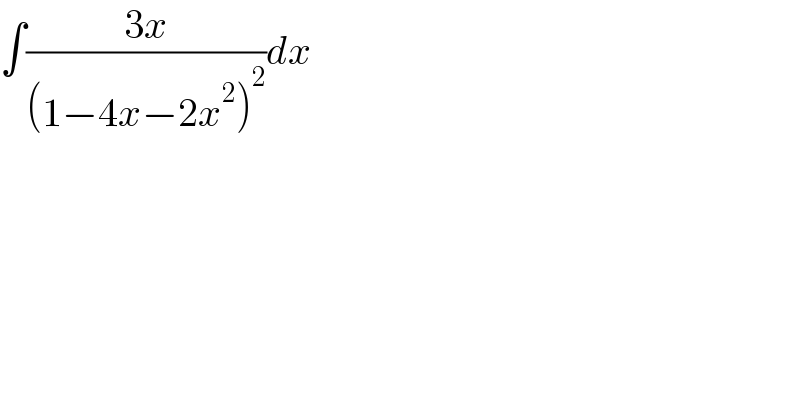
$$\int\frac{\mathrm{3}{x}}{\left(\mathrm{1}−\mathrm{4}{x}−\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$
Answered by MJS_new last updated on 24/Apr/22
![∫((3x)/((2x^2 +4x−1)^2 ))dx= [Ostrogradski′s Method] =((2x−1)/(4(2x^2 +4x−1)))+(1/2)∫(dx/(2x^2 +4x−1))= =((2x−1)/(4(2x^2 +4x−1)))+((√6)/(12))∫((1/(2x+2−(√6)))−(1/(2x+2+(√6))))dx= =((2x−1)/(4(2x^2 +4x−1)))+((√6)/(24))ln ∣((2x+2−(√6))/(2x+2+(√6)))∣ +C](Q169124.png)
$$\int\frac{\mathrm{3}{x}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}}= \\ $$$$=\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}\right)}+\frac{\sqrt{\mathrm{6}}}{\mathrm{12}}\int\left(\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}−\sqrt{\mathrm{6}}}−\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{2}+\sqrt{\mathrm{6}}}\right){dx}= \\ $$$$=\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}\right)}+\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{ln}\:\mid\frac{\mathrm{2}{x}+\mathrm{2}−\sqrt{\mathrm{6}}}{\mathrm{2}{x}+\mathrm{2}+\sqrt{\mathrm{6}}}\mid\:+{C} \\ $$
Commented by MikeH last updated on 24/Apr/22
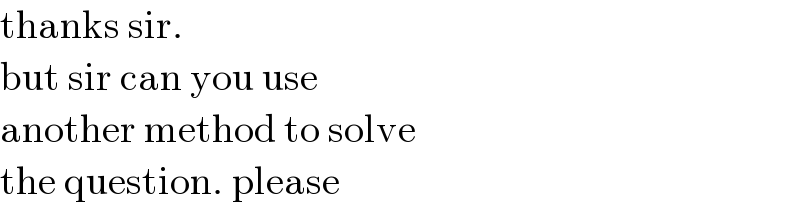
$$\mathrm{thanks}\:\mathrm{sir}.\: \\ $$$$\mathrm{but}\:\mathrm{sir}\:\mathrm{can}\:\mathrm{you}\:\mathrm{use} \\ $$$$\mathrm{another}\:\mathrm{method}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{the}\:\mathrm{question}.\:\mathrm{please} \\ $$
Commented by SLVR last updated on 25/Apr/22
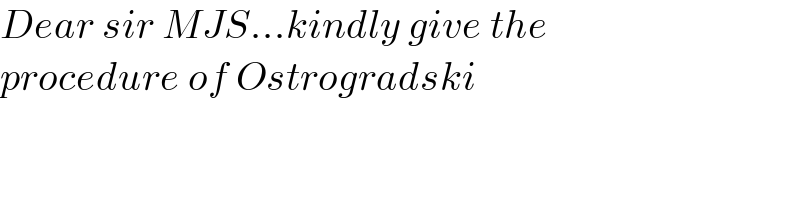
$${Dear}\:{sir}\:{MJS}...{kindly}\:{give}\:{the} \\ $$$${procedure}\:{of}\:{Ostrogradski} \\ $$
Answered by MJS_new last updated on 24/Apr/22
![3∫(x/((2x^2 +4x−1)^2 ))dx= [t=(((√6)(x+1))/3) → dx=((√6)/2)dt] =(1/6)∫((3t−(√6))/((t^2 −1)^2 ))dt= =−((√6)/(24))∫(dt/(t+1))−((3+(√6))/(24))∫(dt/((t+1)^2 ))+((√6)/(24))∫(dt/(t−1))+((3−(√6))/(24))∫(dt/((t^2 −1)^2 ))= =−((√6)/(24))ln (t+1) +((3+(√6))/(24(t+1)))+((√6)/(24))ln (t−1) −((3−(√6))/(24(t−1)))= =((√6)/(24))ln ((t−1)/(t+1)) +(((√6)t−3)/(12(t^2 −1)))= =((√6)/(24))ln ∣((2x+2−(√6))/(2x+2+(√6)))∣ +((2x−1)/(4(2x^2 +4x−1)))+C](Q169144.png)
$$\mathrm{3}\int\frac{{x}}{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{6}}\left({x}+\mathrm{1}\right)}{\mathrm{3}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{3}{t}−\sqrt{\mathrm{6}}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$=−\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{3}+\sqrt{\mathrm{6}}}{\mathrm{24}}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\int\frac{{dt}}{{t}−\mathrm{1}}+\frac{\mathrm{3}−\sqrt{\mathrm{6}}}{\mathrm{24}}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=−\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:+\frac{\mathrm{3}+\sqrt{\mathrm{6}}}{\mathrm{24}\left({t}+\mathrm{1}\right)}+\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:−\frac{\mathrm{3}−\sqrt{\mathrm{6}}}{\mathrm{24}\left({t}−\mathrm{1}\right)}= \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{ln}\:\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\:+\frac{\sqrt{\mathrm{6}}{t}−\mathrm{3}}{\mathrm{12}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}= \\ $$$$=\frac{\sqrt{\mathrm{6}}}{\mathrm{24}}\mathrm{ln}\:\mid\frac{\mathrm{2}{x}+\mathrm{2}−\sqrt{\mathrm{6}}}{\mathrm{2}{x}+\mathrm{2}+\sqrt{\mathrm{6}}}\mid\:+\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{1}\right)}+{C} \\ $$
Commented by MikeH last updated on 25/Apr/22

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
