Math Question and Answers


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 169117 by infinityaction last updated on 24/Apr/22

	Answered by greougoury555 last updated on 24/Apr/22
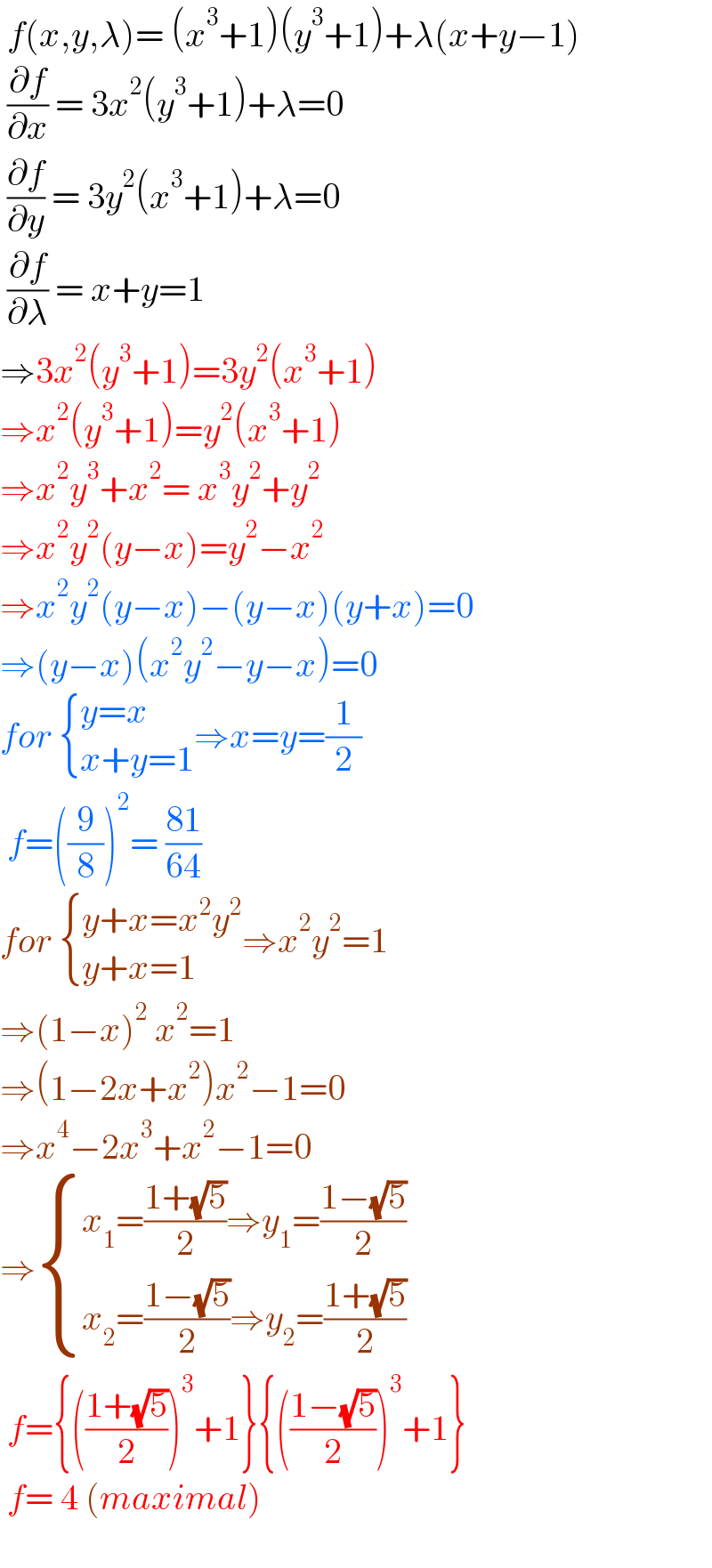
	$f(x,y,λ)= (x^3 +1)(y^3 +1)+λ(x+y−1) (∂f/∂x) = 3x^2 (y^3 +1)+λ=0 (∂f/∂y) = 3y^2 (x^3 +1)+λ=0 (∂f/∂λ) = x+y=1 ⇒3x^2 (y^3 +1)=3y^2 (x^3 +1) ⇒x^2 (y^3 +1)=y^2 (x^3 +1) ⇒x^2 y^3 +x^2 = x^3 y^2 +y^2 ⇒x^2 y^2 (y−x)=y^2 −x^2 ⇒x^2 y^2 (y−x)−(y−x)(y+x)=0 ⇒(y−x)(x^2 y^2 −y−x)=0 for { ((y=x)),((x+y=1)) :}⇒x=y=(1/2) f=((9/8))^2 = ((81)/(64)) for { ((y+x=x^2 y^2 )),((y+x=1)) :}⇒x^2 y^2 =1 ⇒(1−x)^2 x^2 =1 ⇒(1−2x+x^2 )x^2 −1=0 ⇒x^4 −2x^3 +x^2 −1=0 ⇒ { ((x_1 =((1+(√5))/2)⇒y_1 =((1−(√5))/2))),((x_2 =((1−(√5))/2)⇒y_2 =((1+(√5))/2))) :} f={(((1+(√5))/2))^3 +1}{(((1−(√5))/2))^3 +1} f= 4 (maximal)$
	$f (x, y, λ) = (x^{3} + 1) (y^{3} + 1) + λ (x + y - 1)$ $\frac{\partial f}{\partial x} = 3 x^{2} (y^{3} + 1) + λ = 0$ $\frac{\partial f}{\partial y} = 3 y^{2} (x^{3} + 1) + λ = 0$ $\frac{\partial f}{\partial λ} = x + y = 1$ $\Rightarrow 3 x^{2} (y^{3} + 1) = 3 y^{2} (x^{3} + 1)$ $\Rightarrow x^{2} (y^{3} + 1) = y^{2} (x^{3} + 1)$ $\Rightarrow x^{2} y^{3} + x^{2} = x^{3} y^{2} + y^{2}$ $\Rightarrow x^{2} y^{2} (y - x) = y^{2} - x^{2}$ $\Rightarrow x^{2} y^{2} (y - x) - (y - x) (y + x) = 0$ $\Rightarrow (y - x) (x^{2} y^{2} - y - x) = 0$ $f o r {\begin{cases} y = x \\ x + y = 1 \end{cases} \Rightarrow x = y = \frac{1}{2}$ $f = {(\frac{9}{8})}^{2} = \frac{81}{64}$ $f o r {\begin{cases} y + x = x^{2} y^{2} \\ y + x = 1 \end{cases} \Rightarrow x^{2} y^{2} = 1$ $\Rightarrow {(1 - x)}^{2} x^{2} = 1$ $\Rightarrow (1 - 2 x + x^{2}) x^{2} - 1 = 0$ $\Rightarrow x^{4} - 2 x^{3} + x^{2} - 1 = 0$ $\Rightarrow {\begin{cases} x_{1} = \frac{1 + \sqrt{5}}{2} \Rightarrow y_{1} = \frac{1 - \sqrt{5}}{2} \\ x_{2} = \frac{1 - \sqrt{5}}{2} \Rightarrow y_{2} = \frac{1 + \sqrt{5}}{2} \end{cases}$ $f = {{(\frac{1 + \sqrt{5}}{2})}^{3} + 1} {{(\frac{1 - \sqrt{5}}{2})}^{3} + 1}$ $f = 4 (m a x i m a l)$
	Commented by infinityaction last updated on 24/Apr/22

	$t h a n k y o u s i r$
	Commented by tahish last updated on 24/Apr/22
	sir muje new image updolad krani ho to kaiser kare
	Commented by infinityaction last updated on 26/Apr/22

	$m e r i t a l e g r a m i d @ i n f i n i t y_a c t i o n$ $h a i a a p v a h a p r p u c c h e$
	Answered by MJS_new last updated on 24/Apr/22

	$y = 1 - x$ $\Rightarrow$ $f (x) = (x^{3} + 1) \times (y^{3} + 1) = (x^{3} + 1) \times ({(1 - x)}^{3} + 1) =$ $= (x^{2} - x + 1) (x + 1) \times (x^{2} - x + 1) (2 - x) =$ $= - (x - 2) (x + 1) {(x^{2} - x + 1)}^{2}$ $f^{'} (x) = 0$ $- 3 (2 x - 1) (x^{2} - x - 1) (x^{2} - x + 1) = 0$ $x_{1} = \frac{1}{2} - \frac{\sqrt{5}}{2}; f (x_{1}) = 4$ $x_{2} = \frac{1}{2}; f (x_{2}) = \frac{81}{64}$ $x_{3} = \frac{1}{2} + \frac{\sqrt{5}}{2}; f (x_{3}) = 4$ $\max value is 4$
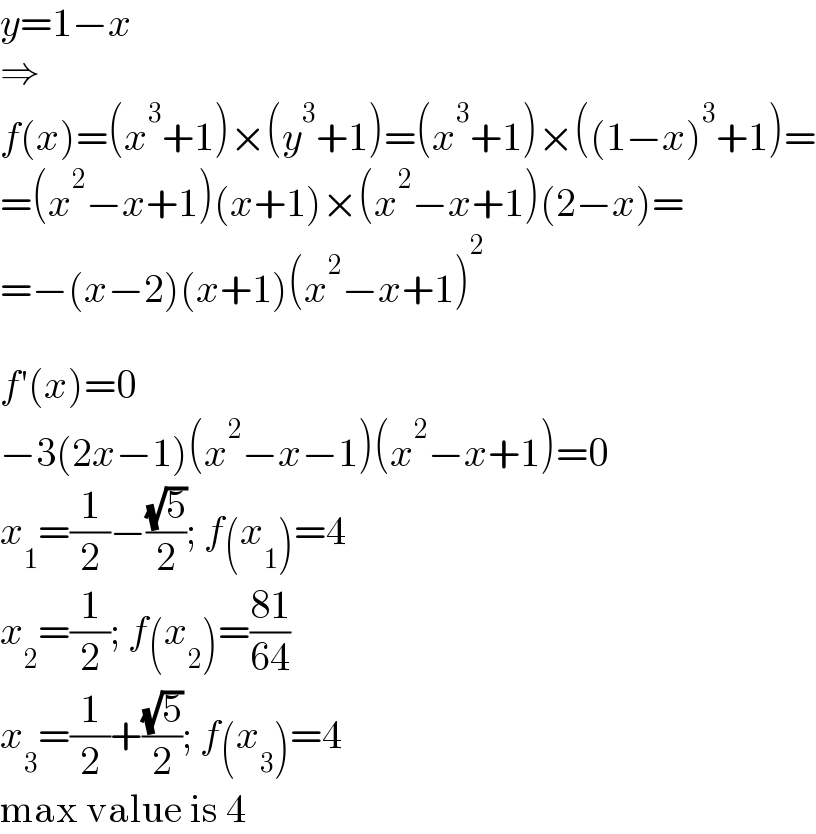
	Commented by infinityaction last updated on 24/Apr/22

	$t h a n k y o u s i r$
	Answered by mr W last updated on 24/Apr/22

	$S = (x^{3} + 1) (y^{3} + 1)$ $= 1 + {(x y)}^{3} + x^{3} + y^{3}$ $= 1 + {(x y)}^{3} + {(x + y)}^{3} - 3 x y (x + y)$ $= 1 + {(x y)}^{3} + 1 - 3 x y$ $= {(x y)}^{3} - 3 (x y) + 2$ ${(x y)}^{3} - 3 (x y) + 2 - S = 0$ $Δ = {(- 1)}^{3} + {(1 - \frac{S}{2})}^{2} ⩽ 0$ $- 1 ⩽ 1 - \frac{S}{2} ⩽ 1$ $0 ⩽ S ⩽ 4 \Rightarrow S_{m a x} = 4$
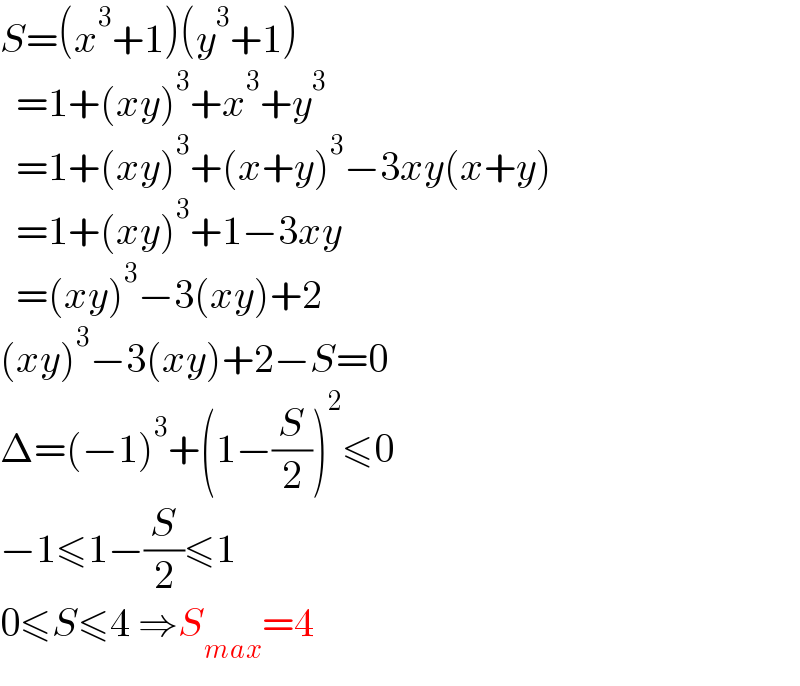
	Commented by infinityaction last updated on 25/Apr/22

	$t h a n k y o u s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum