
Question and Answers Forum
Question Number 169164 by 0731619 last updated on 25/Apr/22

Commented by infinityaction last updated on 25/Apr/22

Commented by infinityaction last updated on 25/Apr/22
![let p = ((x^2 +3x)/((x+1)(x^2 +1))) p = (((x+1)^2 +(x−1))/((x+1)(x^2 +1))) p = ((x+1)/(x^2 +1)) + ((x−1)/((x+1)(x^2 +1))) p = ((x+1)/(x^2 +1)) − (((x^2 +1)−x(x+1))/((x+1)(x^2 +1))) p = ((x+1)/(x^2 +1)) − (1/(x+1)) +(x/(x^2 +1)) p = ((2x)/(x^2 +1))+(1/(x^2 +1)) − (1/(x+1)) I = ∫_0 ^1 {((2x)/(x^2 +1))+(1/(x^2 +1))−(1/(x+1))}dx I = [log (x^2 +1) + tan^(−1) (x) + log (x+1)]_0 ^1 I = log 2 + (π/4) + log 2 I = (π/4) + log 4](Q169167.png)
Answered by Mathspace last updated on 25/Apr/22
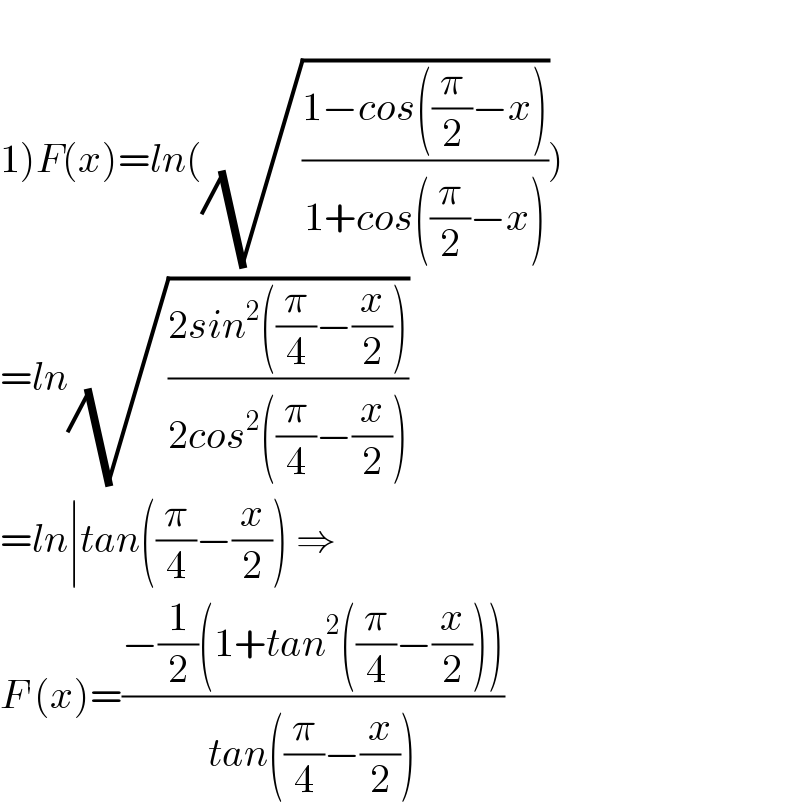
| ||
Question and Answers Forum | ||
Question Number 169164 by 0731619 last updated on 25/Apr/22 | ||
 | ||
Commented by infinityaction last updated on 25/Apr/22 | ||
 | ||
Commented by infinityaction last updated on 25/Apr/22 | ||
![let p = ((x^2 +3x)/((x+1)(x^2 +1))) p = (((x+1)^2 +(x−1))/((x+1)(x^2 +1))) p = ((x+1)/(x^2 +1)) + ((x−1)/((x+1)(x^2 +1))) p = ((x+1)/(x^2 +1)) − (((x^2 +1)−x(x+1))/((x+1)(x^2 +1))) p = ((x+1)/(x^2 +1)) − (1/(x+1)) +(x/(x^2 +1)) p = ((2x)/(x^2 +1))+(1/(x^2 +1)) − (1/(x+1)) I = ∫_0 ^1 {((2x)/(x^2 +1))+(1/(x^2 +1))−(1/(x+1))}dx I = [log (x^2 +1) + tan^(−1) (x) + log (x+1)]_0 ^1 I = log 2 + (π/4) + log 2 I = (π/4) + log 4](Q169167.png) | ||
Answered by Mathspace last updated on 25/Apr/22 | ||
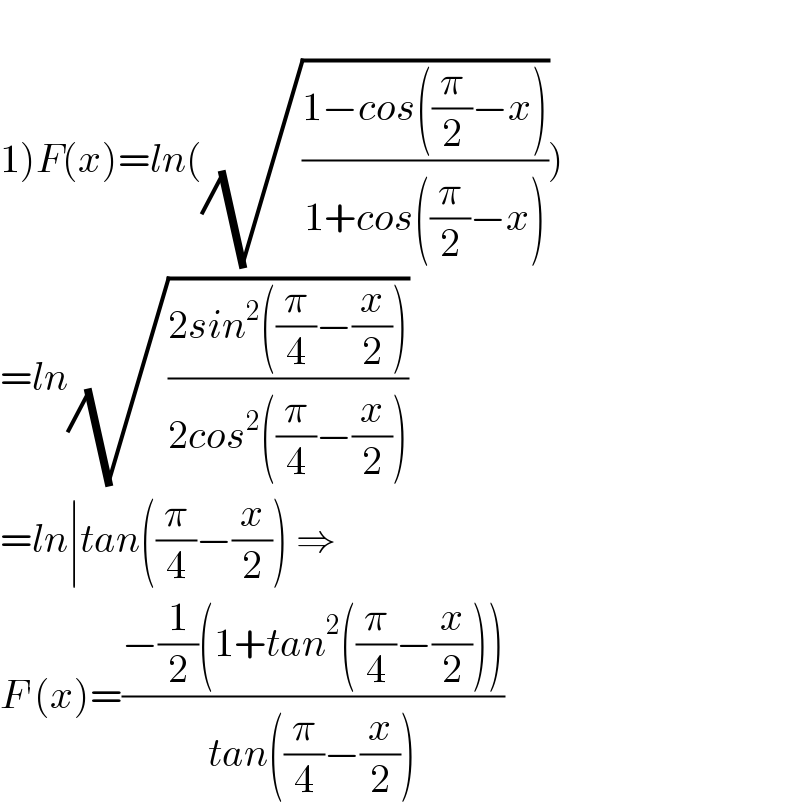 | ||
| ||