Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 169166 by infinityaction last updated on 25/Apr/22

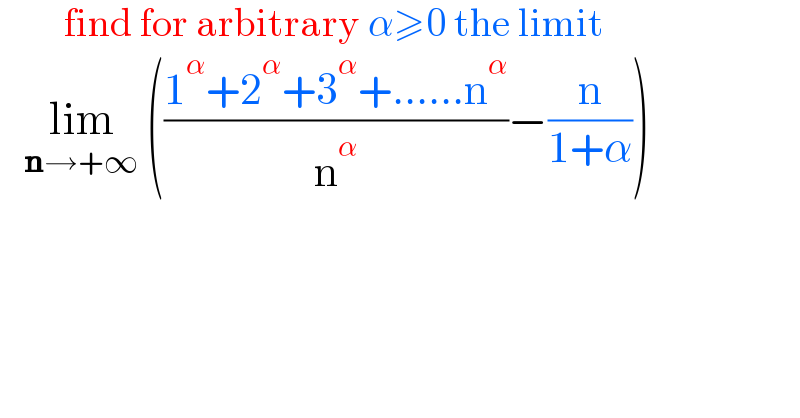
find for arbitrary α≥0 the limit lim_(n→+∞) (((1^α +2^α +3^α +......n^α )/n^α )−(n/(1+α)))

$$\:\:\:\:\:\:\:\:\mathrm{find}\:\mathrm{for}\:\mathrm{arbitrary}\:\alpha\geqslant\mathrm{0}\:\mathrm{the}\:\mathrm{limit}\: \\ $$$$\:\:\:\underset{\boldsymbol{\mathrm{n}}\rightarrow+\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}^{\alpha} +\mathrm{2}^{\alpha} +\mathrm{3}^{\alpha} +......\mathrm{n}^{\alpha} }{\mathrm{n}^{\alpha} }−\frac{\mathrm{n}}{\mathrm{1}+\alpha}\right) \\ $$

Commented by safojontoshtemirov last updated on 25/Apr/22

(1/2)

$$\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by infinityaction last updated on 25/Apr/22

sir solution

$${sir}\:{solution} \\ $$

Commented by infinityaction last updated on 25/Apr/22

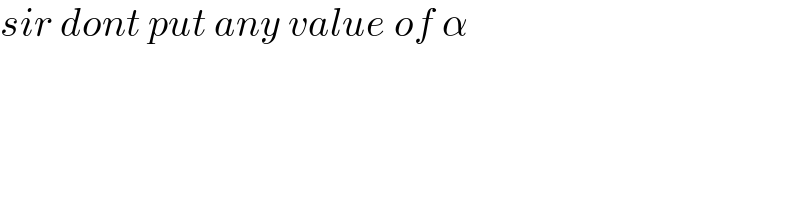
sir dont put any value of α

$${sir}\:{dont}\:{put}\:{any}\:{value}\:{of}\:\alpha \\ $$

Commented by infinityaction last updated on 25/Apr/22

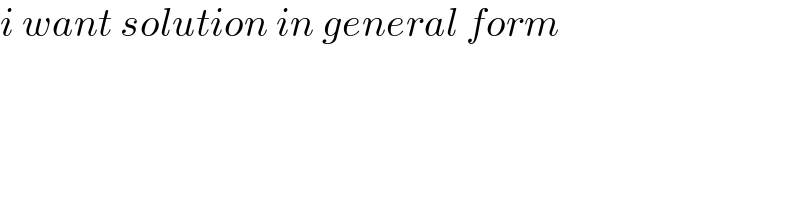
i want solution in general form

$${i}\:{want}\:{solution}\:{in}\:{general}\:{form} \\ $$

Answered by aleks041103 last updated on 25/Apr/22

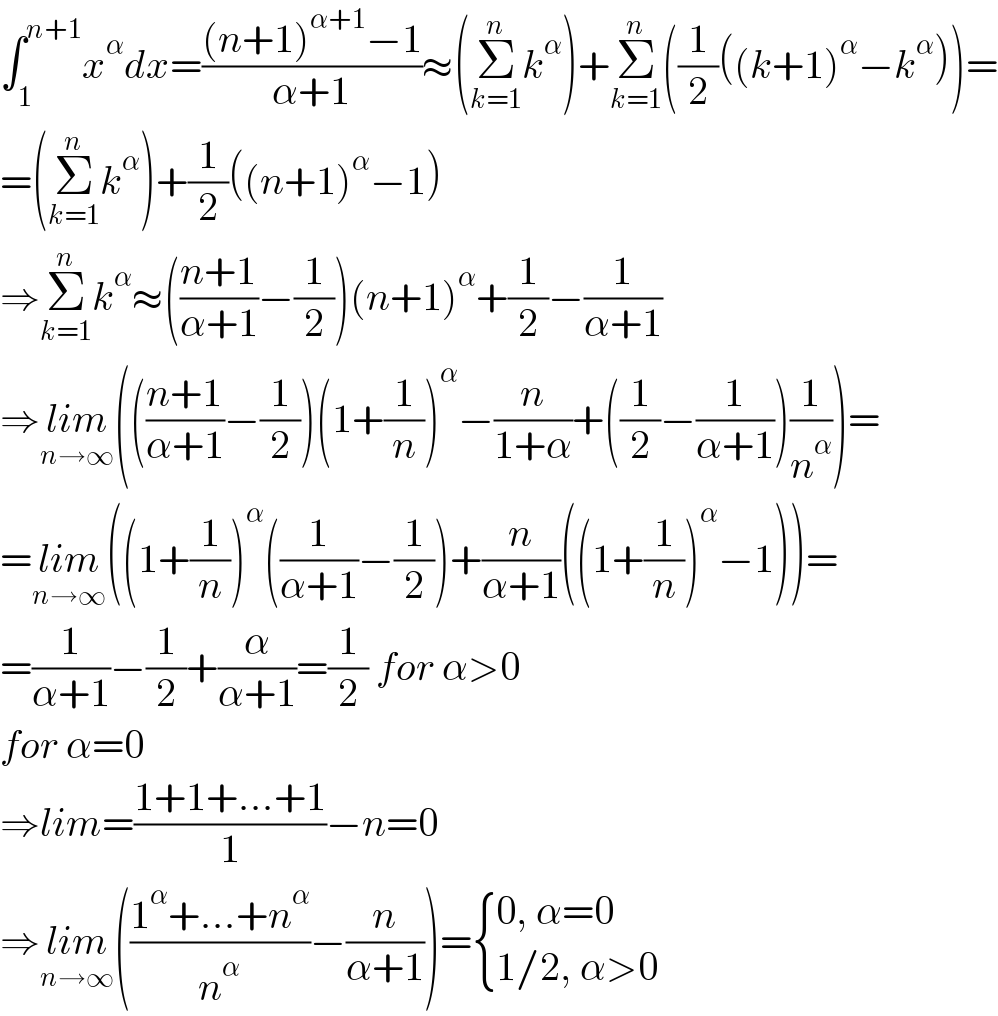
∫_1 ^(n+1) x^α dx=(((n+1)^(α+1) −1)/(α+1))≈(Σ_(k=1) ^n k^α )+Σ_(k=1) ^n ((1/2)((k+1)^α −k^α ))= =(Σ_(k=1) ^n k^α )+(1/2)((n+1)^α −1) ⇒Σ_(k=1) ^n k^α ≈(((n+1)/(α+1))−(1/2))(n+1)^α +(1/2)−(1/(α+1)) ⇒lim_(n→∞) ((((n+1)/(α+1))−(1/2))(1+(1/n))^α −(n/(1+α))+((1/2)−(1/(α+1)))(1/n^α ))= =lim_(n→∞) ((1+(1/n))^α ((1/(α+1))−(1/2))+(n/(α+1))((1+(1/n))^α −1))= =(1/(α+1))−(1/2)+(α/(α+1))=(1/2) for α>0 for α=0 ⇒lim=((1+1+...+1)/1)−n=0 ⇒lim_(n→∞) (((1^α +...+n^α )/n^α )−(n/(α+1)))= { ((0, α=0)),((1/2, α>0)) :}

$$\int_{\mathrm{1}} ^{{n}+\mathrm{1}} {x}^{\alpha} {dx}=\frac{\left({n}+\mathrm{1}\right)^{\alpha+\mathrm{1}} −\mathrm{1}}{\alpha+\mathrm{1}}\approx\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\alpha} \right)+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\left({k}+\mathrm{1}\right)^{\alpha} −{k}^{\alpha} \right)\right)= \\ $$$$=\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\alpha} \right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\left({n}+\mathrm{1}\right)^{\alpha} −\mathrm{1}\right) \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\alpha} \approx\left(\frac{{n}+\mathrm{1}}{\alpha+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({n}+\mathrm{1}\right)^{\alpha} +\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\alpha+\mathrm{1}} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {{lim}}\left(\left(\frac{{n}+\mathrm{1}}{\alpha+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\alpha} −\frac{{n}}{\mathrm{1}+\alpha}+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\alpha+\mathrm{1}}\right)\frac{\mathrm{1}}{{n}^{\alpha} }\right)= \\ $$$$=\underset{{n}\rightarrow\infty} {{lim}}\left(\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\alpha} \left(\frac{\mathrm{1}}{\alpha+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{{n}}{\alpha+\mathrm{1}}\left(\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\alpha} −\mathrm{1}\right)\right)= \\ $$$$=\frac{\mathrm{1}}{\alpha+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\alpha}{\alpha+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\:{for}\:\alpha>\mathrm{0} \\ $$$${for}\:\alpha=\mathrm{0} \\ $$$$\Rightarrow{lim}=\frac{\mathrm{1}+\mathrm{1}+...+\mathrm{1}}{\mathrm{1}}−{n}=\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {{lim}}\left(\frac{\mathrm{1}^{\alpha} +...+{n}^{\alpha} }{{n}^{\alpha} }−\frac{{n}}{\alpha+\mathrm{1}}\right)=\begin{cases}{\mathrm{0},\:\alpha=\mathrm{0}}\\{\mathrm{1}/\mathrm{2},\:\alpha>\mathrm{0}}\end{cases} \\ $$

Commented by infinityaction last updated on 25/Apr/22

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com