Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 169396 by Mastermind last updated on 29/Apr/22

(√x)+1=0 find x Mastermind

$$\sqrt{{x}}+\mathrm{1}=\mathrm{0} \\ $$$${find}\:{x} \\ $$$$ \\ $$$${Mastermind} \\ $$

Commented by mr W last updated on 29/Apr/22

i^4 =1 (√i^4 )+1=2≠0

$${i}^{\mathrm{4}} =\mathrm{1} \\ $$$$\sqrt{{i}^{\mathrm{4}} }+\mathrm{1}=\mathrm{2}\neq\mathrm{0} \\ $$

Commented by infinityaction last updated on 29/Apr/22

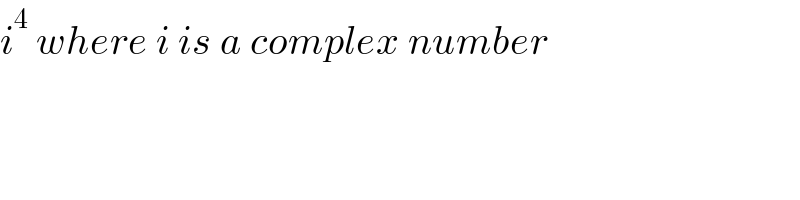
i^4 where i is a complex number

$${i}^{\mathrm{4}} \:{where}\:{i}\:{is}\:{a}\:{complex}\:{number} \\ $$

Commented by mr W last updated on 29/Apr/22

(√x)+1=0 has no solution even for x∈C.

$$\sqrt{{x}}+\mathrm{1}=\mathrm{0}\:{has}\:{no}\:{solution}\:{even}\:{for} \\ $$$${x}\in\mathbb{C}. \\ $$

Commented by Mastermind last updated on 29/Apr/22

Wow! thanks man

$${Wow}! \\ $$$${thanks}\:{man} \\ $$

Commented by Mastermind last updated on 29/Apr/22

i love the way you answered it

$${i}\:{love}\:{the}\:{way}\:{you}\:{answered}\:{it} \\ $$

Commented by Mastermind last updated on 29/Apr/22

Thank you too, for attempting it

$${Thank}\:{you}\:{too},\:{for}\:{attempting}\:{it} \\ $$

Commented by Mastermind last updated on 29/Apr/22

But why didn′t you consider law of exponential (√((x^n )))=x^(n/2) Now, x=i^4 (√((i^4 )))=i^(4/2) ⇒i^2 =−1 I want you to check this @mr W

$${But}\:{why}\:{didn}'{t}\:{you}\:{consider}\:{law}\:{of} \\ $$$${exponential} \\ $$$$\sqrt{\left({x}^{{n}} \right)}={x}^{\frac{{n}}{\mathrm{2}}} \\ $$$${Now},\:{x}={i}^{\mathrm{4}} \\ $$$$\sqrt{\left({i}^{\mathrm{4}} \right)}={i}^{\frac{\mathrm{4}}{\mathrm{2}}} \Rightarrow{i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$ \\ $$$${I}\:{want}\:{you}\:{to}\:{check}\:{this}\:@{mr}\:{W} \\ $$

Commented by mr W last updated on 30/Apr/22

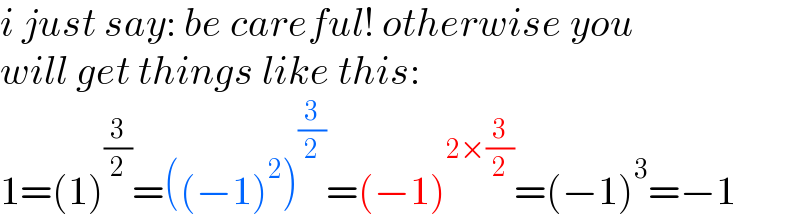
i just say: be careful! otherwise you will get things like this: 1=(1)^(3/2) =((−1)^2 )^(3/2) =(−1)^(2×(3/2)) =(−1)^3 =−1

$${i}\:{just}\:{say}:\:{be}\:{careful}!\:{otherwise}\:{you} \\ $$$${will}\:{get}\:{things}\:{like}\:{this}: \\ $$$$\mathrm{1}=\left(\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\left(\left(−\mathrm{1}\right)^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} =\left(−\mathrm{1}\right)^{\mathrm{2}×\frac{\mathrm{3}}{\mathrm{2}}} =\left(−\mathrm{1}\right)^{\mathrm{3}} =−\mathrm{1} \\ $$

Commented by infinityaction last updated on 30/Apr/22

i^4 = 1 (√x) = −1 i^2 = −1 (√x) = i^2 x = i^4

$${i}^{\mathrm{4}} \:=\:\mathrm{1}\: \\ $$$$\sqrt{{x}}\:=\:−\mathrm{1} \\ $$$${i}^{\mathrm{2}} \:\:=\:−\mathrm{1} \\ $$$$\sqrt{{x}}\:=\:{i}^{\mathrm{2}} \\ $$$${x}\:=\:{i}^{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$

Commented by mr W last updated on 30/Apr/22

(√x)=i^2 ⇎x=i^4 be careful again! when you square an equation, you get a new equation which may contain roots which are not the roots of the original equation. so you must check if the roots fulfill the original equation. in current case you′ll see that x=i^4 doesn′t fulfill the original equation.

$$\sqrt{{x}}={i}^{\mathrm{2}} \nLeftrightarrow{x}={i}^{\mathrm{4}} \\ $$$${be}\:{careful}\:{again}! \\ $$$${when}\:{you}\:{square}\:{an}\:{equation},\:{you} \\ $$$${get}\:{a}\:{new}\:{equation}\:{which}\:{may}\:{contain}\: \\ $$$${roots}\:{which}\:{are}\:{not}\:{the}\:{roots}\:{of}\:{the}\: \\ $$$${original}\:{equation}.\:{so}\:{you}\:{must}\:{check} \\ $$$${if}\:{the}\:{roots}\:{fulfill}\:{the}\:{original} \\ $$$${equation}.\:{in}\:{current}\:{case}\:{you}'{ll}\:{see} \\ $$$${that}\:{x}={i}^{\mathrm{4}} \:{doesn}'{t}\:{fulfill}\:{the}\:{original} \\ $$$${equation}. \\ $$

Commented by mr W last updated on 30/Apr/22

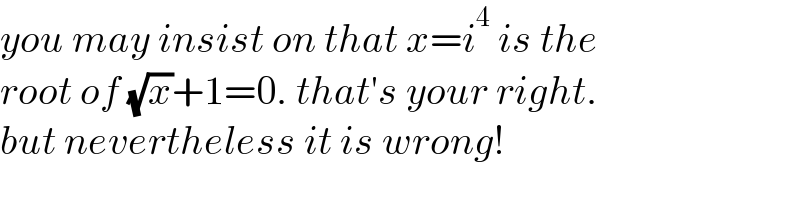
you may insist on that x=i^4 is the root of (√x)+1=0. that′s your right. but nevertheless it is wrong!

$${you}\:{may}\:{insist}\:{on}\:{that}\:{x}={i}^{\mathrm{4}} \:{is}\:{the} \\ $$$${root}\:{of}\:\sqrt{{x}}+\mathrm{1}=\mathrm{0}.\:{that}'{s}\:{your}\:{right}. \\ $$$${but}\:{nevertheless}\:{it}\:{is}\:{wrong}! \\ $$

Commented by mr W last updated on 30/Apr/22

Commented by infinityaction last updated on 30/Apr/22

got it sir thank you sir

$${got}\:{it}\:{sir} \\ $$$${thank}\:{you}\:{sir} \\ $$

Commented by MJS_new last updated on 30/Apr/22

steps we use to solve i.e. x^3 =−1; x∈C x^3 =e^(iπ) we must search for x=e^(iθ) with e^(3iθ) =e^(iπ) ⇒ 3θ=π ⇔ θ=(π/3) ⇒ x=e^(i(π/3)) =−(1/2)+((√3)/2)i but there′s more: x_k ^3 =e^(i(π+2πn)) ; n=0, 1, 2∧k=n+1 this “trick” on the rhs leads to 3 solutions. we did nothing on the lhs x_1 ^3 =e^(iπ) ⇒ x_1 =e^(i(π/3)) =−(1/2)+((√3)/2)i x_2 ^3 =e^(3iπ) ⇒ x_2 =e^(iπ) =−1 x_3 ^3 =e^(5iπ) ⇒ x_3 =e^(i((5π)/3)) =−(1/2)−((√3)/2)i tbese 3 solutions represent 3 different points in the complex plane now test the solutions (e^(i(π/3)) )^3 =e^(iπ) =−1 true (e^(iπ) )^3 =e^(3iπ) =e^(iπ) =−1 true (e^(i((5π)/3)) )^3 =e^(5iπ) =e^(iπ) =−1 true now let′s try x^(1/3) =−1; x∈C x^(1/3) =e^(iπ) obviously our ”trick” on the rhs doesn′t work (n∈N because we need a countable number of solutions) we must search for x=e^(iθ) with e^(i(θ/3)) =e^(iπ) ⇒ (θ/3)=π ⇔ θ=3π ⇒ x=e^(3iπ) =e^(iπ) =−1 but here we did something on the lhs test: (e^(iπ) )^(1/3) =e^(i(π/3)) ≠−1 so here′s a totally different case the rule x^(1/3) =−(−x)^(1/3) is only valid for x∈R strictly following the rules of C x^(1/3) =−1 has no solution now try x^(1/2) =−1; x∈C x^(1/2) =e^(iπ) x=e^(iθ) with e^(i(θ/2)) =e^(iπ) ⇒ (θ/2)=π ⇔ θ=2π ⇒ x=e^(2iπ) =e^(0iπ) =e^0 =1 again we did something on the lhs test: (e^0 )^(1/2) =e^0 =1≠−1 again no solution in C and obviously none in R (because (√1)=1; also f(x)=(√x) is only a half parabola) ⇒ we need a different approach for solving equations in C

$$\mathrm{steps}\:\mathrm{we}\:\mathrm{use}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{i}.\mathrm{e}. \\ $$$${x}^{\mathrm{3}} =−\mathrm{1};\:{x}\in\mathbb{C} \\ $$$${x}^{\mathrm{3}} =\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{search}\:\mathrm{for}\:{x}=\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:\mathrm{e}^{\mathrm{3i}\theta} =\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\Rightarrow\:\mathrm{3}\theta=\pi\:\Leftrightarrow\:\theta=\frac{\pi}{\mathrm{3}}\:\Rightarrow\:{x}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{but}\:\mathrm{there}'\mathrm{s}\:\mathrm{more}: \\ $$$${x}_{{k}} ^{\mathrm{3}} =\mathrm{e}^{\mathrm{i}\left(\pi+\mathrm{2}\pi{n}\right)} ;\:{n}=\mathrm{0},\:\mathrm{1},\:\mathrm{2}\wedge{k}={n}+\mathrm{1} \\ $$$$\mathrm{this}\:``\mathrm{trick}''\:\mathrm{on}\:\mathrm{the}\:\mathrm{rhs}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{3}\:\mathrm{solutions}. \\ $$$$\mathrm{we}\:\mathrm{did}\:\mathrm{nothing}\:\mathrm{on}\:\mathrm{the}\:\mathrm{lhs} \\ $$$${x}_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{e}^{\mathrm{i}\pi} \:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$${x}_{\mathrm{2}} ^{\mathrm{3}} =\mathrm{e}^{\mathrm{3i}\pi} \:\Rightarrow\:{x}_{\mathrm{2}} =\mathrm{e}^{\mathrm{i}\pi} =−\mathrm{1} \\ $$$${x}_{\mathrm{3}} ^{\mathrm{3}} =\mathrm{e}^{\mathrm{5i}\pi} \:\Rightarrow\:{x}_{\mathrm{3}} =\mathrm{e}^{\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{tbese}\:\mathrm{3}\:\mathrm{solutions}\:\mathrm{represent}\:\mathrm{3}\:\mathrm{different}\:\mathrm{points} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{plane} \\ $$$$\mathrm{now}\:\mathrm{test}\:\mathrm{the}\:\mathrm{solutions} \\ $$$$\left(\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} \right)^{\mathrm{3}} =\mathrm{e}^{\mathrm{i}\pi} =−\mathrm{1}\:\mathrm{true} \\ $$$$\left(\mathrm{e}^{\mathrm{i}\pi} \right)^{\mathrm{3}} =\mathrm{e}^{\mathrm{3i}\pi} =\mathrm{e}^{\mathrm{i}\pi} =−\mathrm{1}\:\mathrm{true} \\ $$$$\left(\mathrm{e}^{\mathrm{i}\frac{\mathrm{5}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} =\mathrm{e}^{\mathrm{5i}\pi} =\mathrm{e}^{\mathrm{i}\pi} =−\mathrm{1}\:\mathrm{true} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{let}'\mathrm{s}\:\mathrm{try} \\ $$$${x}^{\mathrm{1}/\mathrm{3}} =−\mathrm{1};\:{x}\in\mathbb{C} \\ $$$${x}^{\mathrm{1}/\mathrm{3}} =\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\mathrm{obviously}\:\mathrm{our}\:''\mathrm{trick}''\:\mathrm{on}\:\mathrm{the}\:\mathrm{rhs}\:\mathrm{doesn}'\mathrm{t} \\ $$$$\mathrm{work}\:\left({n}\in\mathbb{N}\:\mathrm{because}\:\mathrm{we}\:\mathrm{need}\:\mathrm{a}\:\mathrm{countable}\right. \\ $$$$\left.\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\right) \\ $$$$\mathrm{we}\:\mathrm{must}\:\mathrm{search}\:\mathrm{for}\:{x}=\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{3}}} =\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\Rightarrow\:\frac{\theta}{\mathrm{3}}=\pi\:\Leftrightarrow\:\theta=\mathrm{3}\pi\:\Rightarrow\:{x}=\mathrm{e}^{\mathrm{3i}\pi} =\mathrm{e}^{\mathrm{i}\pi} =−\mathrm{1} \\ $$$$\mathrm{but}\:\mathrm{here}\:\mathrm{we}\:\mathrm{did}\:\mathrm{something}\:\mathrm{on}\:\mathrm{the}\:\mathrm{lhs} \\ $$$$\mathrm{test}:\:\left(\mathrm{e}^{\mathrm{i}\pi} \right)^{\mathrm{1}/\mathrm{3}} =\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{3}}} \neq−\mathrm{1} \\ $$$$\mathrm{so}\:\mathrm{here}'\mathrm{s}\:\mathrm{a}\:\mathrm{totally}\:\mathrm{different}\:\mathrm{case} \\ $$$$\mathrm{the}\:\mathrm{rule}\:{x}^{\mathrm{1}/\mathrm{3}} =−\left(−{x}\right)^{\mathrm{1}/\mathrm{3}} \:\mathrm{is}\:\mathrm{only}\:\mathrm{valid}\:\mathrm{for}\:{x}\in\mathbb{R} \\ $$$$\mathrm{strictly}\:\mathrm{following}\:\mathrm{the}\:\mathrm{rules}\:\mathrm{of}\:\mathbb{C}\:{x}^{\mathrm{1}/\mathrm{3}} =−\mathrm{1}\:\mathrm{has} \\ $$$$\mathrm{no}\:\mathrm{solution} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{try} \\ $$$${x}^{\mathrm{1}/\mathrm{2}} =−\mathrm{1};\:{x}\in\mathbb{C} \\ $$$${x}^{\mathrm{1}/\mathrm{2}} =\mathrm{e}^{\mathrm{i}\pi} \\ $$$${x}=\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} =\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\Rightarrow\:\frac{\theta}{\mathrm{2}}=\pi\:\Leftrightarrow\:\theta=\mathrm{2}\pi\:\Rightarrow\:{x}=\mathrm{e}^{\mathrm{2i}\pi} =\mathrm{e}^{\mathrm{0i}\pi} =\mathrm{e}^{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{again}\:\mathrm{we}\:\mathrm{did}\:\mathrm{something}\:\mathrm{on}\:\mathrm{the}\:\mathrm{lhs} \\ $$$$\mathrm{test}:\:\left(\mathrm{e}^{\mathrm{0}} \right)^{\mathrm{1}/\mathrm{2}} =\mathrm{e}^{\mathrm{0}} =\mathrm{1}\neq−\mathrm{1} \\ $$$$\mathrm{again}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathbb{C}\:\mathrm{and}\:\mathrm{obviously}\:\mathrm{none} \\ $$$$\mathrm{in}\:\mathbb{R}\:\left(\mathrm{because}\:\sqrt{\mathrm{1}}=\mathrm{1};\:\mathrm{also}\:{f}\left({x}\right)=\sqrt{{x}}\:\mathrm{is}\:\mathrm{only}\right. \\ $$$$\left.\mathrm{a}\:\mathrm{half}\:\mathrm{parabola}\right) \\ $$$$ \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{need}\:\mathrm{a}\:\mathrm{different}\:\mathrm{approach}\:\mathrm{for}\:\mathrm{solving} \\ $$$$\mathrm{equations}\:\mathrm{in}\:\mathbb{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com