Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 169558 by greougoury555 last updated on 03/May/22

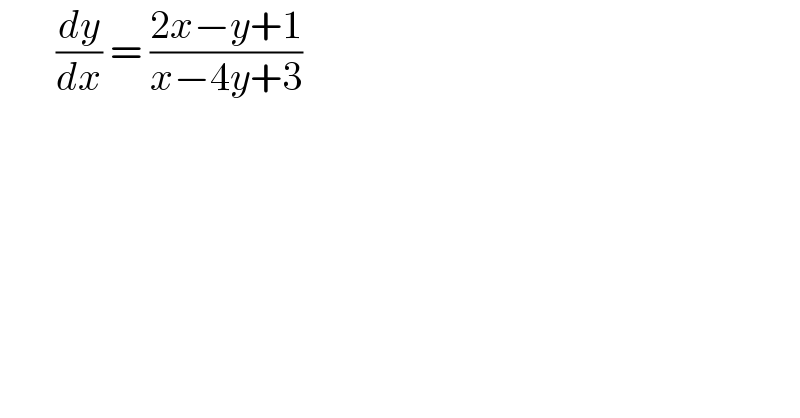
(dy/dx) = ((2x−y+1)/(x−4y+3))

$$\:\:\:\:\:\:\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}{x}−{y}+\mathrm{1}}{{x}−\mathrm{4}{y}+\mathrm{3}}\:\:\: \\ $$

Answered by ali009 last updated on 03/May/22

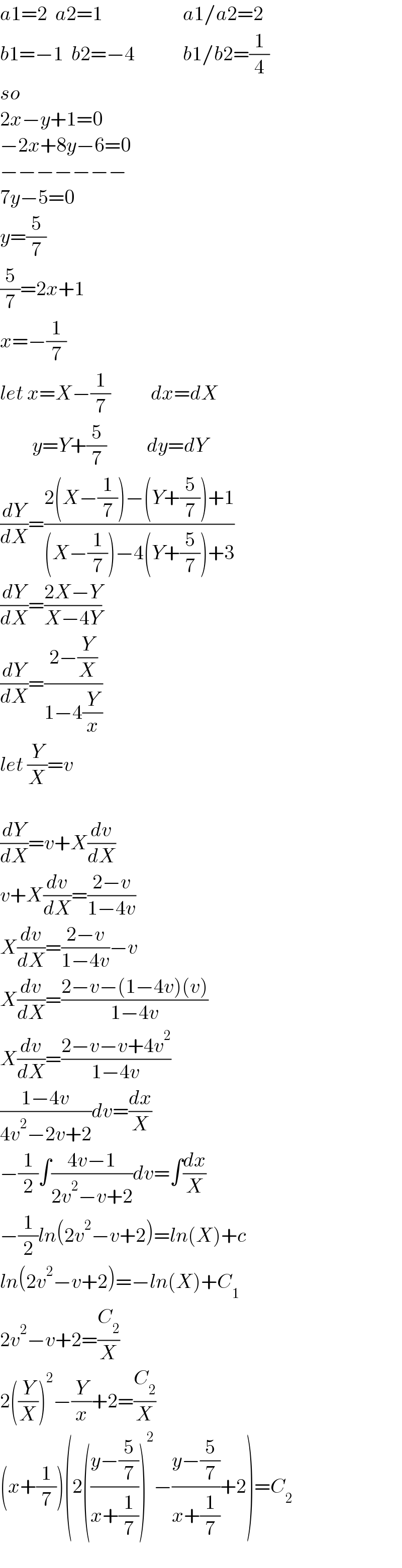
a1=2 a2=1 a1/a2=2 b1=−1 b2=−4 b1/b2=(1/4) so 2x−y+1=0 −2x+8y−6=0 −−−−−−− 7y−5=0 y=(5/7) (5/7)=2x+1 x=−(1/7) let x=X−(1/7) dx=dX y=Y+(5/7) dy=dY (dY/dX)=((2(X−(1/7))−(Y+(5/7))+1)/((X−(1/7))−4(Y+(5/7))+3)) (dY/dX)=((2X−Y)/(X−4Y)) (dY/dX)=((2−(Y/X))/(1−4(Y/x))) let (Y/X)=v (dY/dX)=v+X(dv/dX) v+X(dv/dX)=((2−v)/(1−4v)) X(dv/dX)=((2−v)/(1−4v))−v X(dv/dX)=((2−v−(1−4v)(v))/(1−4v)) X(dv/dX)=((2−v−v+4v^2 )/(1−4v)) ((1−4v)/(4v^2 −2v+2))dv=(dx/X) −(1/2)∫((4v−1)/(2v^2 −v+2))dv=∫(dx/X) −(1/2)ln(2v^2 −v+2)=ln(X)+c ln(2v^2 −v+2)=−ln(X)+C_1 2v^2 −v+2=(C_2 /X) 2((Y/X))^2 −(Y/x)+2=(C_2 /X) (x+(1/7))(2(((y−(5/7))/(x+(1/7))))^2 −((y−(5/7))/(x+(1/7)))+2)=C_2

$${a}\mathrm{1}=\mathrm{2}\:\:{a}\mathrm{2}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\mathrm{1}/{a}\mathrm{2}=\mathrm{2} \\ $$$${b}\mathrm{1}=−\mathrm{1}\:\:{b}\mathrm{2}=−\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:{b}\mathrm{1}/{b}\mathrm{2}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${so} \\ $$$$\mathrm{2}{x}−{y}+\mathrm{1}=\mathrm{0} \\ $$$$−\mathrm{2}{x}+\mathrm{8}{y}−\mathrm{6}=\mathrm{0} \\ $$$$−−−−−−− \\ $$$$\mathrm{7}{y}−\mathrm{5}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\frac{\mathrm{5}}{\mathrm{7}}=\mathrm{2}{x}+\mathrm{1}\: \\ $$$${x}=−\frac{\mathrm{1}}{\mathrm{7}}\: \\ $$$${let}\:{x}={X}−\frac{\mathrm{1}}{\mathrm{7}}\:\:\:\:\:\:\:\:\:\:{dx}={dX} \\ $$$$\:\:\:\:\:\:\:\:{y}={Y}+\frac{\mathrm{5}}{\mathrm{7}}\:\:\:\:\:\:\:\:\:\:{dy}={dY} \\ $$$$\frac{{dY}}{{dX}}=\frac{\mathrm{2}\left({X}−\frac{\mathrm{1}}{\mathrm{7}}\right)−\left({Y}+\frac{\mathrm{5}}{\mathrm{7}}\right)+\mathrm{1}}{\left({X}−\frac{\mathrm{1}}{\mathrm{7}}\right)−\mathrm{4}\left({Y}+\frac{\mathrm{5}}{\mathrm{7}}\right)+\mathrm{3}} \\ $$$$\frac{{dY}}{{dX}}=\frac{\mathrm{2}{X}−{Y}}{{X}−\mathrm{4}{Y}} \\ $$$$\frac{{dY}}{{dX}}=\frac{\mathrm{2}−\frac{{Y}}{{X}}}{\mathrm{1}−\mathrm{4}\frac{{Y}}{{x}}} \\ $$$${let}\:\frac{{Y}}{{X}}={v} \\ $$$$ \\ $$$$\frac{{dY}}{{dX}}={v}+{X}\frac{{dv}}{{dX}} \\ $$$${v}+{X}\frac{{dv}}{{dX}}=\frac{\mathrm{2}−{v}}{\mathrm{1}−\mathrm{4}{v}} \\ $$$${X}\frac{{dv}}{{dX}}=\frac{\mathrm{2}−{v}}{\mathrm{1}−\mathrm{4}{v}}−{v} \\ $$$${X}\frac{{dv}}{{dX}}=\frac{\mathrm{2}−{v}−\left(\mathrm{1}−\mathrm{4}{v}\right)\left({v}\right)}{\mathrm{1}−\mathrm{4}{v}} \\ $$$${X}\frac{{dv}}{{dX}}=\frac{\mathrm{2}−{v}−{v}+\mathrm{4}{v}^{\mathrm{2}} }{\mathrm{1}−\mathrm{4}{v}} \\ $$$$\frac{\mathrm{1}−\mathrm{4}{v}}{\mathrm{4}{v}^{\mathrm{2}} −\mathrm{2}{v}+\mathrm{2}}{dv}=\frac{{dx}}{{X}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{4}{v}−\mathrm{1}}{\mathrm{2}{v}^{\mathrm{2}} −{v}+\mathrm{2}}{dv}=\int\frac{{dx}}{{X}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}{v}^{\mathrm{2}} −{v}+\mathrm{2}\right)={ln}\left({X}\right)+{c} \\ $$$${ln}\left(\mathrm{2}{v}^{\mathrm{2}} −{v}+\mathrm{2}\right)=−{ln}\left({X}\right)+{C}_{\mathrm{1}} \\ $$$$\mathrm{2}{v}^{\mathrm{2}} −{v}+\mathrm{2}=\frac{{C}_{\mathrm{2}} }{{X}} \\ $$$$\mathrm{2}\left(\frac{{Y}}{{X}}\right)^{\mathrm{2}} −\frac{{Y}}{{x}}+\mathrm{2}=\frac{{C}_{\mathrm{2}} }{{X}} \\ $$$$\left({x}+\frac{\mathrm{1}}{\mathrm{7}}\right)\left(\mathrm{2}\left(\frac{{y}−\frac{\mathrm{5}}{\mathrm{7}}}{{x}+\frac{\mathrm{1}}{\mathrm{7}}}\right)^{\mathrm{2}} −\frac{{y}−\frac{\mathrm{5}}{\mathrm{7}}}{{x}+\frac{\mathrm{1}}{\mathrm{7}}}+\mathrm{2}\right)={C}_{\mathrm{2}} \\ $$$$ \\ $$

Commented by Tawa11 last updated on 03/May/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 03/May/22

let x=u+a, y=v+b 2x−y+1=2u−v+(2a−b+1) x−4y+3=u−3b+(a−4b+3) set 2a−b+1=0 a−4b+3=0 i.e. a=−(1/7), b=(5/7) ⇒(dy/dx)=((2u−v)/(u−4v)) ⇒(dv/du)=((2u−v)/(u−4v)) let v=ut (dv/du)=t+u(dt/du) ⇒t+u(dt/du)=((2−t)/(1−4t)) ⇒u(dt/du)=((2(1−t+2t^2 ))/(1−4t)) ⇒(((4t−1)dt)/(2t^2 −t+1))=−((2du)/u) ⇒∫(((4t−1)dt)/(2t^2 −t+1))=−∫((2du)/u) ⇒∫((d(2t^2 −t+1))/(2t^2 −t+1))=−∫((2du)/u) ⇒ln (2t^2 −t+1)=−2ln u+C (2t^2 −t+1)u^2 =C (((2v^2 )/u^2 )−(v/u)+1)u^2 =C [2(((y+(5/7))/(x−(1/7))))^2 −(((y+(5/7))/(x−(1/7))))+1](x−(1/7))^2 =C ⇒[2(((7y+5)/(7x−1)))^2 −((7y+5)/(7x−1))+1](7x−1)^2 =C

$${let}\:{x}={u}+{a},\:{y}={v}+{b} \\ $$$$\mathrm{2}{x}−{y}+\mathrm{1}=\mathrm{2}{u}−{v}+\left(\mathrm{2}{a}−{b}+\mathrm{1}\right) \\ $$$${x}−\mathrm{4}{y}+\mathrm{3}={u}−\mathrm{3}{b}+\left({a}−\mathrm{4}{b}+\mathrm{3}\right) \\ $$$${set} \\ $$$$\mathrm{2}{a}−{b}+\mathrm{1}=\mathrm{0} \\ $$$${a}−\mathrm{4}{b}+\mathrm{3}=\mathrm{0} \\ $$$${i}.{e}.\:{a}=−\frac{\mathrm{1}}{\mathrm{7}},\:{b}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{2}{u}−{v}}{{u}−\mathrm{4}{v}} \\ $$$$\Rightarrow\frac{{dv}}{{du}}=\frac{\mathrm{2}{u}−{v}}{{u}−\mathrm{4}{v}} \\ $$$${let}\:{v}={ut} \\ $$$$\frac{{dv}}{{du}}={t}+{u}\frac{{dt}}{{du}} \\ $$$$\Rightarrow{t}+{u}\frac{{dt}}{{du}}=\frac{\mathrm{2}−{t}}{\mathrm{1}−\mathrm{4}{t}} \\ $$$$\Rightarrow{u}\frac{{dt}}{{du}}=\frac{\mathrm{2}\left(\mathrm{1}−{t}+\mathrm{2}{t}^{\mathrm{2}} \right)}{\mathrm{1}−\mathrm{4}{t}} \\ $$$$\Rightarrow\frac{\left(\mathrm{4}{t}−\mathrm{1}\right){dt}}{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}=−\frac{\mathrm{2}{du}}{{u}} \\ $$$$\Rightarrow\int\frac{\left(\mathrm{4}{t}−\mathrm{1}\right){dt}}{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}=−\int\frac{\mathrm{2}{du}}{{u}} \\ $$$$\Rightarrow\int\frac{{d}\left(\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}\right)}{\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}}=−\int\frac{\mathrm{2}{du}}{{u}} \\ $$$$\Rightarrow\mathrm{ln}\:\left(\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}\right)=−\mathrm{2ln}\:{u}+{C} \\ $$$$\left(\mathrm{2}{t}^{\mathrm{2}} −{t}+\mathrm{1}\right){u}^{\mathrm{2}} ={C} \\ $$$$\left(\frac{\mathrm{2}{v}^{\mathrm{2}} }{{u}^{\mathrm{2}} }−\frac{{v}}{{u}}+\mathrm{1}\right){u}^{\mathrm{2}} ={C} \\ $$$$\left[\mathrm{2}\left(\frac{{y}+\frac{\mathrm{5}}{\mathrm{7}}}{{x}−\frac{\mathrm{1}}{\mathrm{7}}}\right)^{\mathrm{2}} −\left(\frac{{y}+\frac{\mathrm{5}}{\mathrm{7}}}{{x}−\frac{\mathrm{1}}{\mathrm{7}}}\right)+\mathrm{1}\right]\left({x}−\frac{\mathrm{1}}{\mathrm{7}}\right)^{\mathrm{2}} ={C} \\ $$$$\Rightarrow\left[\mathrm{2}\left(\frac{\mathrm{7}{y}+\mathrm{5}}{\mathrm{7}{x}−\mathrm{1}}\right)^{\mathrm{2}} −\frac{\mathrm{7}{y}+\mathrm{5}}{\mathrm{7}{x}−\mathrm{1}}+\mathrm{1}\right]\left(\mathrm{7}{x}−\mathrm{1}\right)^{\mathrm{2}} ={C} \\ $$

Commented by Tawa11 last updated on 03/May/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by princeDera last updated on 15/Aug/22

(dy/dx) = ((2x−y+1)/(x−4y+3)) (x−4y+3)dy + (y−2x−1)dx = 0 m = x−4y+3 and n=y−2x−1 (∂/∂x)m = 1 and (∂/∂y)n = 1 the D.E is exact the solution is of the form f(x,y) = c (∂/∂x)f(x,y) = y − 2x − 1 f(x,y) = ∫(y−2x−1)dx = xy − x^2 − x + h(y) (∂/∂y)f(x,y) = x + h′(y) = x − 4y + 3 h′(y) = 3−4y h(y) = 3y − 2y^2 the solution to the D.E = f(x,y) = c xy−x^2 −x+3y−2y^2 = c

$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}\:=\:\frac{\mathrm{2}\boldsymbol{{x}}−\boldsymbol{{y}}+\mathrm{1}}{\boldsymbol{{x}}−\mathrm{4}\boldsymbol{{y}}+\mathrm{3}} \\ $$$$ \\ $$$$\left(\boldsymbol{{x}}−\mathrm{4}\boldsymbol{{y}}+\mathrm{3}\right)\boldsymbol{{dy}}\:+\:\left(\boldsymbol{{y}}−\mathrm{2}\boldsymbol{{x}}−\mathrm{1}\right)\boldsymbol{{dx}}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\boldsymbol{{m}}\:=\:\boldsymbol{{x}}−\mathrm{4}\boldsymbol{{y}}+\mathrm{3}\:\boldsymbol{{and}}\:\boldsymbol{{n}}=\boldsymbol{{y}}−\mathrm{2}\boldsymbol{{x}}−\mathrm{1} \\ $$$$\frac{\partial}{\partial\boldsymbol{{x}}}\boldsymbol{{m}}\:=\:\mathrm{1}\:\boldsymbol{{and}}\:\frac{\partial}{\partial\boldsymbol{{y}}}\boldsymbol{{n}}\:=\:\mathrm{1} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{D}}.\boldsymbol{{E}}\:\boldsymbol{{is}}\:\boldsymbol{{exact}} \\ $$$$ \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{solution}}\:\boldsymbol{{is}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{form}}\:\boldsymbol{{f}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)\:=\:\boldsymbol{{c}} \\ $$$$\frac{\partial}{\partial\boldsymbol{{x}}}\boldsymbol{{f}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)\:=\:\boldsymbol{{y}}\:−\:\mathrm{2}\boldsymbol{{x}}\:−\:\mathrm{1} \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)\:=\:\int\left(\boldsymbol{{y}}−\mathrm{2}\boldsymbol{{x}}−\mathrm{1}\right)\boldsymbol{{dx}}\:=\:\boldsymbol{{xy}}\:−\:\boldsymbol{{x}}^{\mathrm{2}} \:−\:\boldsymbol{{x}}\:+\:\boldsymbol{{h}}\left(\boldsymbol{{y}}\right) \\ $$$$ \\ $$$$\frac{\partial}{\partial\boldsymbol{{y}}}\boldsymbol{{f}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)\:=\:\boldsymbol{{x}}\:+\:\boldsymbol{{h}}'\left(\boldsymbol{{y}}\right)\:=\:\boldsymbol{{x}}\:−\:\mathrm{4}\boldsymbol{{y}}\:+\:\mathrm{3} \\ $$$$\boldsymbol{{h}}'\left(\boldsymbol{{y}}\right)\:=\:\mathrm{3}−\mathrm{4}\boldsymbol{{y}} \\ $$$$\boldsymbol{{h}}\left(\boldsymbol{{y}}\right)\:=\:\mathrm{3}\boldsymbol{{y}}\:−\:\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{solution}}\:\boldsymbol{{to}}\:\boldsymbol{{the}}\:\boldsymbol{{D}}.\boldsymbol{{E}}\:=\:\boldsymbol{{f}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)\:=\:\boldsymbol{{c}} \\ $$$$\boldsymbol{{xy}}−\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{x}}+\mathrm{3}\boldsymbol{{y}}−\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} \:=\:\boldsymbol{{c}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com