Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 169585 by Shrinava last updated on 03/May/22

Commented by mr W last updated on 03/May/22

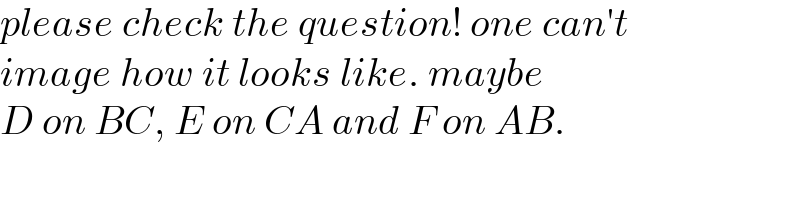
please check the question! one can′t image how it looks like. maybe D on BC, E on CA and F on AB.

$${please}\:{check}\:{the}\:{question}!\:{one}\:{can}'{t} \\ $$$${image}\:{how}\:{it}\:{looks}\:{like}.\:{maybe} \\ $$$${D}\:{on}\:{BC},\:{E}\:{on}\:{CA}\:{and}\:{F}\:{on}\:{AB}. \\ $$

Commented by Shrinava last updated on 03/May/22

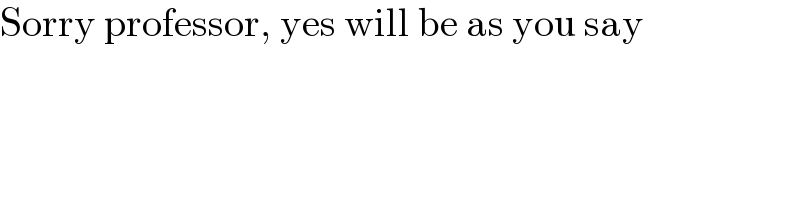
Sorry professor, yes will be as you say

$$\mathrm{Sorry}\:\mathrm{professor},\:\mathrm{yes}\:\mathrm{will}\:\mathrm{be}\:\mathrm{as}\:\mathrm{you}\:\mathrm{say} \\ $$

Answered by mr W last updated on 03/May/22

Commented by mr W last updated on 03/May/22

it′s easy to see that ΔEFD∼ΔABC ⇒(p/c)=(q/a)=(r/b)=k, say ⇒p=kc, q=ka, r=kb a=(q/(tan B))+(r/(sin C)) ⇒a((1/k)−(1/(tan B)))=(b/(sin C)) ...(i) b=(r/(tan C))+(p/(sin A)) ⇒b((1/k)−(1/(tan C)))=(c/(sin A)) ...(ii) c=(p/(tan A))+(q/(sin B)) ⇒c((1/k)−(1/(tan A)))=(a/(sin B)) ...(iii) (i)×(ii)×(iii): ((1/k)−(1/(tan A)))((1/k)−(1/(tan B)))((1/k)−(1/(tan C)))=(1/(sin A sin B sin C)) ((1/k)−((cos A)/(sin A)))((1/k)−((cos B)/(sin B)))((1/k)−((cos C)/(sin C)))=(1/(sin A sin B sin C)) (sin A−k cos A)(sin B−k cos B)(sin C−k cos C)=k^3 (1+cos A cos B cos C)k^3 −(sin A sin B sin C)k^2 +(1+cos A cos B cos C)k−sin A sin B sin C=0 (k−((sin A sin B sin C)/(1+cos A cos B cos C)))(k^2 +1)=0 ⇒k=((sin A sin B sin C)/(1+cos A cos B cos C)) (p/a)+(q/b)+(r/c)=k((c/a)+(a/b)+(b/c)) ≥3k maximum if (c/a)=(a/b)=(b/c), i.e. a=b=c, i.e. A=B=C=(π/3) and k=((sin A sin B sin C)/(1+cos A cos B cos C))=(((((√3)/2))^3 )/(1+((1/2))^3 ))=((√3)/3) ⇒(p/a)+(q/b)+(r/c)≥3k=3×((√3)/3)=(√3) ✓

$${it}'{s}\:{easy}\:{to}\:{see}\:{that} \\ $$$$\Delta{EFD}\sim\Delta{ABC} \\ $$$$\Rightarrow\frac{{p}}{{c}}=\frac{{q}}{{a}}=\frac{{r}}{{b}}={k},\:{say} \\ $$$$\Rightarrow{p}={kc},\:{q}={ka},\:{r}={kb} \\ $$$$ \\ $$$${a}=\frac{{q}}{\mathrm{tan}\:{B}}+\frac{{r}}{\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{a}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{\mathrm{tan}\:{B}}\right)=\frac{{b}}{\mathrm{sin}\:{C}}\:\:\:...\left({i}\right) \\ $$$${b}=\frac{{r}}{\mathrm{tan}\:{C}}+\frac{{p}}{\mathrm{sin}\:{A}} \\ $$$$\Rightarrow{b}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{\mathrm{tan}\:{C}}\right)=\frac{{c}}{\mathrm{sin}\:{A}}\:\:\:...\left({ii}\right) \\ $$$${c}=\frac{{p}}{\mathrm{tan}\:{A}}+\frac{{q}}{\mathrm{sin}\:{B}} \\ $$$$\Rightarrow{c}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{\mathrm{tan}\:{A}}\right)=\frac{{a}}{\mathrm{sin}\:{B}}\:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)×\left({ii}\right)×\left({iii}\right): \\ $$$$\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{\mathrm{tan}\:{A}}\right)\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{\mathrm{tan}\:{B}}\right)\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{\mathrm{tan}\:{C}}\right)=\frac{\mathrm{1}}{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{cos}\:{A}}{\mathrm{sin}\:{A}}\right)\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{cos}\:{B}}{\mathrm{sin}\:{B}}\right)\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{cos}\:{C}}{\mathrm{sin}\:{C}}\right)=\frac{\mathrm{1}}{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\left(\mathrm{sin}\:{A}−{k}\:\mathrm{cos}\:{A}\right)\left(\mathrm{sin}\:{B}−{k}\:\mathrm{cos}\:{B}\right)\left(\mathrm{sin}\:{C}−{k}\:\mathrm{cos}\:{C}\right)={k}^{\mathrm{3}} \\ $$$$\left(\mathrm{1}+\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right){k}^{\mathrm{3}} −\left(\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\right){k}^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\right){k}−\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}=\mathrm{0} \\ $$$$\left({k}−\frac{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}{\mathrm{1}+\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}}\right)\left({k}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}{\mathrm{1}+\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}} \\ $$$$ \\ $$$$\frac{{p}}{{a}}+\frac{{q}}{{b}}+\frac{{r}}{{c}}={k}\left(\frac{{c}}{{a}}+\frac{{a}}{{b}}+\frac{{b}}{{c}}\right)\:\geqslant\mathrm{3}{k} \\ $$$${maximum}\:{if}\:\frac{{c}}{{a}}=\frac{{a}}{{b}}=\frac{{b}}{{c}},\:{i}.{e}.\:{a}={b}={c}, \\ $$$${i}.{e}.\:{A}={B}={C}=\frac{\pi}{\mathrm{3}}\:{and} \\ $$$${k}=\frac{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}{\mathrm{1}+\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}}=\frac{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{3}} }{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{p}}{{a}}+\frac{{q}}{{b}}+\frac{{r}}{{c}}\geqslant\mathrm{3}{k}=\mathrm{3}×\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}=\sqrt{\mathrm{3}}\:\checkmark \\ $$

Commented by Shrinava last updated on 04/May/22

As always, the perfect solution, thank you so much Professor

$$\mathrm{As}\:\mathrm{always},\:\mathrm{the}\:\mathrm{perfect}\:\mathrm{solution}, \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\:\mathrm{Professor} \\ $$

Commented by Tawa11 last updated on 04/May/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com