Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 169600 by bounhome last updated on 04/May/22

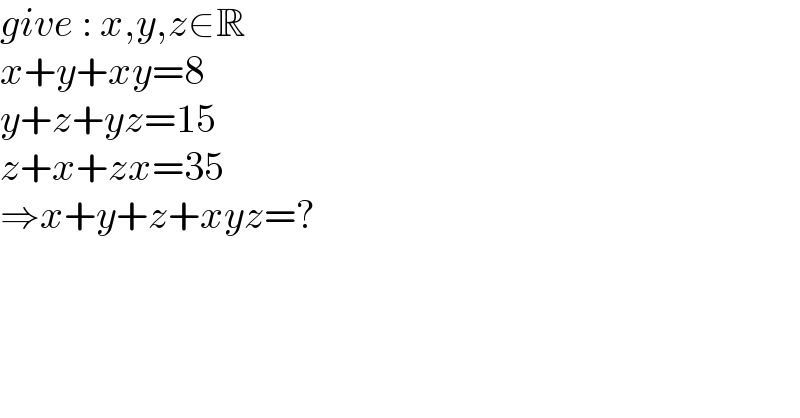
give : x,y,z∈R x+y+xy=8 y+z+yz=15 z+x+zx=35 ⇒x+y+z+xyz=?

$${give}\::\:{x},{y},{z}\in\mathbb{R}\: \\ $$$${x}+{y}+{xy}=\mathrm{8} \\ $$$${y}+{z}+{yz}=\mathrm{15} \\ $$$${z}+{x}+{zx}=\mathrm{35} \\ $$$$\Rightarrow{x}+{y}+{z}+{xyz}=? \\ $$

Commented by infinityaction last updated on 04/May/22

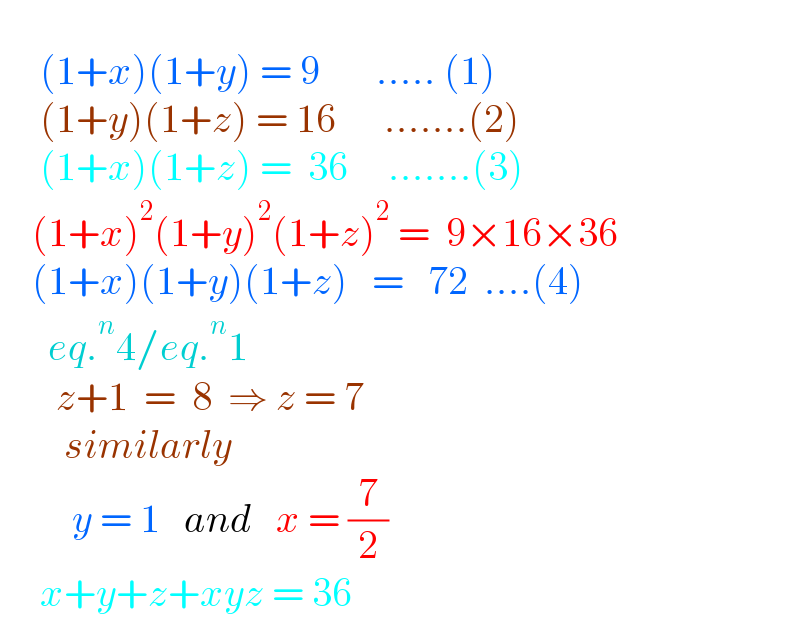
(1+x)(1+y) = 9 ..... (1) (1+y)(1+z) = 16 .......(2) (1+x)(1+z) = 36 .......(3) (1+x)^2 (1+y)^2 (1+z)^2 = 9×16×36 (1+x)(1+y)(1+z) = 72 ....(4) eq.^n 4/eq.^n 1 z+1 = 8 ⇒ z = 7 similarly y = 1 and x = (7/2) x+y+z+xyz = 36

$$ \\ $$$$\:\:\:\:\:\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{y}\right)\:=\:\mathrm{9}\:\:\:\:\:\:\:.....\:\left(\mathrm{1}\right) \\ $$$$\:\:\:\:\:\left(\mathrm{1}+{y}\right)\left(\mathrm{1}+{z}\right)\:=\:\mathrm{16}\:\:\:\:\:\:.......\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{z}\right)\:=\:\:\mathrm{36}\:\:\:\:\:.......\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \left(\mathrm{1}+{y}\right)^{\mathrm{2}} \left(\mathrm{1}+{z}\right)^{\mathrm{2}} \:=\:\:\mathrm{9}×\mathrm{16}×\mathrm{36} \\ $$$$\:\:\:\:\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{y}\right)\left(\mathrm{1}+{z}\right)\:\:\:=\:\:\:\mathrm{72}\:\:....\left(\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:{eq}.^{{n}} \mathrm{4}/{eq}.^{{n}} \mathrm{1} \\ $$$$\:\:\:\:\:\:\:{z}+\mathrm{1}\:\:=\:\:\mathrm{8}\:\:\Rightarrow\:{z}\:=\:\mathrm{7} \\ $$$$\:\:\:\:\:\:\:\:{similarly} \\ $$$$\:\:\:\:\:\:\:\:\:{y}\:=\:\mathrm{1}\:\:\:{and}\:\:\:{x}\:=\:\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\:\:\:\:\:{x}+{y}+{z}+{xyz}\:=\:\mathrm{36} \\ $$

Commented by Tawa11 last updated on 04/May/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 04/May/22

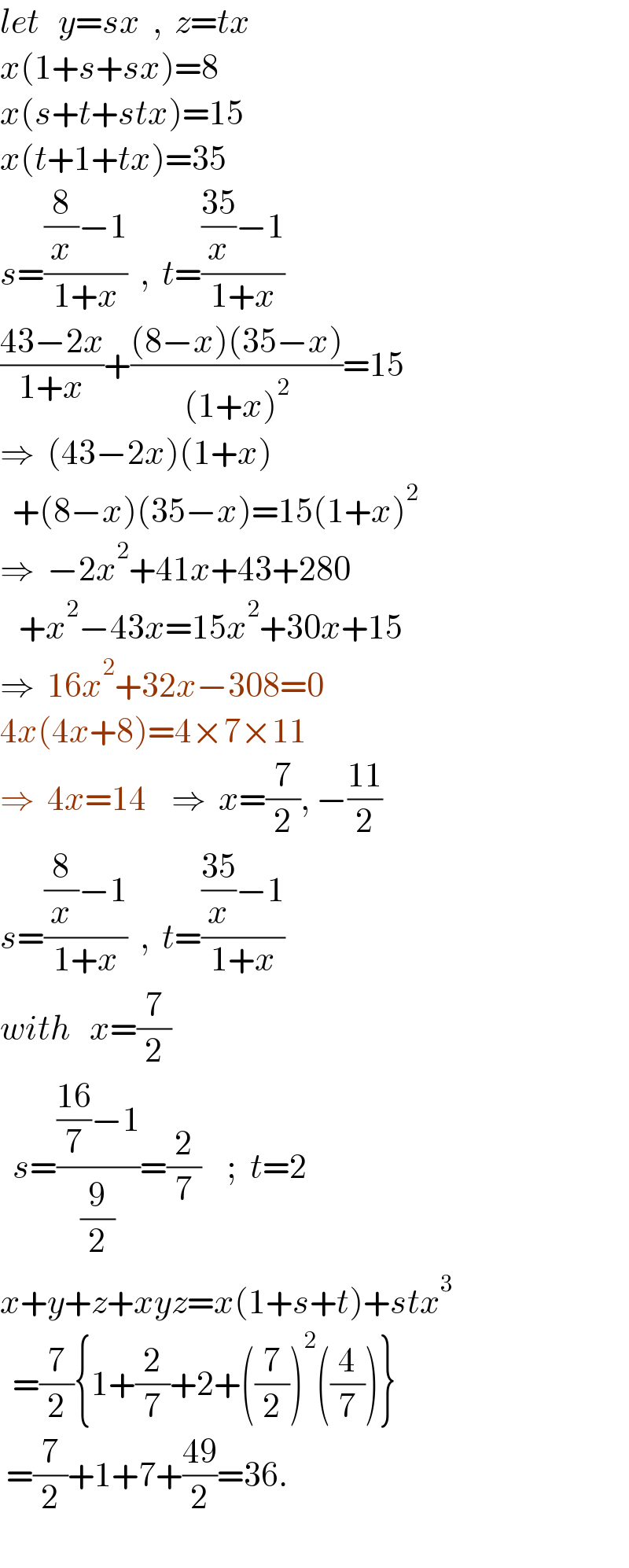
let y=sx , z=tx x(1+s+sx)=8 x(s+t+stx)=15 x(t+1+tx)=35 s=(((8/x)−1)/(1+x)) , t=((((35)/x)−1)/(1+x)) ((43−2x)/(1+x))+(((8−x)(35−x))/((1+x)^2 ))=15 ⇒ (43−2x)(1+x) +(8−x)(35−x)=15(1+x)^2 ⇒ −2x^2 +41x+43+280 +x^2 −43x=15x^2 +30x+15 ⇒ 16x^2 +32x−308=0 4x(4x+8)=4×7×11 ⇒ 4x=14 ⇒ x=(7/2), −((11)/2) s=(((8/x)−1)/(1+x)) , t=((((35)/x)−1)/(1+x)) with x=(7/2) s=((((16)/7)−1)/(9/2))=(2/7) ; t=2 x+y+z+xyz=x(1+s+t)+stx^3 =(7/2){1+(2/7)+2+((7/2))^2 ((4/7))} =(7/2)+1+7+((49)/2)=36.

$${let}\:\:\:{y}={sx}\:\:,\:\:{z}={tx} \\ $$$${x}\left(\mathrm{1}+{s}+{sx}\right)=\mathrm{8} \\ $$$${x}\left({s}+{t}+{stx}\right)=\mathrm{15} \\ $$$${x}\left({t}+\mathrm{1}+{tx}\right)=\mathrm{35} \\ $$$${s}=\frac{\frac{\mathrm{8}}{{x}}−\mathrm{1}}{\mathrm{1}+{x}}\:\:,\:\:{t}=\frac{\frac{\mathrm{35}}{{x}}−\mathrm{1}}{\mathrm{1}+{x}} \\ $$$$\frac{\mathrm{43}−\mathrm{2}{x}}{\mathrm{1}+{x}}+\frac{\left(\mathrm{8}−{x}\right)\left(\mathrm{35}−{x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\mathrm{15} \\ $$$$\Rightarrow\:\:\left(\mathrm{43}−\mathrm{2}{x}\right)\left(\mathrm{1}+{x}\right) \\ $$$$\:\:+\left(\mathrm{8}−{x}\right)\left(\mathrm{35}−{x}\right)=\mathrm{15}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{41}{x}+\mathrm{43}+\mathrm{280} \\ $$$$\:\:\:+{x}^{\mathrm{2}} −\mathrm{43}{x}=\mathrm{15}{x}^{\mathrm{2}} +\mathrm{30}{x}+\mathrm{15} \\ $$$$\Rightarrow\:\:\mathrm{16}{x}^{\mathrm{2}} +\mathrm{32}{x}−\mathrm{308}=\mathrm{0} \\ $$$$\mathrm{4}{x}\left(\mathrm{4}{x}+\mathrm{8}\right)=\mathrm{4}×\mathrm{7}×\mathrm{11} \\ $$$$\Rightarrow\:\:\mathrm{4}{x}=\mathrm{14}\:\:\:\:\Rightarrow\:\:{x}=\frac{\mathrm{7}}{\mathrm{2}},\:−\frac{\mathrm{11}}{\mathrm{2}} \\ $$$${s}=\frac{\frac{\mathrm{8}}{{x}}−\mathrm{1}}{\mathrm{1}+{x}}\:\:,\:\:{t}=\frac{\frac{\mathrm{35}}{{x}}−\mathrm{1}}{\mathrm{1}+{x}} \\ $$$${with}\:\:\:{x}=\frac{\mathrm{7}}{\mathrm{2}} \\ $$$$\:\:{s}=\frac{\frac{\mathrm{16}}{\mathrm{7}}−\mathrm{1}}{\frac{\mathrm{9}}{\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{7}}\:\:\:\:;\:\:{t}=\mathrm{2} \\ $$$${x}+{y}+{z}+{xyz}={x}\left(\mathrm{1}+{s}+{t}\right)+{stx}^{\mathrm{3}} \\ $$$$\:\:=\frac{\mathrm{7}}{\mathrm{2}}\left\{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{7}}+\mathrm{2}+\left(\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\frac{\mathrm{4}}{\mathrm{7}}\right)\right\} \\ $$$$\:=\frac{\mathrm{7}}{\mathrm{2}}+\mathrm{1}+\mathrm{7}+\frac{\mathrm{49}}{\mathrm{2}}=\mathrm{36}. \\ $$$$ \\ $$

Commented by Tawa11 last updated on 04/May/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 04/May/22

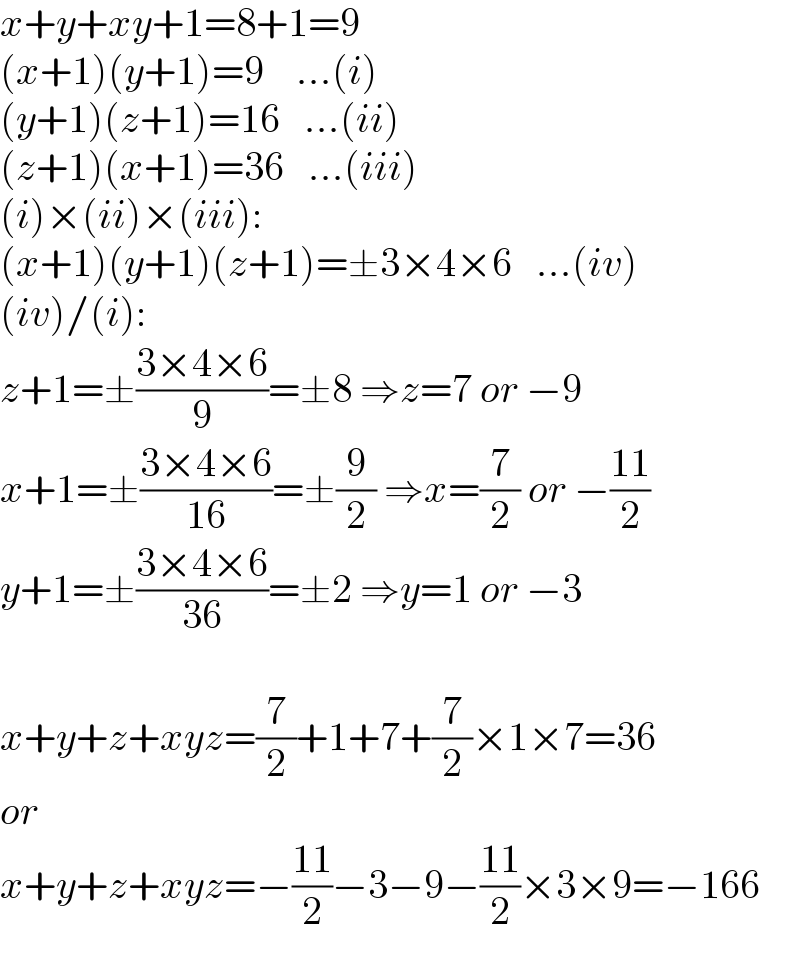
x+y+xy+1=8+1=9 (x+1)(y+1)=9 ...(i) (y+1)(z+1)=16 ...(ii) (z+1)(x+1)=36 ...(iii) (i)×(ii)×(iii): (x+1)(y+1)(z+1)=±3×4×6 ...(iv) (iv)/(i): z+1=±((3×4×6)/9)=±8 ⇒z=7 or −9 x+1=±((3×4×6)/(16))=±(9/2) ⇒x=(7/2) or −((11)/2) y+1=±((3×4×6)/(36))=±2 ⇒y=1 or −3 x+y+z+xyz=(7/2)+1+7+(7/2)×1×7=36 or x+y+z+xyz=−((11)/2)−3−9−((11)/2)×3×9=−166

$${x}+{y}+{xy}+\mathrm{1}=\mathrm{8}+\mathrm{1}=\mathrm{9} \\ $$$$\left({x}+\mathrm{1}\right)\left({y}+\mathrm{1}\right)=\mathrm{9}\:\:\:\:...\left({i}\right) \\ $$$$\left({y}+\mathrm{1}\right)\left({z}+\mathrm{1}\right)=\mathrm{16}\:\:\:...\left({ii}\right) \\ $$$$\left({z}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)=\mathrm{36}\:\:\:...\left({iii}\right) \\ $$$$\left({i}\right)×\left({ii}\right)×\left({iii}\right): \\ $$$$\left({x}+\mathrm{1}\right)\left({y}+\mathrm{1}\right)\left({z}+\mathrm{1}\right)=\pm\mathrm{3}×\mathrm{4}×\mathrm{6}\:\:\:...\left({iv}\right) \\ $$$$\left({iv}\right)/\left({i}\right): \\ $$$${z}+\mathrm{1}=\pm\frac{\mathrm{3}×\mathrm{4}×\mathrm{6}}{\mathrm{9}}=\pm\mathrm{8}\:\Rightarrow{z}=\mathrm{7}\:{or}\:−\mathrm{9} \\ $$$${x}+\mathrm{1}=\pm\frac{\mathrm{3}×\mathrm{4}×\mathrm{6}}{\mathrm{16}}=\pm\frac{\mathrm{9}}{\mathrm{2}}\:\Rightarrow{x}=\frac{\mathrm{7}}{\mathrm{2}}\:{or}\:−\frac{\mathrm{11}}{\mathrm{2}} \\ $$$${y}+\mathrm{1}=\pm\frac{\mathrm{3}×\mathrm{4}×\mathrm{6}}{\mathrm{36}}=\pm\mathrm{2}\:\Rightarrow{y}=\mathrm{1}\:{or}\:−\mathrm{3} \\ $$$$ \\ $$$${x}+{y}+{z}+{xyz}=\frac{\mathrm{7}}{\mathrm{2}}+\mathrm{1}+\mathrm{7}+\frac{\mathrm{7}}{\mathrm{2}}×\mathrm{1}×\mathrm{7}=\mathrm{36} \\ $$$${or} \\ $$$${x}+{y}+{z}+{xyz}=−\frac{\mathrm{11}}{\mathrm{2}}−\mathrm{3}−\mathrm{9}−\frac{\mathrm{11}}{\mathrm{2}}×\mathrm{3}×\mathrm{9}=−\mathrm{166} \\ $$

Commented by Tawa11 last updated on 04/May/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by ajfour last updated on 06/May/22

z=((35−x)/(1+x))=((15−y)/(1+y)) ⇒ 35+35y−x=15+15x−y ⇒ 36y+20=16x ⇒ 9y+5=4x (9y+5)+4y+y(9y+5)=32 9y^2 +18y−27=0 y^2 +2y+1=4 ⇒ y+1=±2 y= −3, 1 corresponding x= −((11)/2), (7/2) z=((15−y)/(1+y))= −9, 7 x+y+z+xyz= −17−(1/2)−((297)/2) = −166 or = 11+(1/2)+((49)/2)= 36

$${z}=\frac{\mathrm{35}−{x}}{\mathrm{1}+{x}}=\frac{\mathrm{15}−{y}}{\mathrm{1}+{y}} \\ $$$$\Rightarrow\:\:\:\mathrm{35}+\mathrm{35}{y}−{x}=\mathrm{15}+\mathrm{15}{x}−{y} \\ $$$$\Rightarrow\:\:\mathrm{36}{y}+\mathrm{20}=\mathrm{16}{x} \\ $$$$\Rightarrow\:\:\:\mathrm{9}{y}+\mathrm{5}=\mathrm{4}{x} \\ $$$$\left(\mathrm{9}{y}+\mathrm{5}\right)+\mathrm{4}{y}+{y}\left(\mathrm{9}{y}+\mathrm{5}\right)=\mathrm{32} \\ $$$$\mathrm{9}{y}^{\mathrm{2}} +\mathrm{18}{y}−\mathrm{27}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{1}=\mathrm{4} \\ $$$$\Rightarrow\:\:{y}+\mathrm{1}=\pm\mathrm{2} \\ $$$${y}=\:−\mathrm{3},\:\mathrm{1} \\ $$$${corresponding}\:{x}=\:−\frac{\mathrm{11}}{\mathrm{2}},\:\frac{\mathrm{7}}{\mathrm{2}} \\ $$$${z}=\frac{\mathrm{15}−{y}}{\mathrm{1}+{y}}=\:−\mathrm{9},\:\mathrm{7} \\ $$$${x}+{y}+{z}+{xyz}=\:−\mathrm{17}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{297}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\:−\mathrm{166} \\ $$$${or}\:=\:\mathrm{11}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{49}}{\mathrm{2}}=\:\mathrm{36} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com