Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 169655 by Shrinava last updated on 05/May/22

Answered by mr W last updated on 07/May/22

Commented by Shrinava last updated on 07/May/22

Professor, the picture is perfect

$$\mathrm{Professor},\:\mathrm{the}\:\mathrm{picture}\:\mathrm{is}\:\mathrm{perfect} \\ $$

Commented by Shrinava last updated on 07/May/22

Professof, I look forward to your perfect solution, thank you

$$\mathrm{Professof},\:\mathrm{I}\:\mathrm{look}\:\mathrm{forward}\:\mathrm{to}\:\mathrm{your}\:\mathrm{perfect} \\ $$$$\mathrm{solution},\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by mr W last updated on 08/May/22

i didn′t get the same result as in the question.

$${i}\:{didn}'{t}\:{get}\:{the}\:{same}\:{result}\:{as}\:{in}\:{the} \\ $$$${question}. \\ $$

Commented by Shrinava last updated on 08/May/22

Is interesting, thank you so much Professor

$$\mathrm{Is}\:\mathrm{interesting},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{Professor} \\ $$

Commented by mr W last updated on 09/May/22

[I_a I_b I_c ]=8R^2 cos (A/2) cos (B/2) cos (C/2) [ABC]=2R^2 sin A sin B sin C [ABC]=16R^2 sin (A/2) sin (B/2) sin (C/2) cos (A/2) cos (B/2) cos (C/2) [I_a I_b I_c ]−[ABC]=8R^2 cos (A/2) cos (B/2) cos (C/2)(1−2 sin (A/2) sin (B/2) sin (C/2)) AE=AF=s−a=((−a+b+c)/2) r_1 =(((s−a)cos (A/2))/(1+(1/(sin (A/2)))))=(((s−a)sin (A/2) cos (A/2))/(1+sin (A/2))) r_1 =((R(−sin A+sin B+sin C) sin (A/2) cos (A/2))/(1+sin (A/2))) r_1 =((4R cos (A/2) sin (B/2) sin (C/2) sin (A/2) cos (A/2))/(1+sin (A/2))) r_1 =((4R sin (A/2) sin (B/2) sin (C/2) cos^2 (A/2))/(1+sin (A/2))) r_1 =4R sin (A/2) sin (B/2) sin (C/2) (1−sin (A/2)) r_1 +r_2 +r_3 =4R sin (A/2) sin (B/2) sin (C/2) (3−sin (A/2)−sin (B/2)−sin (C/2)) this doesn′t prove r_1 +r_2 +r_3 =(([I_a I_b I_c ]−[ABC])/(2R(cos (A/2)+cos (B/2)+cos (C/2))))

$$\left[{I}_{{a}} {I}_{{b}} {I}_{{c}} \right]=\mathrm{8}{R}^{\mathrm{2}} \mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}} \\ $$$$ \\ $$$$\left[{ABC}\right]=\mathrm{2}{R}^{\mathrm{2}} \mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C} \\ $$$$\left[{ABC}\right]=\mathrm{16}{R}^{\mathrm{2}} \:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}} \\ $$$$ \\ $$$$\left[{I}_{{a}} {I}_{{b}} {I}_{{c}} \right]−\left[{ABC}\right]=\mathrm{8}{R}^{\mathrm{2}} \mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\right) \\ $$$$ \\ $$$${AE}={AF}={s}−{a}=\frac{−{a}+{b}+{c}}{\mathrm{2}} \\ $$$${r}_{\mathrm{1}} =\frac{\left({s}−{a}\right)\mathrm{cos}\:\frac{{A}}{\mathrm{2}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{sin}\:\frac{{A}}{\mathrm{2}}}}=\frac{\left({s}−{a}\right)\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}}{\mathrm{1}+\mathrm{sin}\:\frac{{A}}{\mathrm{2}}} \\ $$$${r}_{\mathrm{1}} =\frac{{R}\left(−\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}\right)\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}}{\mathrm{1}+\mathrm{sin}\:\frac{{A}}{\mathrm{2}}} \\ $$$${r}_{\mathrm{1}} =\frac{\mathrm{4}{R}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}}{\mathrm{1}+\mathrm{sin}\:\frac{{A}}{\mathrm{2}}} \\ $$$${r}_{\mathrm{1}} =\frac{\mathrm{4}{R}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\:\mathrm{cos}^{\mathrm{2}} \:\frac{{A}}{\mathrm{2}}}{\mathrm{1}+\mathrm{sin}\:\frac{{A}}{\mathrm{2}}} \\ $$$${r}_{\mathrm{1}} =\mathrm{4}{R}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\:\left(\mathrm{1}−\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\right) \\ $$$${r}_{\mathrm{1}} +{r}_{\mathrm{2}} +{r}_{\mathrm{3}} =\mathrm{4}{R}\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\:\left(\mathrm{3}−\mathrm{sin}\:\frac{{A}}{\mathrm{2}}−\mathrm{sin}\:\frac{{B}}{\mathrm{2}}−\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\right) \\ $$$${this}\:{doesn}'{t}\:{prove} \\ $$$${r}_{\mathrm{1}} +{r}_{\mathrm{2}} +{r}_{\mathrm{3}} =\frac{\left[{I}_{{a}} {I}_{{b}} {I}_{{c}} \right]−\left[{ABC}\right]}{\mathrm{2}{R}\left(\mathrm{cos}\:\frac{{A}}{\mathrm{2}}+\mathrm{cos}\:\frac{{B}}{\mathrm{2}}+\mathrm{cos}\:\frac{{C}}{\mathrm{2}}\right)} \\ $$

Commented by mr W last updated on 09/May/22

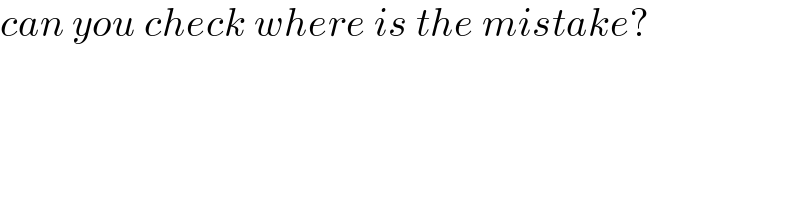
can you check where is the mistake?

$${can}\:{you}\:{check}\:{where}\:{is}\:{the}\:{mistake}? \\ $$

Commented by Shrinava last updated on 09/May/22

Dear Professor, l could not find exactly, but the solution is perfect

$$\mathrm{Dear}\:\mathrm{Professor},\:\mathrm{l}\:\mathrm{could}\:\mathrm{not}\:\mathrm{find}\:\mathrm{exactly}, \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{perfect} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com