
Question and Answers Forum
Question Number 169756 by mokys last updated on 07/May/22

Answered by aleks041103 last updated on 07/May/22
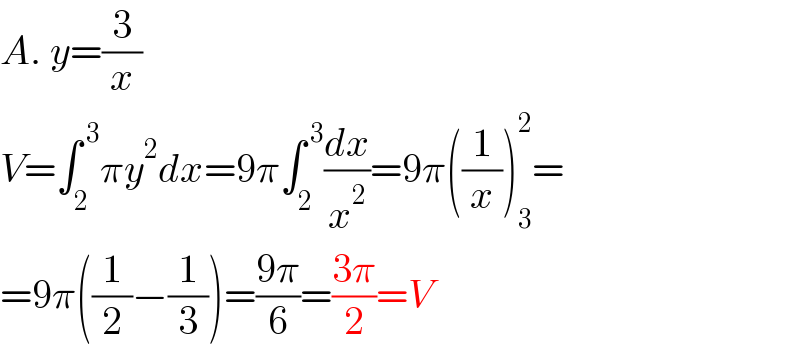
Answered by aleks041103 last updated on 07/May/22
![B. (a) V=∫_0 ^( 3) πy^2 dx=π∫_0 ^( 3) (2x^2 +3)^2 dx= =π∫_0 ^( 3) (4x^4 +12x^2 +9)dx= =π[(4/5)x^5 +4x^3 +9x]_0 ^3 = =π(((4.3^5 )/5)+4.3^3 +9.3)= =π(((36.3^3 )/5)+5.3^3 )= =((27π)/5)(36+25)=((27.61π)/5)](Q169762.png)
Answered by thfchristopher last updated on 08/May/22
![A. For the curve rotates x-axis, y=(3/x) V=π∫_2 ^3 ((3/x))^2 dx =π∫_2 ^3 (9/x^2 )dx =−π[(9/x)]_2 ^3 =((3π)/2) B. (a) For the curve rotates x-axis, V_x =π∫_0 ^3 (2x^2 +3)^2 dx =π∫_0 ^3 (4x^4 +12x^2 +9)dx =π[((4x^5 )/5)+4x^3 +9x]_0 ^3 =((783π)/5) (b) For the curve rotates y-axis, x=(√((y−3)/2)) When x=3, y=21 x=0, y=3 ∴ V_y =π∫_3 ^(21) ((y−3)/2)dy =π[(y^2 /4)−((3y)/2)]_3 ^(21) =81π](Q169796.png)
| ||
Question and Answers Forum | ||
Question Number 169756 by mokys last updated on 07/May/22 | ||
 | ||
Answered by aleks041103 last updated on 07/May/22 | ||
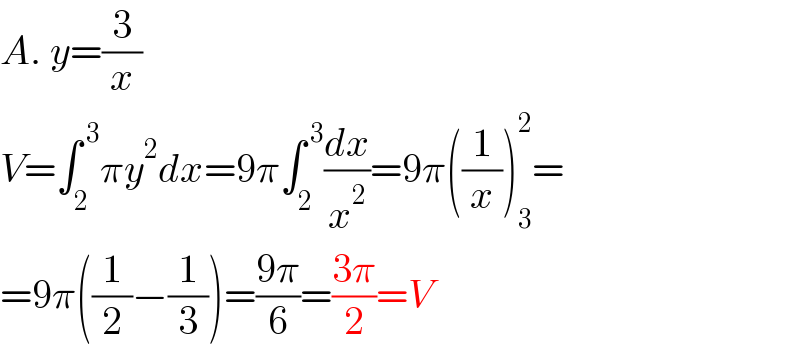 | ||
| ||
Answered by aleks041103 last updated on 07/May/22 | ||
![B. (a) V=∫_0 ^( 3) πy^2 dx=π∫_0 ^( 3) (2x^2 +3)^2 dx= =π∫_0 ^( 3) (4x^4 +12x^2 +9)dx= =π[(4/5)x^5 +4x^3 +9x]_0 ^3 = =π(((4.3^5 )/5)+4.3^3 +9.3)= =π(((36.3^3 )/5)+5.3^3 )= =((27π)/5)(36+25)=((27.61π)/5)](Q169762.png) | ||
| ||
Answered by thfchristopher last updated on 08/May/22 | ||
![A. For the curve rotates x-axis, y=(3/x) V=π∫_2 ^3 ((3/x))^2 dx =π∫_2 ^3 (9/x^2 )dx =−π[(9/x)]_2 ^3 =((3π)/2) B. (a) For the curve rotates x-axis, V_x =π∫_0 ^3 (2x^2 +3)^2 dx =π∫_0 ^3 (4x^4 +12x^2 +9)dx =π[((4x^5 )/5)+4x^3 +9x]_0 ^3 =((783π)/5) (b) For the curve rotates y-axis, x=(√((y−3)/2)) When x=3, y=21 x=0, y=3 ∴ V_y =π∫_3 ^(21) ((y−3)/2)dy =π[(y^2 /4)−((3y)/2)]_3 ^(21) =81π](Q169796.png) | ||
| ||