Question and Answers Forum

All Questions      Topic List

Set Theory Questions

Previous in All Question      Next in All Question      

Previous in Set Theory      Next in Set Theory      

Question Number 1698 by Rasheed Ahmad last updated on 01/Sep/15

•Are A∪B=A∩B and A=B completely equivalent? •Simplify A∪B=A∩B to A=B using set operations and their properties.

$$\bullet{Are}\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}=\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:\:{and}\:\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}}\: \\ $$$${completely}\:{equivalent}? \\ $$$$\bullet{Simplify}\:\boldsymbol{\mathrm{A}}\cup\boldsymbol{\mathrm{B}}=\boldsymbol{\mathrm{A}}\cap\boldsymbol{\mathrm{B}}\:{to}\:\boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{B}} \\ $$$${using}\:{set}\:{operations}\:{and}\:{their} \\ $$$${properties}. \\ $$

Answered by 123456 last updated on 01/Sep/15

if A∪B=A∩B them A=B we have that A∪B=A∩B them ∀x,x∈A∪B,x∈A∩B them supose that A≠B, without loss of generality suppose tbat ∣A∣>∣B∣ x∈A,x∉B x∈A∪B,x∉A∩B (contradition) hence A=B and if A=B, the A∪B=A∪A=A A∩B=A∩A=A A∪B=A∩B so A∪B=A∩B⇔A=B

$$\mathrm{if}\:\mathrm{A}\cup\mathrm{B}=\mathrm{A}\cap\mathrm{B}\:\mathrm{them}\:\mathrm{A}=\mathrm{B} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{that}\:\mathrm{A}\cup\mathrm{B}=\mathrm{A}\cap\mathrm{B}\:\mathrm{them}\:\forall{x},{x}\in\mathrm{A}\cup\mathrm{B},{x}\in\mathrm{A}\cap\mathrm{B} \\ $$$$\mathrm{them}\:\mathrm{supose}\:\mathrm{that}\:\mathrm{A}\neq\mathrm{B},\:\mathrm{without}\:\mathrm{loss} \\ $$$$\mathrm{of}\:\mathrm{generality}\:\mathrm{suppose}\:\mathrm{tbat}\:\mid\mathrm{A}\mid>\mid\mathrm{B}\mid \\ $$$${x}\in\mathrm{A},{x}\notin\mathrm{B} \\ $$$${x}\in\mathrm{A}\cup\mathrm{B},{x}\notin\mathrm{A}\cap\mathrm{B}\:\left(\mathrm{contradition}\right) \\ $$$$\mathrm{hence}\:\mathrm{A}=\mathrm{B} \\ $$$$\mathrm{and}\:\mathrm{if}\:\mathrm{A}=\mathrm{B},\:\mathrm{the} \\ $$$$\mathrm{A}\cup\mathrm{B}=\mathrm{A}\cup\mathrm{A}=\mathrm{A} \\ $$$$\mathrm{A}\cap\mathrm{B}=\mathrm{A}\cap\mathrm{A}=\mathrm{A} \\ $$$$\mathrm{A}\cup\mathrm{B}=\mathrm{A}\cap\mathrm{B} \\ $$$$\mathrm{so} \\ $$$$\mathrm{A}\cup\mathrm{B}=\mathrm{A}\cap\mathrm{B}\Leftrightarrow\mathrm{A}=\mathrm{B} \\ $$

Answered by 123456 last updated on 01/Sep/15

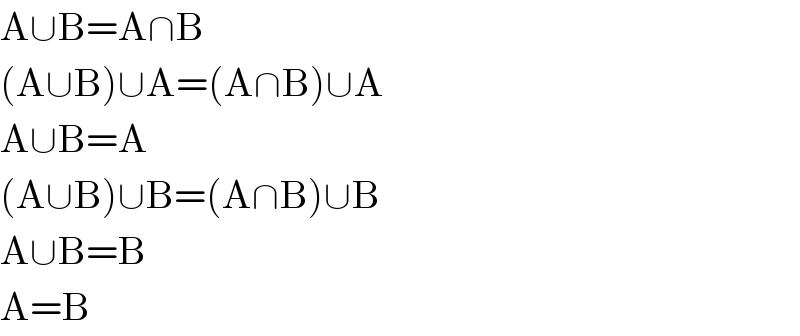
A∪B=A∩B (A∪B)∪A=(A∩B)∪A A∪B=A (A∪B)∪B=(A∩B)∪B A∪B=B A=B

$$\mathrm{A}\cup\mathrm{B}=\mathrm{A}\cap\mathrm{B} \\ $$$$\left(\mathrm{A}\cup\mathrm{B}\right)\cup\mathrm{A}=\left(\mathrm{A}\cap\mathrm{B}\right)\cup\mathrm{A} \\ $$$$\mathrm{A}\cup\mathrm{B}=\mathrm{A} \\ $$$$\left(\mathrm{A}\cup\mathrm{B}\right)\cup\mathrm{B}=\left(\mathrm{A}\cap\mathrm{B}\right)\cup\mathrm{B} \\ $$$$\mathrm{A}\cup\mathrm{B}=\mathrm{B} \\ $$$$\mathrm{A}=\mathrm{B} \\ $$

Commented by 123456 last updated on 01/Sep/15

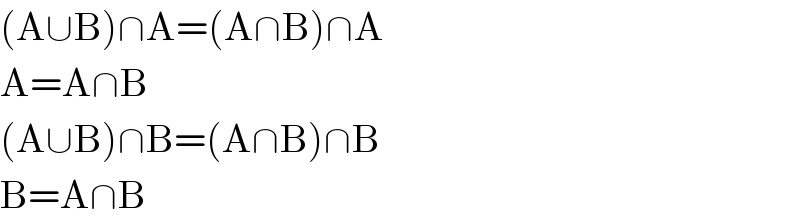
(A∪B)∩A=(A∩B)∩A A=A∩B (A∪B)∩B=(A∩B)∩B B=A∩B

$$\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{A}=\left(\mathrm{A}\cap\mathrm{B}\right)\cap\mathrm{A} \\ $$$$\mathrm{A}=\mathrm{A}\cap\mathrm{B} \\ $$$$\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{B}=\left(\mathrm{A}\cap\mathrm{B}\right)\cap\mathrm{B} \\ $$$$\mathrm{B}=\mathrm{A}\cap\mathrm{B} \\ $$

Commented by Rasheed Ahmad last updated on 01/Sep/15

G^(oo) DD_(eductio) N _!^!

$$\mathrm{G}^{{oo}} \mathrm{DD}_{\mathrm{eductio}} \mathrm{N}\:_{!} ^{!} \\ $$

Commented by 123456 last updated on 02/Sep/15

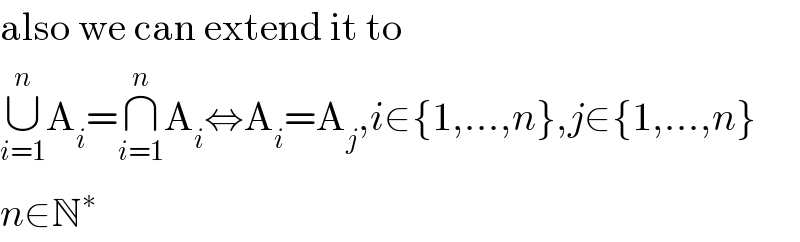
also we can extend it to ∪_(i=1) ^n A_i =∩_(i=1) ^n A_i ⇔A_i =A_j ,i∈{1,...,n},j∈{1,...,n} n∈N^∗

$$\mathrm{also}\:\mathrm{we}\:\mathrm{can}\:\mathrm{extend}\:\mathrm{it}\:\mathrm{to} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\cup}}\mathrm{A}_{{i}} =\underset{{i}=\mathrm{1}} {\overset{{n}} {\cap}}\mathrm{A}_{{i}} \Leftrightarrow\mathrm{A}_{{i}} =\mathrm{A}_{{j}} ,{i}\in\left\{\mathrm{1},...,{n}\right\},{j}\in\left\{\mathrm{1},...,{n}\right\} \\ $$$${n}\in\mathbb{N}^{\ast} \\ $$

Commented by Rasheed Soomro last updated on 03/Sep/15

Generalization! V. Good!

$${Generalization}!\:{V}.\:{Good}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com