Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 169865 by mr W last updated on 11/May/22

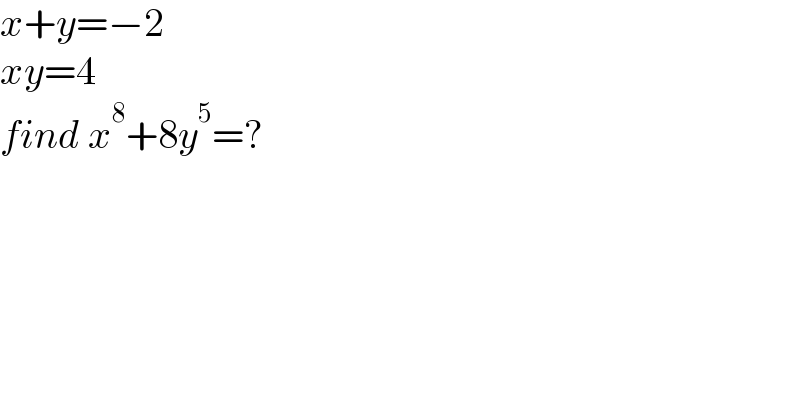
x+y=−2 xy=4 find x^8 +8y^5 =?

$${x}+{y}=−\mathrm{2} \\ $$$${xy}=\mathrm{4} \\ $$$${find}\:{x}^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} =? \\ $$

Commented by cortano1 last updated on 11/May/22

y=−x−2 ∧ x(−x−2)=4 ⇒x^2 +2x+4=0 ⇒(x+1)^2 +3 = 0 ⇒x=−1± i(√3) ⇒x=2 (−(1/2) ± ((√3)/2) i) ⇒x=−2((1/2) ∓ ((√3)/2) i)=−2e^(± i(π/3)) ⇒x^8 = 256 (cos ((8π)/3)+i sin ((8π)/3)) ⇒x^8 = 256 (cos ((2π)/3) + i sin ((2π)/3)) ⇒x^8 = 256 (−(1/2)+(1/2)(√3) i)=−128+128(√3) i ⇒y=−x−2=1∓ i(√3) −2=−1∓ i(√3) ⇒y=−2((1/2)±((√3)/2) i)=−2e^(±i (π/3)) ⇒y^5 = −32(cos ((5π)/3) ± i sin ((5π)/3)) ⇒y^5 =−32(−cos ((2π)/3) ∓ i sin ((2π)/3)) ⇒y^5 = −32((1/2) ∓ ((√3)/2) i)=−16 ± 16(√3) i ⇒8y^5 = −128 ±128(√3) i { ((x^8 +8y^5 = −256+256(√3) i)),((x^8 +8y^5 = −256)) :}

$$\:{y}=−{x}−\mathrm{2}\:\wedge\:{x}\left(−{x}−\mathrm{2}\right)=\mathrm{4} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}\:=\:\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{1}\pm\:{i}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{x}=\mathrm{2}\:\left(−\frac{\mathrm{1}}{\mathrm{2}}\:\pm\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{i}\right) \\ $$$$\Rightarrow{x}=−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\:\mp\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{i}\right)=−\mathrm{2}{e}^{\pm\:{i}\frac{\pi}{\mathrm{3}}} \\ $$$$\Rightarrow{x}^{\mathrm{8}} \:=\:\mathrm{256}\:\left(\mathrm{cos}\:\frac{\mathrm{8}\pi}{\mathrm{3}}+{i}\:\mathrm{sin}\:\frac{\mathrm{8}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{x}^{\mathrm{8}} \:=\:\mathrm{256}\:\left(\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\:{i}\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{x}^{\mathrm{8}} \:=\:\mathrm{256}\:\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\:{i}\right)=−\mathrm{128}+\mathrm{128}\sqrt{\mathrm{3}}\:{i} \\ $$$$\Rightarrow{y}=−{x}−\mathrm{2}=\mathrm{1}\mp\:{i}\sqrt{\mathrm{3}}\:−\mathrm{2}=−\mathrm{1}\mp\:{i}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{y}=−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{i}\right)=−\mathrm{2}{e}^{\pm{i}\:\frac{\pi}{\mathrm{3}}} \\ $$$$\Rightarrow{y}^{\mathrm{5}} \:=\:−\mathrm{32}\left(\mathrm{cos}\:\frac{\mathrm{5}\pi}{\mathrm{3}}\:\pm\:{i}\:\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{y}^{\mathrm{5}} =−\mathrm{32}\left(−\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:\mp\:{i}\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{y}^{\mathrm{5}} =\:−\mathrm{32}\left(\frac{\mathrm{1}}{\mathrm{2}}\:\mp\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{i}\right)=−\mathrm{16}\:\pm\:\mathrm{16}\sqrt{\mathrm{3}}\:{i} \\ $$$$\Rightarrow\mathrm{8}{y}^{\mathrm{5}} \:=\:−\mathrm{128}\:\pm\mathrm{128}\sqrt{\mathrm{3}}\:{i}\: \\ $$$$\begin{cases}{{x}^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} \:=\:−\mathrm{256}+\mathrm{256}\sqrt{\mathrm{3}}\:{i}}\\{{x}^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} \:=\:−\mathrm{256}}\end{cases} \\ $$

Commented by infinityaction last updated on 13/May/22

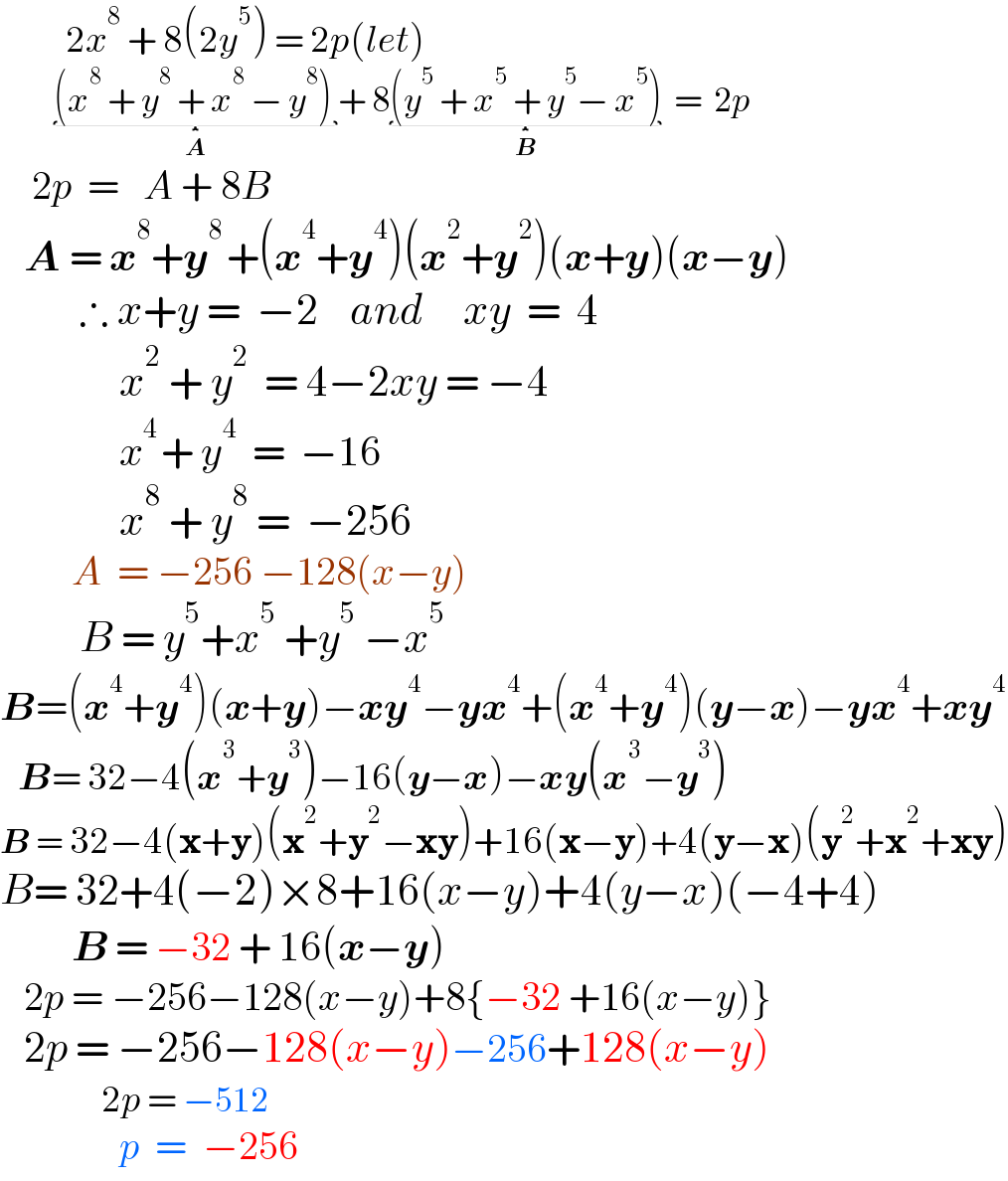
2x^8 + 8(2y^5 ) = 2p(let) (x^8 + y^8 + x^8 − y^8 ) _(A) + 8(y^5 + x^5 + y^5 − x^5 )_(B) = 2p 2p = A + 8B A = x^8 +y^(8 ) +(x^4 +y^4 )(x^2 +y^2 )(x+y)(x−y) ∴ x+y = −2 and xy = 4 x^2 + y^2 = 4−2xy = −4 x^(4 ) + y^4 = −16 x^8 + y^8 = −256 A = −256 −128(x−y) B = y^5 +x^5 +y^5 −x^5 B=(x^4 +y^4 )(x+y)−xy^4 −yx^4 +(x^4 +y^4 )(y−x)−yx^4 +xy^4 B= 32−4(x^3 +y^3 )−16(y−x)−xy(x^3 −y^3 ) B = 32−4(x+y)(x^2 +y^2 −xy)+16(x−y)+4(y−x)(y^2 +x^2 +xy) B= 32+4(−2)×8+16(x−y)+4(y−x)(−4+4) B = −32 + 16(x−y) 2p = −256−128(x−y)+8{−32 +16(x−y)} 2p = −256−128(x−y)−256+128(x−y) 2p = −512 p = −256

$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{x}^{\mathrm{8}} \:+\:\mathrm{8}\left(\mathrm{2}{y}^{\mathrm{5}} \right)\:=\:\mathrm{2}{p}\left({let}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\underset{\boldsymbol{{A}}} {\underbrace{\left({x}^{\mathrm{8}} \:+\:{y}^{\mathrm{8}} \:+\:{x}^{\mathrm{8}} \:−\:{y}^{\mathrm{8}} \right)\:}}+\:\mathrm{8}\underset{\boldsymbol{{B}}} {\underbrace{\left({y}^{\mathrm{5}} \:+\:{x}^{\mathrm{5}} \:+\:{y}^{\mathrm{5}} −\:{x}^{\mathrm{5}} \right)}}\:\:=\:\:\mathrm{2}{p} \\ $$$$\:\:\:\:\mathrm{2}{p}\:\:=\:\:\:{A}\:+\:\mathrm{8}{B} \\ $$$$\:\:\:\boldsymbol{{A}}\:=\:\boldsymbol{{x}}^{\mathrm{8}} +\boldsymbol{{y}}^{\mathrm{8}\:} +\left(\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{y}}^{\mathrm{4}} \right)\left(\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\therefore\:{x}+{y}\:=\:\:−\mathrm{2}\:\:\:\:{and}\:\:\:\:\:{xy}\:\:=\:\:\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:\:=\:\mathrm{4}−\mathrm{2}{xy}\:=\:−\mathrm{4}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{4}\:} +\:{y}^{\mathrm{4}} \:\:=\:\:−\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{8}} \:+\:{y}^{\mathrm{8}} \:=\:\:−\mathrm{256} \\ $$$$\:\:\:\:\:\:\:\:\:{A}\:\:=\:−\mathrm{256}\:−\mathrm{128}\left({x}−{y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{B}\:=\:{y}^{\mathrm{5}} +{x}^{\mathrm{5}} \:+{y}^{\mathrm{5}} \:−{x}^{\mathrm{5}} \\ $$$$\boldsymbol{{B}}=\left(\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{y}}^{\mathrm{4}} \right)\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)−\boldsymbol{{xy}}^{\mathrm{4}} −\boldsymbol{{yx}}^{\mathrm{4}} +\left(\boldsymbol{{x}}^{\mathrm{4}} +\boldsymbol{{y}}^{\mathrm{4}} \right)\left(\boldsymbol{{y}}−\boldsymbol{{x}}\right)−\boldsymbol{{yx}}^{\mathrm{4}} +\boldsymbol{{xy}}^{\mathrm{4}} \\ $$$$\:\:\:\boldsymbol{{B}}=\:\mathrm{32}−\mathrm{4}\left(\boldsymbol{{x}}^{\mathrm{3}} +\boldsymbol{{y}}^{\mathrm{3}} \right)−\mathrm{16}\left(\boldsymbol{{y}}−\boldsymbol{{x}}\right)−\boldsymbol{{xy}}\left(\boldsymbol{{x}}^{\mathrm{3}} −\boldsymbol{{y}}^{\mathrm{3}} \right) \\ $$$$\boldsymbol{{B}}\:=\:\mathrm{32}−\mathrm{4}\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\right)\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\boldsymbol{\mathrm{xy}}\right)+\mathrm{16}\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}\right)+\mathrm{4}\left(\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{x}}\right)\left(\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{xy}}\right) \\ $$$${B}=\:\mathrm{32}+\mathrm{4}\left(−\mathrm{2}\right)×\mathrm{8}+\mathrm{16}\left({x}−{y}\right)+\mathrm{4}\left({y}−{x}\right)\left(−\mathrm{4}+\mathrm{4}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{B}}\:=\:−\mathrm{32}\:+\:\mathrm{16}\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right) \\ $$$$\:\:\:\mathrm{2}{p}\:=\:−\mathrm{256}−\mathrm{128}\left({x}−{y}\right)+\mathrm{8}\left\{−\mathrm{32}\:+\mathrm{16}\left({x}−{y}\right)\right\} \\ $$$$\:\:\:\mathrm{2}{p}\:=\:−\mathrm{256}−\mathrm{128}\left({x}−{y}\right)−\mathrm{256}+\mathrm{128}\left({x}−{y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{p}\:=\:−\mathrm{512} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{p}\:\:=\:\:−\mathrm{256} \\ $$

Answered by Rasheed.Sindhi last updated on 11/May/22

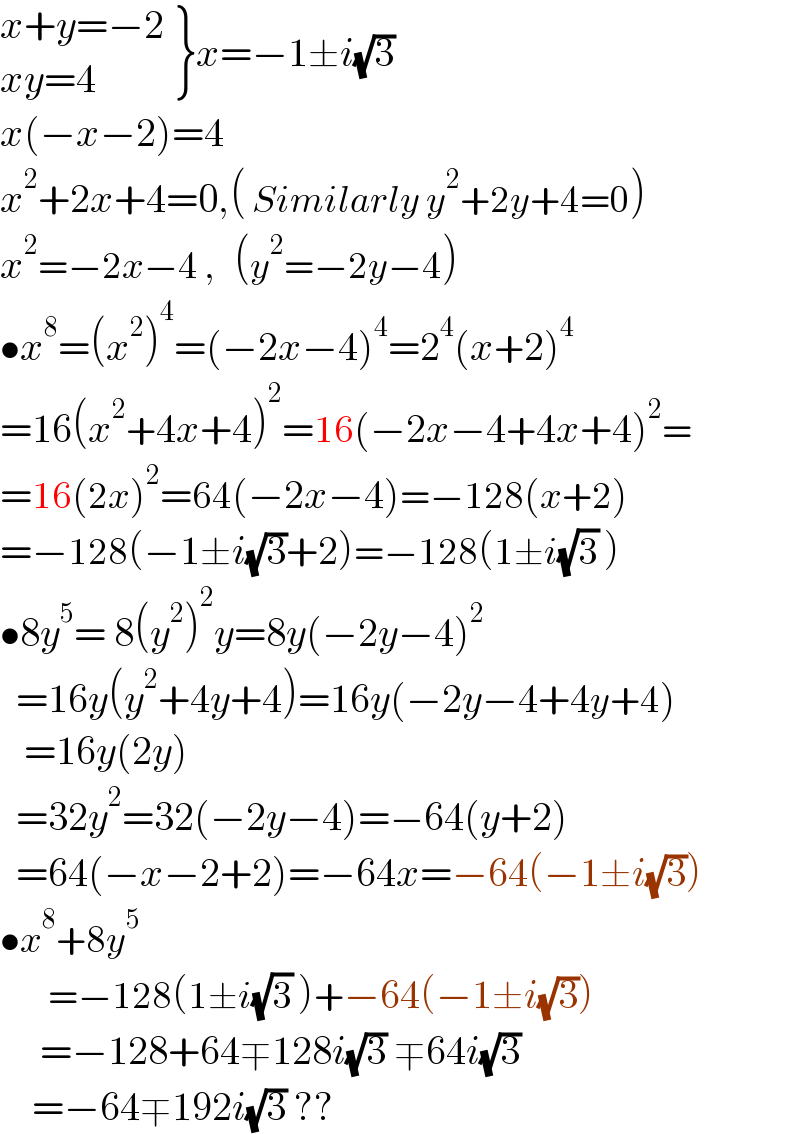
{: ((x+y=−2)),((xy=4)) }x=−1±i(√3) x(−x−2)=4 x^2 +2x+4=0,( Similarly y^2 +2y+4=0) x^2 =−2x−4 , (y^2 =−2y−4) •x^8 =(x^2 )^4 =(−2x−4)^4 =2^4 (x+2)^4 =16(x^2 +4x+4)^2 =16(−2x−4+4x+4)^2 = =16(2x)^2 =64(−2x−4)=−128(x+2) =−128(−1±i(√3)+2)=−128(1±i(√3) ) •8y^5 = 8(y^2 )^2 y=8y(−2y−4)^2 =16y(y^2 +4y+4)=16y(−2y−4+4y+4) =16y(2y) =32y^2 =32(−2y−4)=−64(y+2) =64(−x−2+2)=−64x=−64(−1±i(√3)) •x^8 +8y^5 =−128(1±i(√3) )+−64(−1±i(√3)) =−128+64∓128i(√3) ∓64i(√3) =−64∓192i(√3) ??

$$\left.\begin{matrix}{{x}+{y}=−\mathrm{2}}\\{{xy}=\mathrm{4}}\end{matrix}\right\}{x}=−\mathrm{1}\pm{i}\sqrt{\mathrm{3}} \\ $$$${x}\left(−{x}−\mathrm{2}\right)=\mathrm{4} \\ $$$${x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}=\mathrm{0},\left(\:{Similarly}\:{y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{4}=\mathrm{0}\right) \\ $$$${x}^{\mathrm{2}} =−\mathrm{2}{x}−\mathrm{4}\:,\:\:\:\left({y}^{\mathrm{2}} =−\mathrm{2}{y}−\mathrm{4}\right) \\ $$$$\bullet{x}^{\mathrm{8}} =\left({x}^{\mathrm{2}} \right)^{\mathrm{4}} =\left(−\mathrm{2}{x}−\mathrm{4}\right)^{\mathrm{4}} =\mathrm{2}^{\mathrm{4}} \left({x}+\mathrm{2}\right)^{\mathrm{4}} \\ $$$$=\mathrm{16}\left({x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}\right)^{\mathrm{2}} =\mathrm{16}\left(−\mathrm{2}{x}−\mathrm{4}+\mathrm{4}{x}+\mathrm{4}\right)^{\mathrm{2}} = \\ $$$$=\mathrm{16}\left(\mathrm{2}{x}\right)^{\mathrm{2}} =\mathrm{64}\left(−\mathrm{2}{x}−\mathrm{4}\right)=−\mathrm{128}\left({x}+\mathrm{2}\right) \\ $$$$=−\mathrm{128}\left(−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}+\mathrm{2}\right)=−\mathrm{128}\left(\mathrm{1}\pm{i}\sqrt{\mathrm{3}}\:\right) \\ $$$$\bullet\mathrm{8}{y}^{\mathrm{5}} =\:\mathrm{8}\left({y}^{\mathrm{2}} \right)^{\mathrm{2}} {y}=\mathrm{8}{y}\left(−\mathrm{2}{y}−\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\:\:=\mathrm{16}{y}\left({y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{4}\right)=\mathrm{16}{y}\left(−\mathrm{2}{y}−\mathrm{4}+\mathrm{4}{y}+\mathrm{4}\right) \\ $$$$\:\:\:=\mathrm{16}{y}\left(\mathrm{2}{y}\right) \\ $$$$\:\:=\mathrm{32}{y}^{\mathrm{2}} =\mathrm{32}\left(−\mathrm{2}{y}−\mathrm{4}\right)=−\mathrm{64}\left({y}+\mathrm{2}\right) \\ $$$$\:\:=\mathrm{64}\left(−{x}−\mathrm{2}+\mathrm{2}\right)=−\mathrm{64}{x}=−\mathrm{64}\left(−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}\right) \\ $$$$\bullet{x}^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} \\ $$$$\:\:\:\:\:\:=−\mathrm{128}\left(\mathrm{1}\pm{i}\sqrt{\mathrm{3}}\:\right)+−\mathrm{64}\left(−\mathrm{1}\pm{i}\sqrt{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:=−\mathrm{128}+\mathrm{64}\mp\mathrm{128}{i}\sqrt{\mathrm{3}}\:\mp\mathrm{64}{i}\sqrt{\mathrm{3}}\: \\ $$$$\:\:\:\:=−\mathrm{64}\mp\mathrm{192}{i}\sqrt{\mathrm{3}}\:?? \\ $$

Commented by greougoury555 last updated on 11/May/22

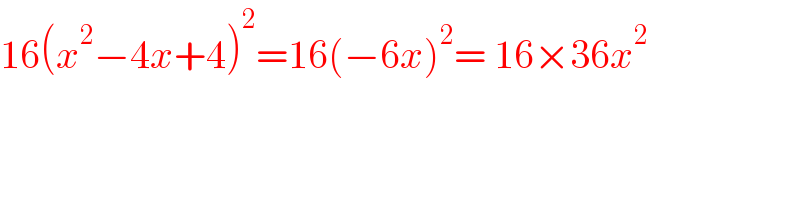
16(x^2 −4x+4)^2 =16(−6x)^2 = 16×36x^2

$$\mathrm{16}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)^{\mathrm{2}} =\mathrm{16}\left(−\mathrm{6}{x}\right)^{\mathrm{2}} =\:\mathrm{16}×\mathrm{36}{x}^{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 11/May/22

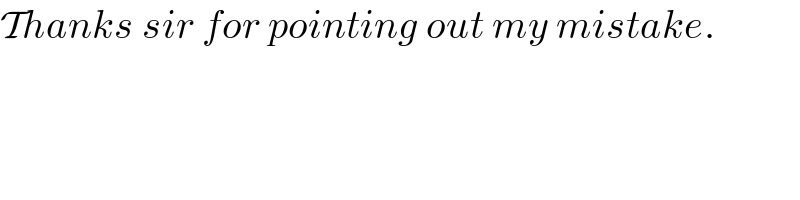
Thanks sir for pointing out my mistake.

$$\mathcal{T}{hanks}\:{sir}\:{for}\:{pointing}\:{out}\:{my}\:{mistake}. \\ $$

Answered by Rasheed.Sindhi last updated on 13/May/22

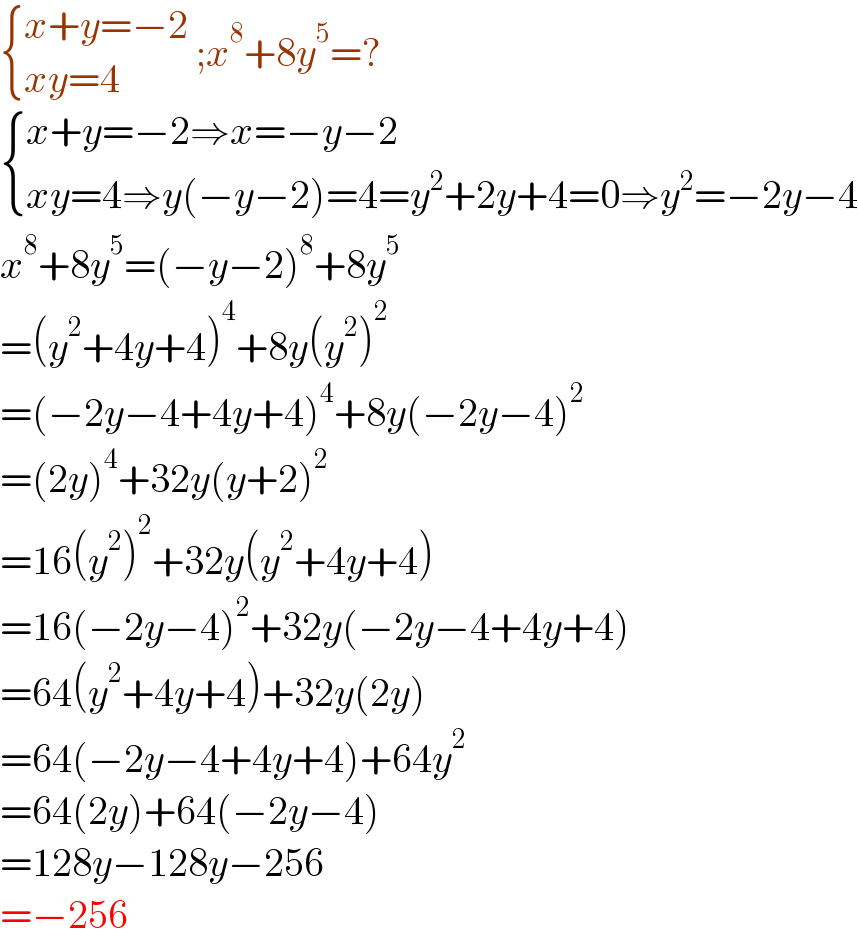
{ ((x+y=−2)),((xy=4)) :} ;x^8 +8y^5 =? { ((x+y=−2⇒x=−y−2)),((xy=4⇒y(−y−2)=4=y^2 +2y+4=0⇒y^2 =−2y−4)) :} x^8 +8y^5 =(−y−2)^8 +8y^5 =(y^2 +4y+4)^4 +8y(y^2 )^2 =(−2y−4+4y+4)^4 +8y(−2y−4)^2 =(2y)^4 +32y(y+2)^2 =16(y^2 )^2 +32y(y^2 +4y+4) =16(−2y−4)^2 +32y(−2y−4+4y+4) =64(y^2 +4y+4)+32y(2y) =64(−2y−4+4y+4)+64y^2 =64(2y)+64(−2y−4) =128y−128y−256 =−256

$$\begin{cases}{{x}+{y}=−\mathrm{2}}\\{{xy}=\mathrm{4}}\end{cases}\:;{x}^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} =? \\ $$$$\begin{cases}{{x}+{y}=−\mathrm{2}\Rightarrow{x}=−{y}−\mathrm{2}}\\{{xy}=\mathrm{4}\Rightarrow{y}\left(−{y}−\mathrm{2}\right)=\mathrm{4}={y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{4}=\mathrm{0}\Rightarrow{y}^{\mathrm{2}} =−\mathrm{2}{y}−\mathrm{4}}\end{cases} \\ $$$${x}^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} =\left(−{y}−\mathrm{2}\right)^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} \\ $$$$=\left({y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{4}\right)^{\mathrm{4}} +\mathrm{8}{y}\left({y}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$=\left(−\mathrm{2}{y}−\mathrm{4}+\mathrm{4}{y}+\mathrm{4}\right)^{\mathrm{4}} +\mathrm{8}{y}\left(−\mathrm{2}{y}−\mathrm{4}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{2}{y}\right)^{\mathrm{4}} +\mathrm{32}{y}\left({y}+\mathrm{2}\right)^{\mathrm{2}} \\ $$$$=\mathrm{16}\left({y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{32}{y}\left({y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{4}\right) \\ $$$$=\mathrm{16}\left(−\mathrm{2}{y}−\mathrm{4}\right)^{\mathrm{2}} +\mathrm{32}{y}\left(−\mathrm{2}{y}−\mathrm{4}+\mathrm{4}{y}+\mathrm{4}\right) \\ $$$$=\mathrm{64}\left({y}^{\mathrm{2}} +\mathrm{4}{y}+\mathrm{4}\right)+\mathrm{32}{y}\left(\mathrm{2}{y}\right) \\ $$$$=\mathrm{64}\left(−\mathrm{2}{y}−\mathrm{4}+\mathrm{4}{y}+\mathrm{4}\right)+\mathrm{64}{y}^{\mathrm{2}} \\ $$$$=\mathrm{64}\left(\mathrm{2}{y}\right)+\mathrm{64}\left(−\mathrm{2}{y}−\mathrm{4}\right) \\ $$$$=\mathrm{128}{y}−\mathrm{128}{y}−\mathrm{256} \\ $$$$=−\mathrm{256} \\ $$

Answered by mr W last updated on 13/May/22

x,y are roots of z^2 +2z+4=0. z^2 =−2z−4 z^3 =−2z^2 −4z=−2(−2z−4)−4z=8 i.e. x^3 =y^3 =8 x^8 +8y^5 =x^3 x^3 x^2 +8y^3 y^2 =8×8x^2 +8×8y^2 =64(x^2 +y^2 ) =64[(x+y)^2 −2xy] =64[(−2)^2 −2×4] =−64×4 =−256 ✓

$${x},{y}\:{are}\:{roots}\:{of}\:{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{4}=\mathrm{0}. \\ $$$${z}^{\mathrm{2}} =−\mathrm{2}{z}−\mathrm{4} \\ $$$${z}^{\mathrm{3}} =−\mathrm{2}{z}^{\mathrm{2}} −\mathrm{4}{z}=−\mathrm{2}\left(−\mathrm{2}{z}−\mathrm{4}\right)−\mathrm{4}{z}=\mathrm{8} \\ $$$${i}.{e}.\:{x}^{\mathrm{3}} ={y}^{\mathrm{3}} =\mathrm{8} \\ $$$$ \\ $$$${x}^{\mathrm{8}} +\mathrm{8}{y}^{\mathrm{5}} \\ $$$$={x}^{\mathrm{3}} {x}^{\mathrm{3}} {x}^{\mathrm{2}} +\mathrm{8}{y}^{\mathrm{3}} {y}^{\mathrm{2}} \\ $$$$=\mathrm{8}×\mathrm{8}{x}^{\mathrm{2}} +\mathrm{8}×\mathrm{8}{y}^{\mathrm{2}} \\ $$$$=\mathrm{64}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$=\mathrm{64}\left[\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}\right] \\ $$$$=\mathrm{64}\left[\left(−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{4}\right] \\ $$$$=−\mathrm{64}×\mathrm{4} \\ $$$$=−\mathrm{256}\:\checkmark \\ $$

Commented by infinityaction last updated on 13/May/22

great sir very nice

$${great}\:{sir}\:{very}\:{nice} \\ $$

Commented by peter frank last updated on 13/May/22

short and clear

$$\mathrm{short}\:\mathrm{and}\:\mathrm{clear} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com