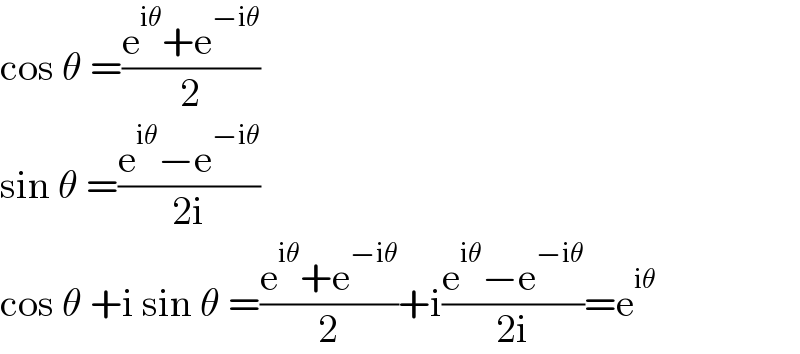Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 170110 by mathlove last updated on 16/May/22

$$provethat$$$$e^{i\theta }=cos\theta +isin\theta$$

Commented by ajfour last updated on 16/May/22

$$1\times e^{i\theta }=zis$$$$1rotatedby\theta anticlockwise.$$$$hencez=\cos \theta +i\sin \theta =e^{i\theta }$$$$drawadiagramnuknow.$$

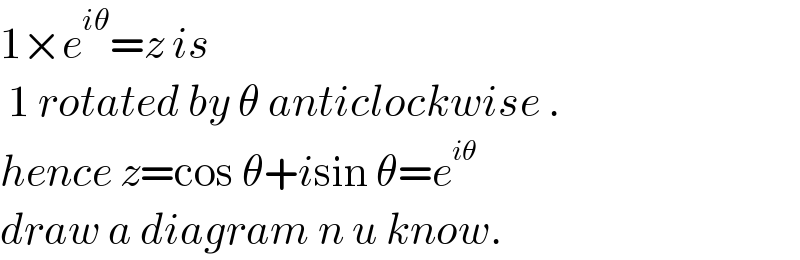
Answered by floor(10²Eta[1]) last updated on 16/May/22

$$\mathrm{using}\mathrm{the}\mathrm{mclaurin}\mathrm{series}:$$$$\mathrm{f}\left(\mathrm{x}\right)=\underset{\mathrm{n}=0}{\sum ^{\mathrm{\infty }}}\frac{{\mathrm{f}}^{\left(\mathrm{n}\right)}\left(0\right)}{\mathrm{n}!}{\mathrm{x}}^{\mathrm{n}}$$$$\mathrm{for}{\mathrm{e}}^{\mathrm{x}},\mathrm{sinx},\mathrm{cosx},\mathrm{we}\mathrm{have}:$$$${\mathrm{e}}^{\mathrm{x}}=1+\mathrm{x}+\frac{{\mathrm{x}}^2}{2!}+\frac{{\mathrm{x}}^3}{3!}+...$$$$\mathrm{sinx}=\mathrm{x}-\frac{{\mathrm{x}}^3}{3!}+\frac{{\mathrm{x}}^5}{5!}-\frac{{\mathrm{x}}^7}{7!}+...$$$$\mathrm{cosx}=1-\frac{{\mathrm{x}}^2}{2!}+\frac{{\mathrm{x}}^4}{4!}-\frac{{\mathrm{x}}^6}{6!}+...$$$$\Rightarrow {\mathrm{e}}^{\mathrm{i}\theta }=1+\mathrm{i}\theta +\frac{{\left(\mathrm{i}\theta \right)}^2}{2!}+\frac{{\left(\mathrm{i}\theta \right)}^3}{3!}+...$$$$=1+\mathrm{i}\theta -\frac{{\theta }^2}{2!}-\mathrm{i}\frac{{\theta }^3}{3!}+\frac{{\theta }^4}{4!}+\frac{\mathrm{i}{\theta }^5}{5!}-\frac{{\theta }^6}{6!}-\frac{\mathrm{i}{\theta }^7}{7!}+...$$$$=(1-\frac{{\theta }^2}{2!}+\frac{{\theta }^4}{4!}-\frac{{\theta }^6}{6!}+...)+\mathrm{i}(\theta -\frac{{\theta }^3}{3!}+\frac{{\theta }^5}{5!}-\frac{{\theta }^7}{7!}+...)$$$$=\cos \theta +\mathrm{isin}\theta$$$$$$

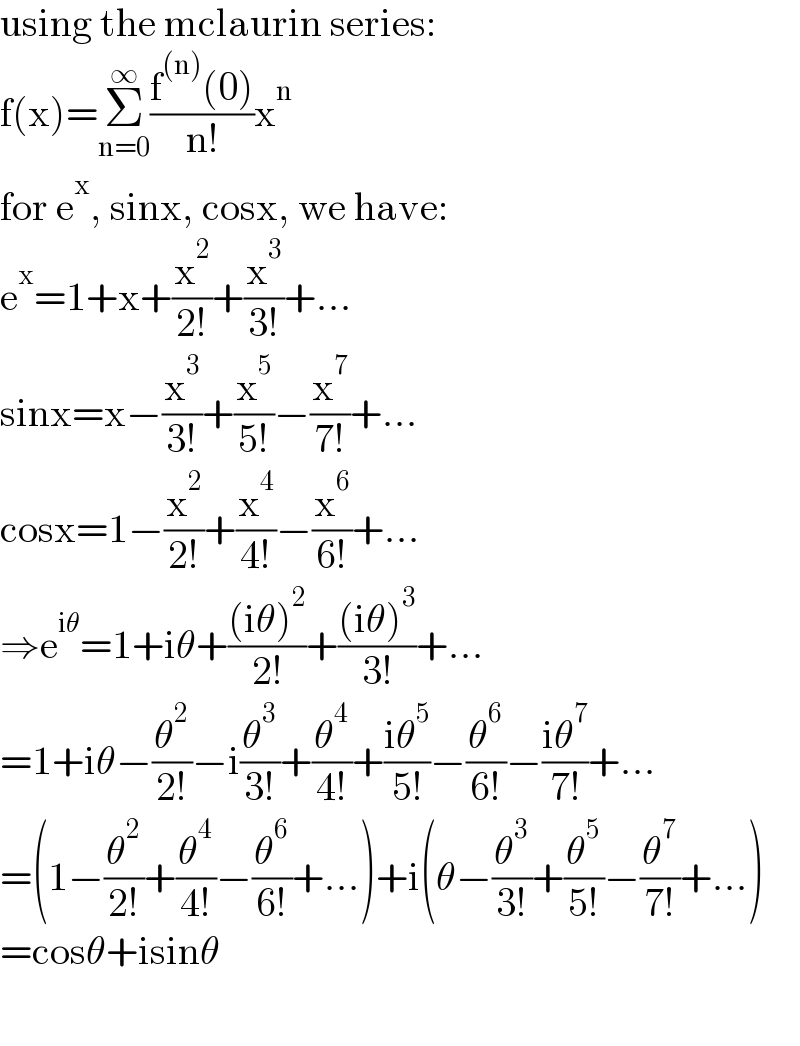
Commented by peter frank last updated on 16/May/22

$$\mathrm{thank}\mathrm{you}$$

Commented by mathlove last updated on 16/May/22

$$thanks$$

Answered by MJS_new last updated on 18/May/22

$$\cos \theta =\frac{{\mathrm{e}}^{\mathrm{i}\theta }+{\mathrm{e}}^{-\mathrm{i}\theta }}{2}$$$$\sin \theta =\frac{{\mathrm{e}}^{\mathrm{i}\theta }-{\mathrm{e}}^{-\mathrm{i}\theta }}{2\mathrm{i}}$$$$\cos \theta +\mathrm{i}\sin \theta =\frac{{\mathrm{e}}^{\mathrm{i}\theta }+{\mathrm{e}}^{-\mathrm{i}\theta }}{2}+\mathrm{i}\frac{{\mathrm{e}}^{\mathrm{i}\theta }-{\mathrm{e}}^{-\mathrm{i}\theta }}{2\mathrm{i}}={\mathrm{e}}^{\mathrm{i}\theta }$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com