Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 170141 by sciencestudent last updated on 17/May/22

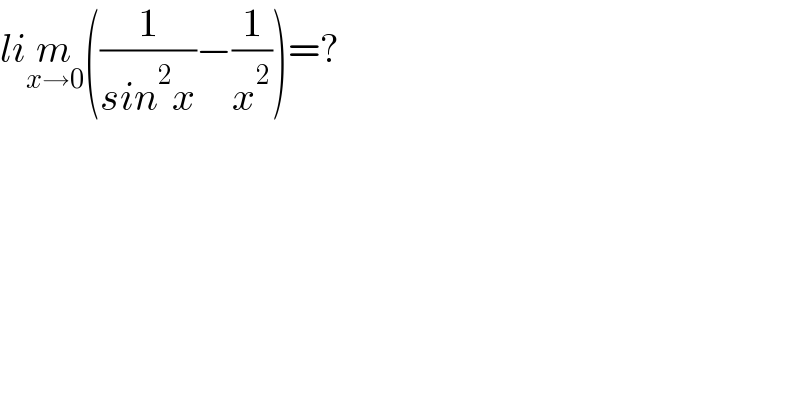
lim_(x→0) ((1/(sin^2 x))−(1/x^2 ))=?

$${li}\underset{{x}\rightarrow\mathrm{0}} {{m}}\left(\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)=? \\ $$

Commented by mr W last updated on 17/May/22

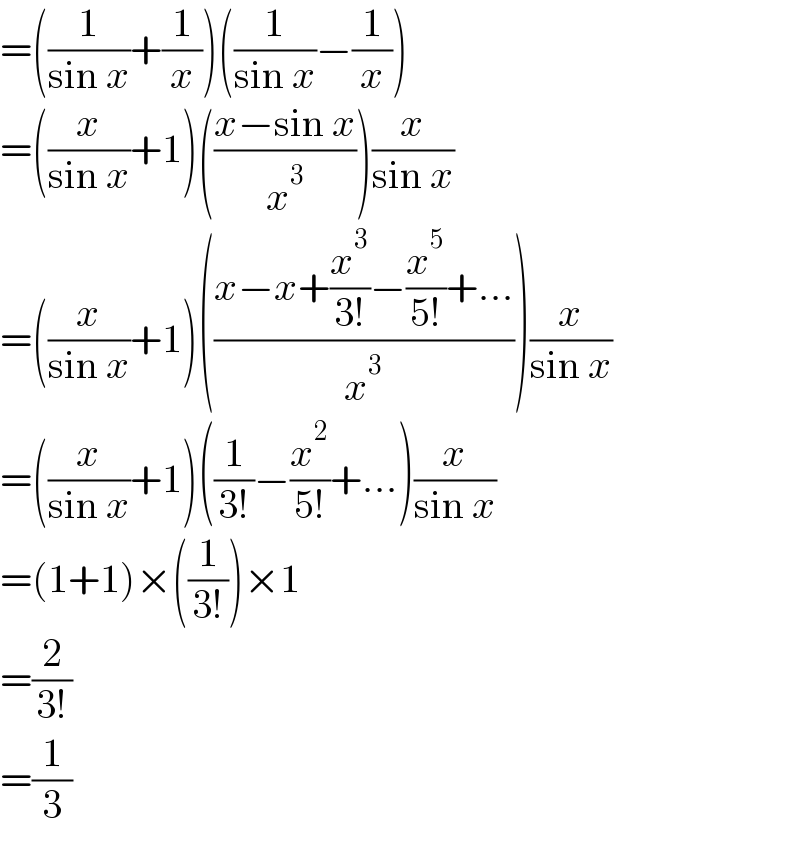
=((1/(sin x))+(1/x))((1/(sin x))−(1/x)) =((x/(sin x))+1)(((x−sin x)/x^3 ))(x/(sin x)) =((x/(sin x))+1)(((x−x+(x^3 /(3!))−(x^5 /(5!))+...)/x^3 ))(x/(sin x)) =((x/(sin x))+1)((1/(3!))−(x^2 /(5!))+...)(x/(sin x)) =(1+1)×((1/(3!)))×1 =(2/(3!)) =(1/3)

$$=\left(\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{{x}}\right)\left(\frac{\mathrm{1}}{\mathrm{sin}\:{x}}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$=\left(\frac{{x}}{\mathrm{sin}\:{x}}+\mathrm{1}\right)\left(\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{3}} }\right)\frac{{x}}{\mathrm{sin}\:{x}} \\ $$$$=\left(\frac{{x}}{\mathrm{sin}\:{x}}+\mathrm{1}\right)\left(\frac{{x}−{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}+...}{{x}^{\mathrm{3}} }\right)\frac{{x}}{\mathrm{sin}\:{x}} \\ $$$$=\left(\frac{{x}}{\mathrm{sin}\:{x}}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{3}!}−\frac{{x}^{\mathrm{2}} }{\mathrm{5}!}+...\right)\frac{{x}}{\mathrm{sin}\:{x}} \\ $$$$=\left(\mathrm{1}+\mathrm{1}\right)×\left(\frac{\mathrm{1}}{\mathrm{3}!}\right)×\mathrm{1} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}!} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by sciencestudent last updated on 17/May/22

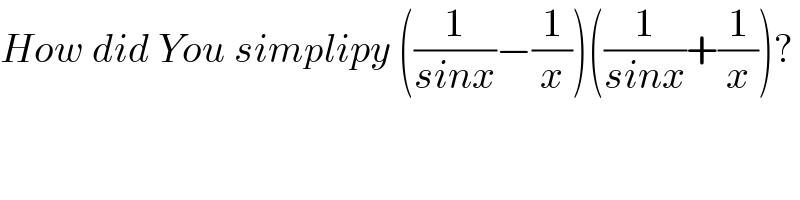
How did You simplipy ((1/(sinx))−(1/x))((1/(sinx))+(1/x))?

$${How}\:{did}\:{You}\:{simplipy}\:\left(\frac{\mathrm{1}}{{sinx}}−\frac{\mathrm{1}}{{x}}\right)\left(\frac{\mathrm{1}}{{sinx}}+\frac{\mathrm{1}}{{x}}\right)? \\ $$

Commented by mr W last updated on 17/May/22

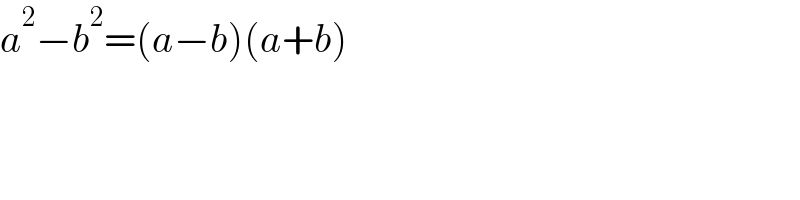
a^2 −b^2 =(a−b)(a+b)

$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} =\left({a}−{b}\right)\left({a}+{b}\right) \\ $$

Answered by ajfour last updated on 17/May/22

l=lim_(x→0) ((2/(1−cos 2x))−(1/x^2 )) =lim_(x→0) ((2/(1−[1−((4x^2 )/(2!))+((16x^4 )/(4!))−..]))−(1/x^2 )) =lim_(x→0) (1/x^2 )((/(1−((1x^2 )/3)+sx^4 −..))−1) =lim_(x→0) ((((1/3)−sx^2 +...)/(1−(x^2 /3)+sx^4 −...)))=(1/3)

$${l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}}{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}}{\mathrm{1}−\left[\mathrm{1}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{\mathrm{16}{x}^{\mathrm{4}} }{\mathrm{4}!}−..\right]}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\left(\frac{}{\mathrm{1}−\frac{\mathrm{1}{x}^{\mathrm{2}} }{\mathrm{3}}+{sx}^{\mathrm{4}} −..}−\mathrm{1}\right) \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\frac{\mathrm{1}}{\mathrm{3}}−{sx}^{\mathrm{2}} +...}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+{sx}^{\mathrm{4}} −...}\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by sciencestudent last updated on 17/May/22

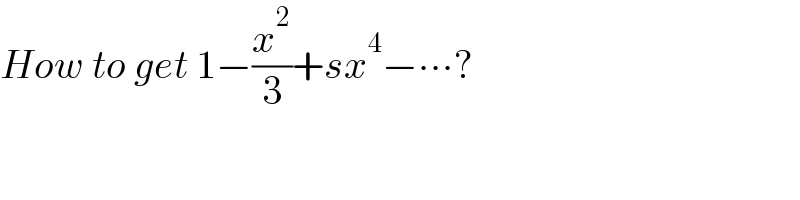
How to get 1−(x^2 /3)+sx^4 −∙∙∙?

$${How}\:{to}\:{get}\:\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{3}}+{sx}^{\mathrm{4}} −\centerdot\centerdot\centerdot? \\ $$

Commented by mr W last updated on 17/May/22

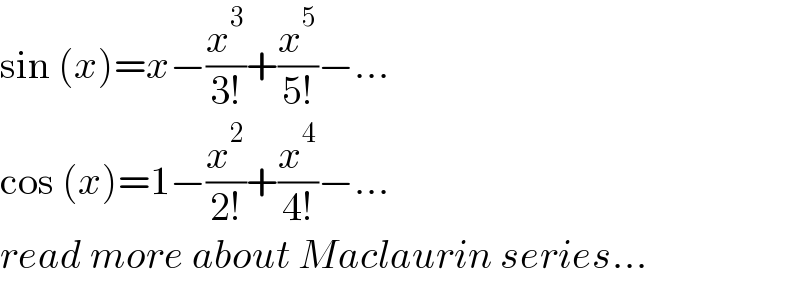
sin (x)=x−(x^3 /(3!))+(x^5 /(5!))−... cos (x)=1−(x^2 /(2!))+(x^4 /(4!))−... read more about Maclaurin series...

$$\mathrm{sin}\:\left({x}\right)={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}−... \\ $$$$\mathrm{cos}\:\left({x}\right)=\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}−... \\ $$$${read}\:{more}\:{about}\:{Maclaurin}\:{series}... \\ $$

Commented by mr W last updated on 17/May/22

Terms of Service

Privacy Policy

Contact: info@tinkutara.com