
Question Number 17018 by tawa tawa last updated on 29/Jun/17
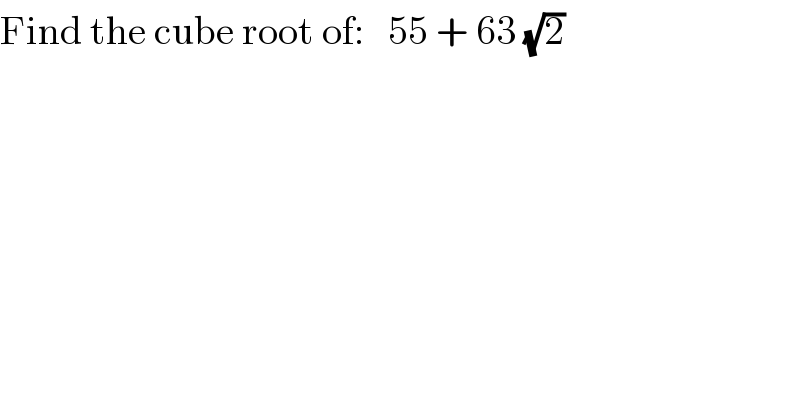
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}:\:\:\:\mathrm{55}\:+\:\mathrm{63}\:\sqrt{\mathrm{2}} \\ $$
Commented by prakash jain last updated on 29/Jun/17
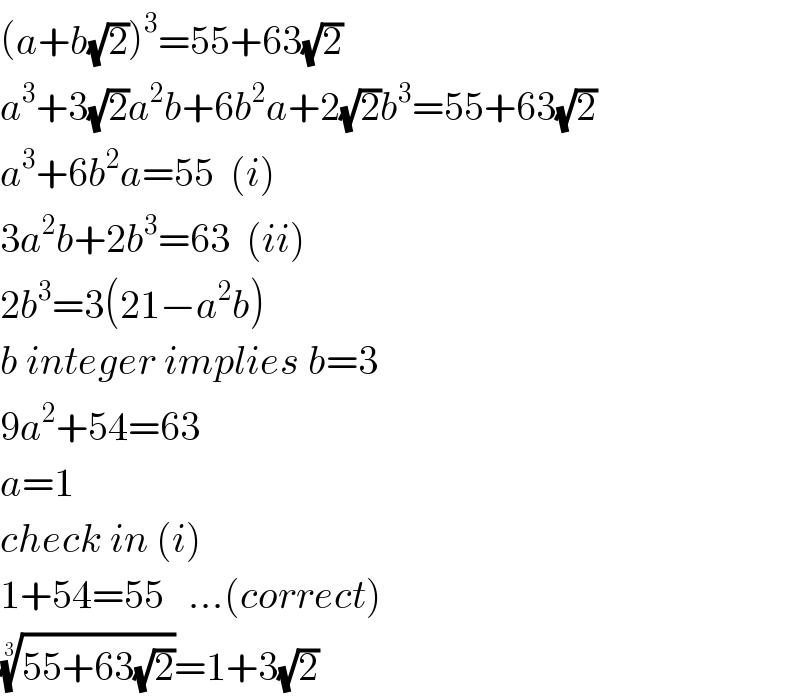
$$\left({a}+{b}\sqrt{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{55}+\mathrm{63}\sqrt{\mathrm{2}} \\ $$$${a}^{\mathrm{3}} +\mathrm{3}\sqrt{\mathrm{2}}{a}^{\mathrm{2}} {b}+\mathrm{6}{b}^{\mathrm{2}} {a}+\mathrm{2}\sqrt{\mathrm{2}}{b}^{\mathrm{3}} =\mathrm{55}+\mathrm{63}\sqrt{\mathrm{2}} \\ $$$${a}^{\mathrm{3}} +\mathrm{6}{b}^{\mathrm{2}} {a}=\mathrm{55}\:\:\left({i}\right) \\ $$$$\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{2}{b}^{\mathrm{3}} =\mathrm{63}\:\:\left({ii}\right) \\ $$$$\mathrm{2}{b}^{\mathrm{3}} =\mathrm{3}\left(\mathrm{21}−{a}^{\mathrm{2}} {b}\right) \\ $$$${b}\:{integer}\:{implies}\:{b}=\mathrm{3}\: \\ $$$$\mathrm{9}{a}^{\mathrm{2}} +\mathrm{54}=\mathrm{63} \\ $$$${a}=\mathrm{1} \\ $$$${check}\:{in}\:\left({i}\right) \\ $$$$\mathrm{1}+\mathrm{54}=\mathrm{55}\:\:\:...\left({correct}\right) \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{55}+\mathrm{63}\sqrt{\mathrm{2}}}=\mathrm{1}+\mathrm{3}\sqrt{\mathrm{2}} \\ $$
Commented by tawa tawa last updated on 29/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 30/Jun/17
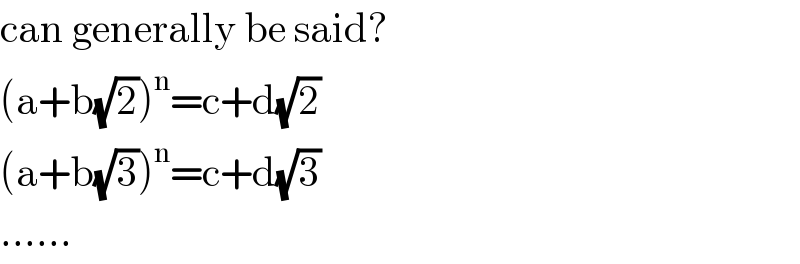
$$\mathrm{can}\:\mathrm{generally}\:\mathrm{be}\:\mathrm{said}? \\ $$$$\left(\mathrm{a}+\mathrm{b}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} =\mathrm{c}+\mathrm{d}\sqrt{\mathrm{2}} \\ $$$$\left(\mathrm{a}+\mathrm{b}\sqrt{\mathrm{3}}\right)^{\mathrm{n}} =\mathrm{c}+\mathrm{d}\sqrt{\mathrm{3}} \\ $$$$...... \\ $$
Commented by prakash jain last updated on 30/Jun/17

$$\mathrm{Not}\:\mathrm{always}. \\ $$
Commented by prakash jain last updated on 30/Jun/17

$$\mathrm{if}\:\mathrm{we}\:\mathrm{change}\:\mathrm{the}\:\mathrm{question}\:\mathrm{to} \\ $$$$\mathrm{55}+\mathrm{62}\sqrt{\mathrm{2}}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{wont}\:\mathrm{be} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{form}\:{a}+{b}\sqrt{\mathrm{2}}. \\ $$$$\mathrm{i}\:\mathrm{just}\:\mathrm{tried}\:\mathrm{this}\:\mathrm{approach}\:\mathrm{just} \\ $$$$\mathrm{to}\:\mathrm{see}\:\mathrm{if}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{possible}. \\ $$
Commented by mrW1 last updated on 30/Jun/17
![is (a+b(√2))^n not always of the form c+d(√2) ? (a+b(√2))^n =Σ_(k=0) ^n C_n ^k a^(n−k) (b(√2))^k =C_n ^0 a^n +C_n ^2 a^(n−2) b^2 ((√2))^2 +C_n ^4 a^(n−4) b^4 ((√2))^4 +... +C_n ^1 a^(n−1) b((√2))+C_n ^3 a^(n−3) b^3 ((√2))^3 +C_n ^5 a^(n−5) b^5 ((√2))^5 +... =C_n ^0 a^n +2C_n ^2 a^(n−2) b^2 +2^2 C_n ^4 a^(n−4) b^4 +... +C_n ^1 a^(n−1) b(√2)+2C_n ^3 a^(n−3) b^3 (√2)+2^2 C_n ^5 a^(n−5) b^5 (√2)+... =[C_n ^0 a^n +2C_n ^2 a^(n−2) b^2 +2^2 C_n ^4 a^(n−4) b^4 +...] +[C_n ^1 a^(n−1) b+2C_n ^3 a^(n−3) b^3 +2^2 C_n ^5 a^(n−5) b^5 +...](√2) =c+d(√2) a,b,c,d=integer](Q17109.png)
$$\mathrm{is}\:\left(\mathrm{a}+\mathrm{b}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} \:\mathrm{not}\:\mathrm{always}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form} \\ $$$$\mathrm{c}+\mathrm{d}\sqrt{\mathrm{2}}\:? \\ $$$$\left(\mathrm{a}+\mathrm{b}\sqrt{\mathrm{2}}\right)^{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{a}^{\mathrm{n}−\mathrm{k}} \left(\mathrm{b}\sqrt{\mathrm{2}}\right)^{\mathrm{k}} \\ $$$$=\mathrm{C}_{\mathrm{n}} ^{\mathrm{0}} \mathrm{a}^{\mathrm{n}} +\mathrm{C}_{\mathrm{n}} ^{\mathrm{2}} \mathrm{a}^{\mathrm{n}−\mathrm{2}} \mathrm{b}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{C}_{\mathrm{n}} ^{\mathrm{4}} \mathrm{a}^{\mathrm{n}−\mathrm{4}} \mathrm{b}^{\mathrm{4}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{4}} +... \\ $$$$+\mathrm{C}_{\mathrm{n}} ^{\mathrm{1}} \mathrm{a}^{\mathrm{n}−\mathrm{1}} \mathrm{b}\left(\sqrt{\mathrm{2}}\right)+\mathrm{C}_{\mathrm{n}} ^{\mathrm{3}} \mathrm{a}^{\mathrm{n}−\mathrm{3}} \mathrm{b}^{\mathrm{3}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{3}} +\mathrm{C}_{\mathrm{n}} ^{\mathrm{5}} \mathrm{a}^{\mathrm{n}−\mathrm{5}} \mathrm{b}^{\mathrm{5}} \left(\sqrt{\mathrm{2}}\right)^{\mathrm{5}} +... \\ $$$$=\mathrm{C}_{\mathrm{n}} ^{\mathrm{0}} \mathrm{a}^{\mathrm{n}} +\mathrm{2C}_{\mathrm{n}} ^{\mathrm{2}} \mathrm{a}^{\mathrm{n}−\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{4}} \mathrm{a}^{\mathrm{n}−\mathrm{4}} \mathrm{b}^{\mathrm{4}} +... \\ $$$$+\mathrm{C}_{\mathrm{n}} ^{\mathrm{1}} \mathrm{a}^{\mathrm{n}−\mathrm{1}} \mathrm{b}\sqrt{\mathrm{2}}+\mathrm{2C}_{\mathrm{n}} ^{\mathrm{3}} \mathrm{a}^{\mathrm{n}−\mathrm{3}} \mathrm{b}^{\mathrm{3}} \sqrt{\mathrm{2}}+\mathrm{2}^{\mathrm{2}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{5}} \mathrm{a}^{\mathrm{n}−\mathrm{5}} \mathrm{b}^{\mathrm{5}} \sqrt{\mathrm{2}}+... \\ $$$$=\left[\mathrm{C}_{\mathrm{n}} ^{\mathrm{0}} \mathrm{a}^{\mathrm{n}} +\mathrm{2C}_{\mathrm{n}} ^{\mathrm{2}} \mathrm{a}^{\mathrm{n}−\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{4}} \mathrm{a}^{\mathrm{n}−\mathrm{4}} \mathrm{b}^{\mathrm{4}} +...\right] \\ $$$$+\left[\mathrm{C}_{\mathrm{n}} ^{\mathrm{1}} \mathrm{a}^{\mathrm{n}−\mathrm{1}} \mathrm{b}+\mathrm{2C}_{\mathrm{n}} ^{\mathrm{3}} \mathrm{a}^{\mathrm{n}−\mathrm{3}} \mathrm{b}^{\mathrm{3}} +\mathrm{2}^{\mathrm{2}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{5}} \mathrm{a}^{\mathrm{n}−\mathrm{5}} \mathrm{b}^{\mathrm{5}} +...\right]\sqrt{\mathrm{2}} \\ $$$$=\mathrm{c}+\mathrm{d}\sqrt{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}=\mathrm{integer} \\ $$
Commented by mrW1 last updated on 30/Jun/17
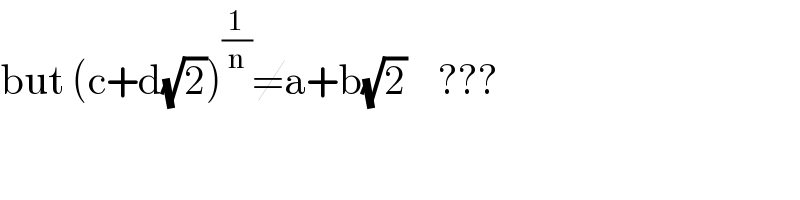
$$\mathrm{but}\:\left(\mathrm{c}+\mathrm{d}\sqrt{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \neq\mathrm{a}+\mathrm{b}\sqrt{\mathrm{2}}\:\:\:\:??? \\ $$
Commented by tawa tawa last updated on 30/Jun/17
$$\mathrm{Thanks}\:\mathrm{sirs}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
