
Question and Answers Forum
Question Number 170211 by mathlove last updated on 18/May/22
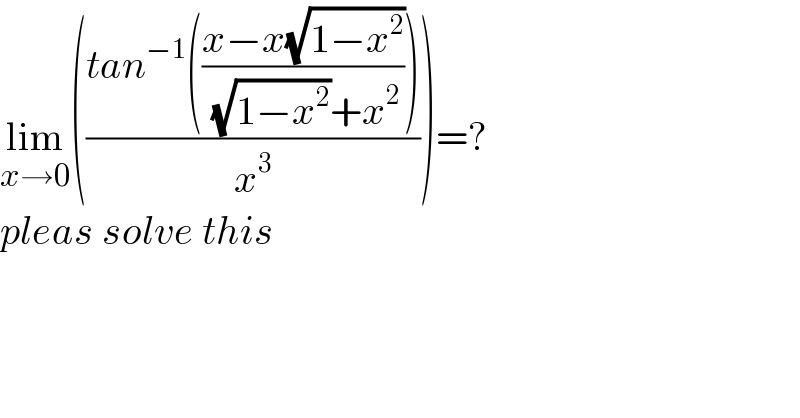
Answered by aleks041103 last updated on 18/May/22
![1) lim_(x→0) ((arctan x)/x) =^(L′H) lim_(x→0) (1/(1+x^2 ))=1 2) lim_(x→0) ((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))=0 3) ⇒lim_(x→0) (((tan^(−1) (((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))))/x^3 ))= =[lim_(x→0) (((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))/x^3 )][lim_(y→0) ((arctan(y))/y)]= =lim_(x→0) (((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))/x^3 ) where y=((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 )) 4) ⇒L=lim_(x→0) ((x(1−(√(1−x^2 ))))/(x^3 (x^2 +(√(1−x^2 )))))= =(lim_(x→0) (1/(x^2 +(√(1−x^2 )))))(lim_(x→0) ((1−(√(1−x^2 )))/x^2 )) =lim_(x→0) ((1−(√(1−x^2 )))/x^2 )=lim_(x→0) (((1−(√(1−x^2 )))(1+(√(1−x^2 ))))/(x^2 (1+(√(1−x^2 )))))= =lim_(x→0) ((1−(1−x^2 ))/(x^2 (1+(√(1−x^2 )))))=lim_(x→0) (1/(1+(√(1−x^2 ))))=(1/2) ⇒Ans. (1/2)](Q170216.png)
Commented by mathlove last updated on 18/May/22

| ||
Question and Answers Forum | ||
Question Number 170211 by mathlove last updated on 18/May/22 | ||
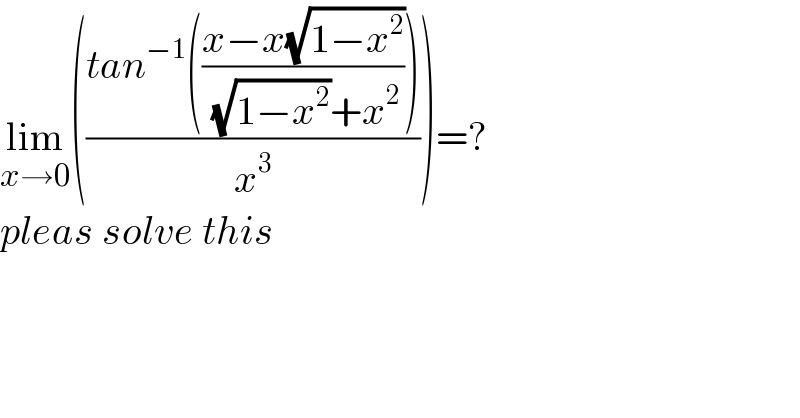 | ||
Answered by aleks041103 last updated on 18/May/22 | ||
![1) lim_(x→0) ((arctan x)/x) =^(L′H) lim_(x→0) (1/(1+x^2 ))=1 2) lim_(x→0) ((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))=0 3) ⇒lim_(x→0) (((tan^(−1) (((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))))/x^3 ))= =[lim_(x→0) (((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))/x^3 )][lim_(y→0) ((arctan(y))/y)]= =lim_(x→0) (((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 ))/x^3 ) where y=((x−x(√(1−x^2 )))/( (√(1−x^2 ))+x^2 )) 4) ⇒L=lim_(x→0) ((x(1−(√(1−x^2 ))))/(x^3 (x^2 +(√(1−x^2 )))))= =(lim_(x→0) (1/(x^2 +(√(1−x^2 )))))(lim_(x→0) ((1−(√(1−x^2 )))/x^2 )) =lim_(x→0) ((1−(√(1−x^2 )))/x^2 )=lim_(x→0) (((1−(√(1−x^2 )))(1+(√(1−x^2 ))))/(x^2 (1+(√(1−x^2 )))))= =lim_(x→0) ((1−(1−x^2 ))/(x^2 (1+(√(1−x^2 )))))=lim_(x→0) (1/(1+(√(1−x^2 ))))=(1/2) ⇒Ans. (1/2)](Q170216.png) | ||
| ||
Commented by mathlove last updated on 18/May/22 | ||
 | ||