Question Number 170336 by Mastermind last updated on 21/May/22
$${if}\:{cos}^{\mathrm{2}} \propto\:+\:\mathrm{3}{cosec}^{\mathrm{2}} \theta\:=\:\mathrm{7},\:{find}\:{the}\: \\ $$$${expression}\:{of}\:{tan}^{\mathrm{2}} \theta,\:{Hence}\:{show}\:{that} \\ $$$${tan}\theta=\mathrm{1}. \\ $$$$ \\ $$$${Mastermind} \\ $$
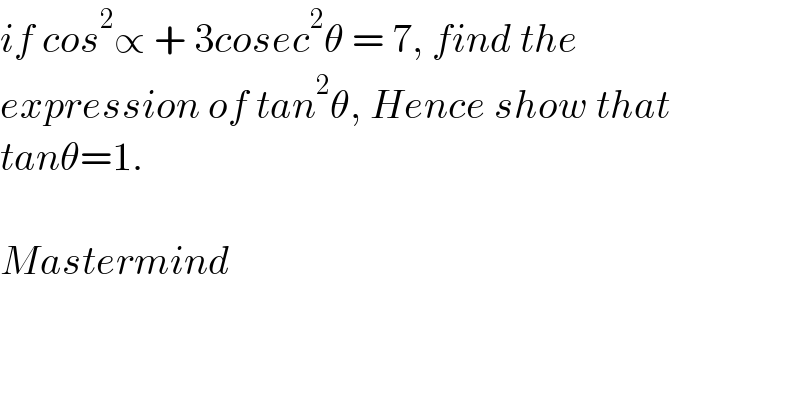
Commented by MATHSLORD22 last updated on 21/May/22
$$\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{or}\:\mathrm{cos}^{\mathrm{2}} \alpha\:?? \\ $$
Answered by thfchristopher last updated on 21/May/22
$$\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{3csc}^{\mathrm{2}} \theta=\mathrm{7} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{3}=\mathrm{7sin}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \theta\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)+\mathrm{3}=\mathrm{7sin}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{3}=\mathrm{7sin}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{6sin}^{\mathrm{2}} \theta−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{sin}^{\mathrm{2}} \theta=\frac{−\mathrm{6}\pm\sqrt{\mathrm{36}+\mathrm{12}}}{\mathrm{2}}=\frac{−\mathrm{6}\pm\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\therefore\:\mathrm{sin}^{\mathrm{2}} \theta=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \theta=\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{2}} \theta=\frac{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
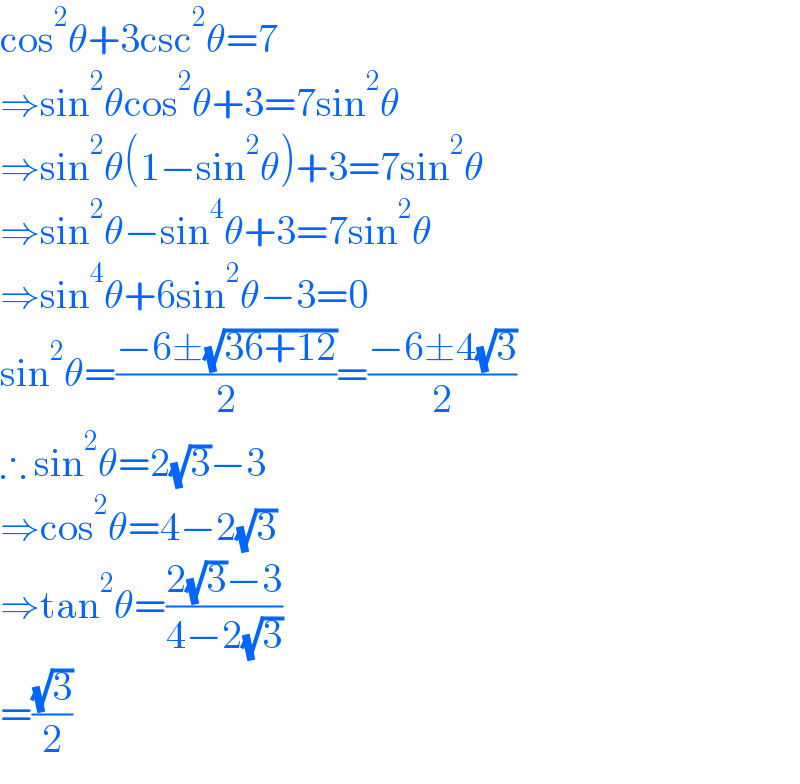
Commented by MATHSLORD22 last updated on 21/May/22
$$\mathrm{He}\:\mathrm{wrote}\:\alpha\:\mathrm{not}\:\theta \\ $$
Commented by mr W last updated on 21/May/22
$$\left.\mathrm{He}\:\mathrm{wrote}\:\propto\:\mathrm{not}\:\alpha\::\right) \\ $$
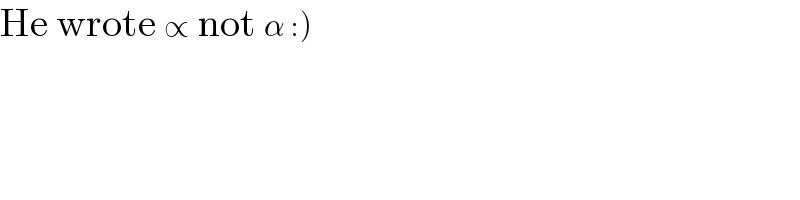
Commented by Mastermind last updated on 21/May/22
$${Thank}\:{you}\:{man} \\ $$
Answered by 2kdw last updated on 28/Apr/23
![i) cos^2 α +(3/(sin^2 α))=7 if cos^2 x=1−sin^2 x ...(1) and sin^2 x=t ... (2) ∴ t(1−t)+3=7t −t^2 +t+3=7t −t^2 −6t+3=0 ∴ (t+3)^2 =12 ⇒t=2(√3)−3 or t=−3−2(√3) but (1) 1−t≥0 then t≤1 ∴ determinant (((t=2(√3)−3))) ii) If (2) t=sin^2 α [sin^2 α=2(√3)−3] ...(1) cos^2 α=1−2(√3)+3 ∴ tan^2 α=((2(√3)−3)/(1−2(√3)+3)) determinant (((tan^2 α=((2(√3)−3)/(4−2(√3))))))](Q170354.png)
$$\left.{i}\right)\:{cos}^{\mathrm{2}} \alpha\:+\frac{\mathrm{3}}{{sin}^{\mathrm{2}} \alpha}=\mathrm{7} \\ $$$$ \\ $$$${if}\:{cos}^{\mathrm{2}} {x}=\mathrm{1}−{sin}^{\mathrm{2}} {x}\:\:...\left(\mathrm{1}\right) \\ $$$${and}\:{sin}^{\mathrm{2}} {x}={t}\:...\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\therefore\:{t}\left(\mathrm{1}−{t}\right)+\mathrm{3}=\mathrm{7}{t} \\ $$$$−{t}^{\mathrm{2}} +{t}+\mathrm{3}=\mathrm{7}{t} \\ $$$$−{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{3}=\mathrm{0} \\ $$$$\therefore\:\left({t}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{12} \\ $$$$\Rightarrow{t}=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}\:{or}\:{t}=−\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${but}\:\:\:\left(\mathrm{1}\right)\:\:\:\mathrm{1}−{t}\geqslant\mathrm{0}\:\:\:\:{then}\:\:{t}\leqslant\mathrm{1} \\ $$$$\therefore\:\begin{array}{|c|}{{t}=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}\\\hline\end{array} \\ $$$$ \\ $$$$\left.{ii}\right)\:{If}\:\left(\mathrm{2}\right)\:\:{t}={sin}^{\mathrm{2}} \alpha \\ $$$$\left[{sin}^{\mathrm{2}} \alpha=\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}\right] \\ $$$$ \\ $$$$...\left(\mathrm{1}\right)\:\:{cos}^{\mathrm{2}} \alpha=\mathrm{1}−\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3} \\ $$$$ \\ $$$$ \\ $$$$\therefore\:\:{tan}^{\mathrm{2}} \alpha=\frac{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}} \\ $$$$ \\ $$$$\begin{array}{|c|}{{tan}^{\mathrm{2}} \alpha=\frac{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}}\\\hline\end{array} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Mastermind last updated on 21/May/22
$${Thanks}\:{man} \\ $$