Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 170426 by daus last updated on 23/May/22

Answered by Rasheed.Sindhi last updated on 23/May/22

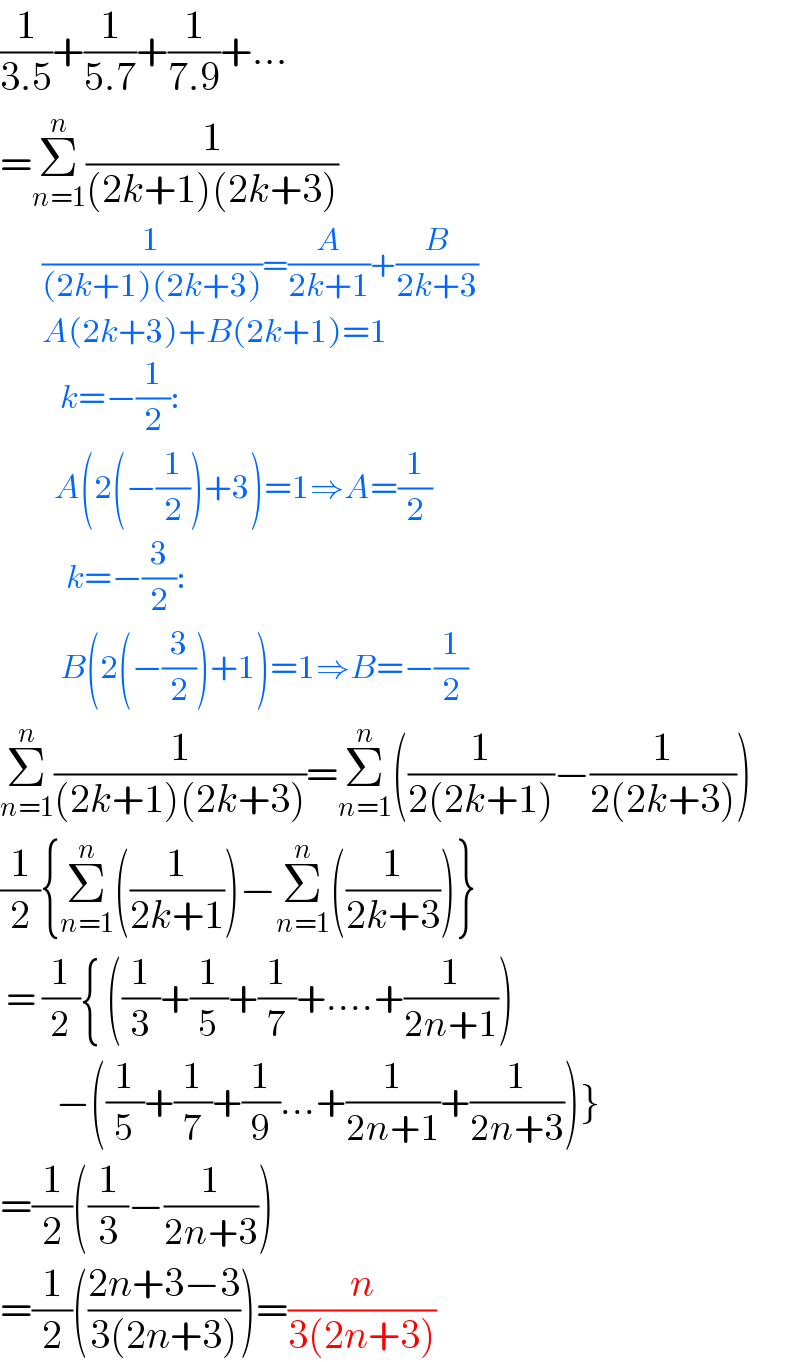
(1/(3.5))+(1/(5.7))+(1/(7.9))+... =Σ_(n=1) ^n (1/((2k+1)(2k+3))) (1/((2k+1)(2k+3)))=(A/(2k+1))+(B/(2k+3)) A(2k+3)+B(2k+1)=1 k=−(1/2): A(2(−(1/2))+3)=1⇒A=(1/2) k=−(3/2): B(2(−(3/2))+1)=1⇒B=−(1/2) Σ_(n=1) ^n (1/((2k+1)(2k+3)))=Σ_(n=1) ^n ((1/(2(2k+1)))−(1/(2(2k+3)))) (1/2){Σ_(n=1) ^n ((1/(2k+1)))−Σ_(n=1) ^n ((1/(2k+3)))} = (1/2){ ((1/3)+(1/5)+(1/7)+....+(1/(2n+1))) −((1/5)+(1/7)+(1/9)...+(1/(2n+1))+(1/(2n+3)))} =(1/2)((1/3)−(1/(2n+3))) =(1/2)(((2n+3−3)/(3(2n+3))))=(n/(3(2n+3)))

$$\frac{\mathrm{1}}{\mathrm{3}.\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}.\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{7}.\mathrm{9}}+... \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)} \\ $$$$\:\:\:\:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)}=\frac{{A}}{\mathrm{2}{k}+\mathrm{1}}+\frac{{B}}{\mathrm{2}{k}+\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:{A}\left(\mathrm{2}{k}+\mathrm{3}\right)+{B}\left(\mathrm{2}{k}+\mathrm{1}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:{k}=−\frac{\mathrm{1}}{\mathrm{2}}: \\ $$$$\:\:\:\:\:\:\:\:\:{A}\left(\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3}\right)=\mathrm{1}\Rightarrow{A}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{k}=−\frac{\mathrm{3}}{\mathrm{2}}: \\ $$$$\:\:\:\:\:\:\:\:\:\:{B}\left(\mathrm{2}\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{1}\right)=\mathrm{1}\Rightarrow{B}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)}=\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{k}+\mathrm{3}\right)}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left\{\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right)−\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}}\right)\right\} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}+....+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:−\left(\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}...+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{3}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{n}+\mathrm{3}−\mathrm{3}}{\mathrm{3}\left(\mathrm{2}{n}+\mathrm{3}\right)}\right)=\frac{{n}}{\mathrm{3}\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$

Commented by thfchristopher last updated on 23/May/22

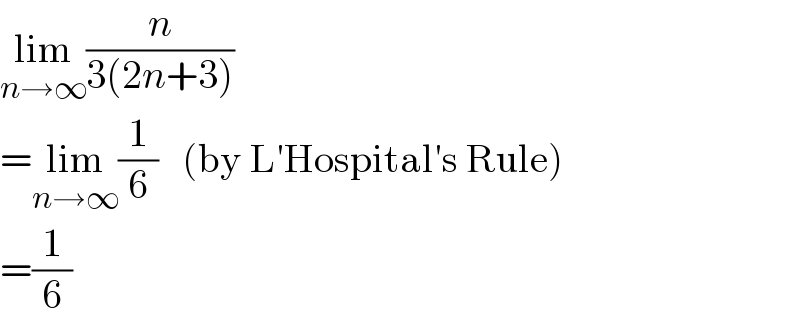
lim_(n→∞) (n/(3(2n+3))) =lim_(n→∞) (1/6) (by L′Hospital′s Rule) =(1/6)

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}}{\mathrm{3}\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{6}}\:\:\:\left(\mathrm{by}\:\mathrm{L}'\mathrm{Hospital}'\mathrm{s}\:\mathrm{Rule}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by Rasheed.Sindhi last updated on 23/May/22

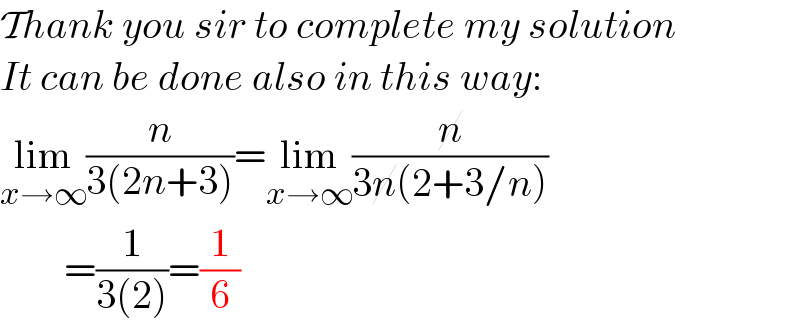
Thank you sir to complete my solution It can be done also in this way: lim_(x→∞) (n/(3(2n+3)))=lim_(x→∞) (n/(3n(2+3/n))) =(1/(3(2)))=(1/6)

$$\mathcal{T}{hank}\:{you}\:{sir}\:{to}\:{complete}\:{my}\:{solution} \\ $$$${It}\:{can}\:{be}\:{done}\:{also}\:{in}\:{this}\:{way}: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{n}}{\mathrm{3}\left(\mathrm{2}{n}+\mathrm{3}\right)}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\cancel{{n}}}{\mathrm{3}\cancel{{n}}\left(\mathrm{2}+\mathrm{3}/{n}\right)} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by Tawa11 last updated on 08/Oct/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by balirampatel last updated on 24/May/22

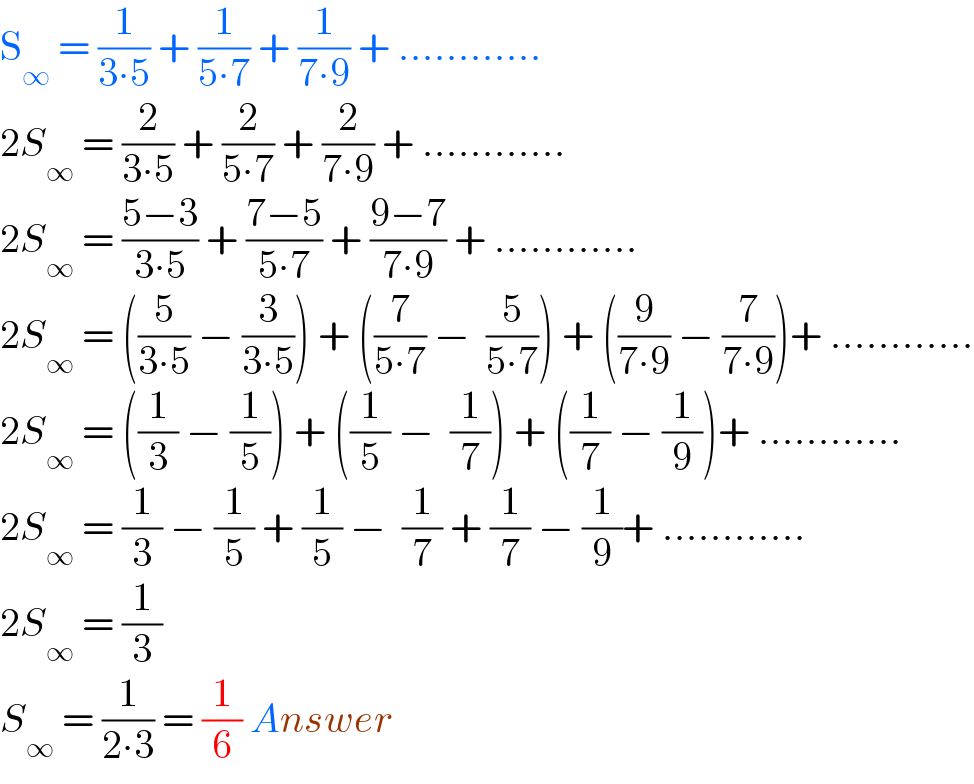
S_∞ = (1/(3∙5)) + (1/(5∙7)) + (1/(7∙9)) + ............ 2S_∞ = (2/(3∙5)) + (2/(5∙7)) + (2/(7∙9)) + ............ 2S_∞ = ((5−3)/(3∙5)) + ((7−5)/(5∙7)) + ((9−7)/(7∙9)) + ............ 2S_∞ = ((5/(3∙5)) − (3/(3∙5))) + ((7/(5∙7)) − (5/(5∙7))) + ((9/(7∙9)) − (7/(7∙9)))+ ............ 2S_∞ = ((1/3) − (1/5)) + ((1/5) − (1/7)) + ((1/7) − (1/9))+ ............ 2S_∞ = (1/3) − (1/5) + (1/5) − (1/7) + (1/7) − (1/9)+ ............ 2S_∞ = (1/3) S_∞ = (1/(2∙3)) = (1/6) Answer

$$\mathrm{S}_{\infty} \:=\:\frac{\mathrm{1}}{\mathrm{3}\centerdot\mathrm{5}}\:+\:\frac{\mathrm{1}}{\mathrm{5}\centerdot\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{7}\centerdot\mathrm{9}}\:+\:............ \\ $$$$\mathrm{2}{S}_{\infty} \:=\:\frac{\mathrm{2}}{\mathrm{3}\centerdot\mathrm{5}}\:+\:\frac{\mathrm{2}}{\mathrm{5}\centerdot\mathrm{7}}\:+\:\frac{\mathrm{2}}{\mathrm{7}\centerdot\mathrm{9}}\:+\:............ \\ $$$$\mathrm{2}{S}_{\infty} \:=\:\frac{\mathrm{5}−\mathrm{3}}{\mathrm{3}\centerdot\mathrm{5}}\:+\:\frac{\mathrm{7}−\mathrm{5}}{\mathrm{5}\centerdot\mathrm{7}}\:+\:\frac{\mathrm{9}−\mathrm{7}}{\mathrm{7}\centerdot\mathrm{9}}\:+\:............ \\ $$$$\mathrm{2}{S}_{\infty} \:=\:\left(\frac{\mathrm{5}}{\mathrm{3}\centerdot\mathrm{5}}\:−\:\frac{\mathrm{3}}{\mathrm{3}\centerdot\mathrm{5}}\right)\:+\:\left(\frac{\mathrm{7}}{\mathrm{5}\centerdot\mathrm{7}}\:−\:\:\frac{\mathrm{5}}{\mathrm{5}\centerdot\mathrm{7}}\right)\:+\:\left(\frac{\mathrm{9}}{\mathrm{7}\centerdot\mathrm{9}}\:−\:\frac{\mathrm{7}}{\mathrm{7}\centerdot\mathrm{9}}\right)+\:............ \\ $$$$\mathrm{2}{S}_{\infty} \:=\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:−\:\frac{\mathrm{1}}{\mathrm{5}}\right)\:+\:\left(\frac{\mathrm{1}}{\mathrm{5}}\:−\:\:\frac{\mathrm{1}}{\mathrm{7}}\right)\:+\:\left(\frac{\mathrm{1}}{\mathrm{7}}\:−\:\frac{\mathrm{1}}{\mathrm{9}}\right)+\:............ \\ $$$$\mathrm{2}{S}_{\infty} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\:−\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\frac{\mathrm{1}}{\mathrm{5}}\:−\:\:\frac{\mathrm{1}}{\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{7}}\:−\:\frac{\mathrm{1}}{\mathrm{9}}+\:............ \\ $$$$\mathrm{2}{S}_{\infty} \:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${S}_{\infty} \:=\:\frac{\mathrm{1}}{\mathrm{2}\centerdot\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\:{Answer} \\ $$

Commented by Rasheed.Sindhi last updated on 24/May/22

∩i⊂∈!

$$\cap\boldsymbol{\mathrm{i}}\subset\in! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com