
Question and Answers Forum
Question Number 170501 by kndramaths last updated on 25/May/22
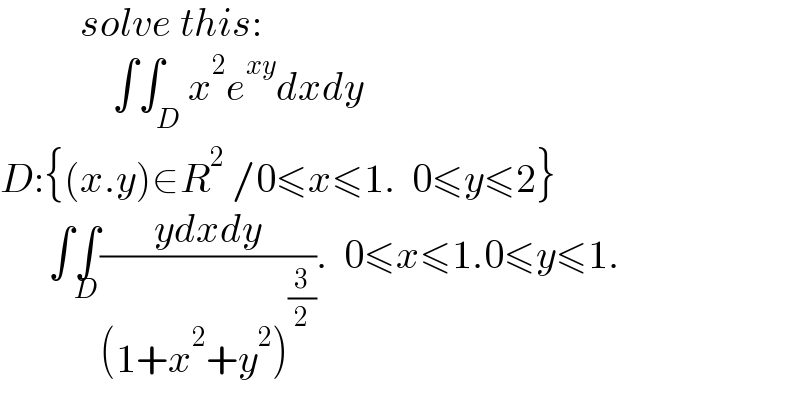
Answered by FelipeLz last updated on 26/May/22
![A = ∫∫_D x^2 e^(xy) dxdy = ∫_0 ^2 ∫_0 ^1 x^2 e^(xy) dxdy = ∫_0 ^1 [∫_0 ^2 x^2 e^(xy) dy]dx ∫_0 ^2 x^2 e^(xy) dy = x^2 ∫_0 ^2 e^(xy) dy = [x^2 (e^(xy) /x)]_(y=0) ^(y=2) = [xe^(xy) ]_(y=0) ^(y=2) = xe^(2x) −x A = ∫_0 ^1 (xe^(2x) −x)dx = ∫_0 ^1 xe^(2x) dx−∫_0 ^1 xdx = [(1/2)xe^(2x) −(1/4)e^(2x) −(x^2 /2)]_0 ^1 = (1/2)e^2 −(1/4)e^2 −(1/2)−(0−(1/4)−0) = (1/4)(e^2 −1) • B = ∫∫_D (y/((1+x^2 +y^2 )^(3/2) ))dxdy = ∫_0 ^1 [∫(y/( (√((1+x^2 +y^2 )^3 ))))dy]_(y=0) ^(y=1) dx u = 1+x^2 +y^2 ⇒ du = 2ydy ∫(y/( (√((1+x^2 +y^2 )^3 ))))dy = (1/2)∫(1/( (√u^3 )))du = −(1/( (√u))) = −(1/( (√(1+x^2 +y^2 )))) B = ∫_0 ^1 [−(1/( (√(2+x^2 ))))+(1/( (√(1+x^2 ))))]dx = ∫_0 ^1 (1/( (√(1+x^2 ))))dx−∫_0 ^1 (1/( (√(2+x^2 ))))dx = ∫_0 ^1 (1/( (√(1+x^2 ))))dx−(1/( (√2)))∫_0 ^1 (1/( (√(1+(x^2 /2)))))dx x = tan(v) ⇒ dx = sec^2 (v)dv ∫(1/( (√(1+x^2 ))))dx = ∫((sec^2 (v))/( (√(1+tan^2 (v)))))dv = ∫sec(v)dv = ln∣sec(v)+tan(v)∣ = ln∣(√(1+x^2 ))+x∣ = sinh^(−1) (x) (x/( (√2))) = tan(t) ⇒ dx = (√2)sec^2 (t)dt (1/( (√2)))∫(1/( (√(1+(x^2 /2)))))dx = ∫((sec^2 (t))/( (√(1+tan^2 (t)))))dt = ln∣sec(t)+tan(t)∣ = ln∣(√(1+(x^2 /2)))+(x/( (√2)))∣ = sinh^(−1) ((x/( (√2)))) B = [sinh^(−1) (x)]_0 ^1 −[sinh^(−1) ((x/( (√2))))]_0 ^1 = sinh^(−1) (1)−sinh^(−1) ((1/( (√2)))) = ln((√2)+1)−ln(((1+(√3))/( (√2)))) = ln(((2+(√2))/(1+(√3))))](Q170526.png)
| ||
Question and Answers Forum | ||
Question Number 170501 by kndramaths last updated on 25/May/22 | ||
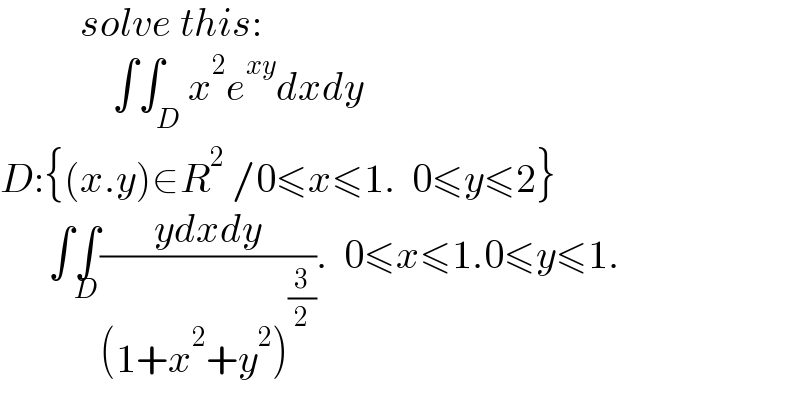 | ||
Answered by FelipeLz last updated on 26/May/22 | ||
![A = ∫∫_D x^2 e^(xy) dxdy = ∫_0 ^2 ∫_0 ^1 x^2 e^(xy) dxdy = ∫_0 ^1 [∫_0 ^2 x^2 e^(xy) dy]dx ∫_0 ^2 x^2 e^(xy) dy = x^2 ∫_0 ^2 e^(xy) dy = [x^2 (e^(xy) /x)]_(y=0) ^(y=2) = [xe^(xy) ]_(y=0) ^(y=2) = xe^(2x) −x A = ∫_0 ^1 (xe^(2x) −x)dx = ∫_0 ^1 xe^(2x) dx−∫_0 ^1 xdx = [(1/2)xe^(2x) −(1/4)e^(2x) −(x^2 /2)]_0 ^1 = (1/2)e^2 −(1/4)e^2 −(1/2)−(0−(1/4)−0) = (1/4)(e^2 −1) • B = ∫∫_D (y/((1+x^2 +y^2 )^(3/2) ))dxdy = ∫_0 ^1 [∫(y/( (√((1+x^2 +y^2 )^3 ))))dy]_(y=0) ^(y=1) dx u = 1+x^2 +y^2 ⇒ du = 2ydy ∫(y/( (√((1+x^2 +y^2 )^3 ))))dy = (1/2)∫(1/( (√u^3 )))du = −(1/( (√u))) = −(1/( (√(1+x^2 +y^2 )))) B = ∫_0 ^1 [−(1/( (√(2+x^2 ))))+(1/( (√(1+x^2 ))))]dx = ∫_0 ^1 (1/( (√(1+x^2 ))))dx−∫_0 ^1 (1/( (√(2+x^2 ))))dx = ∫_0 ^1 (1/( (√(1+x^2 ))))dx−(1/( (√2)))∫_0 ^1 (1/( (√(1+(x^2 /2)))))dx x = tan(v) ⇒ dx = sec^2 (v)dv ∫(1/( (√(1+x^2 ))))dx = ∫((sec^2 (v))/( (√(1+tan^2 (v)))))dv = ∫sec(v)dv = ln∣sec(v)+tan(v)∣ = ln∣(√(1+x^2 ))+x∣ = sinh^(−1) (x) (x/( (√2))) = tan(t) ⇒ dx = (√2)sec^2 (t)dt (1/( (√2)))∫(1/( (√(1+(x^2 /2)))))dx = ∫((sec^2 (t))/( (√(1+tan^2 (t)))))dt = ln∣sec(t)+tan(t)∣ = ln∣(√(1+(x^2 /2)))+(x/( (√2)))∣ = sinh^(−1) ((x/( (√2)))) B = [sinh^(−1) (x)]_0 ^1 −[sinh^(−1) ((x/( (√2))))]_0 ^1 = sinh^(−1) (1)−sinh^(−1) ((1/( (√2)))) = ln((√2)+1)−ln(((1+(√3))/( (√2)))) = ln(((2+(√2))/(1+(√3))))](Q170526.png) | ||
| ||