
Question and Answers Forum
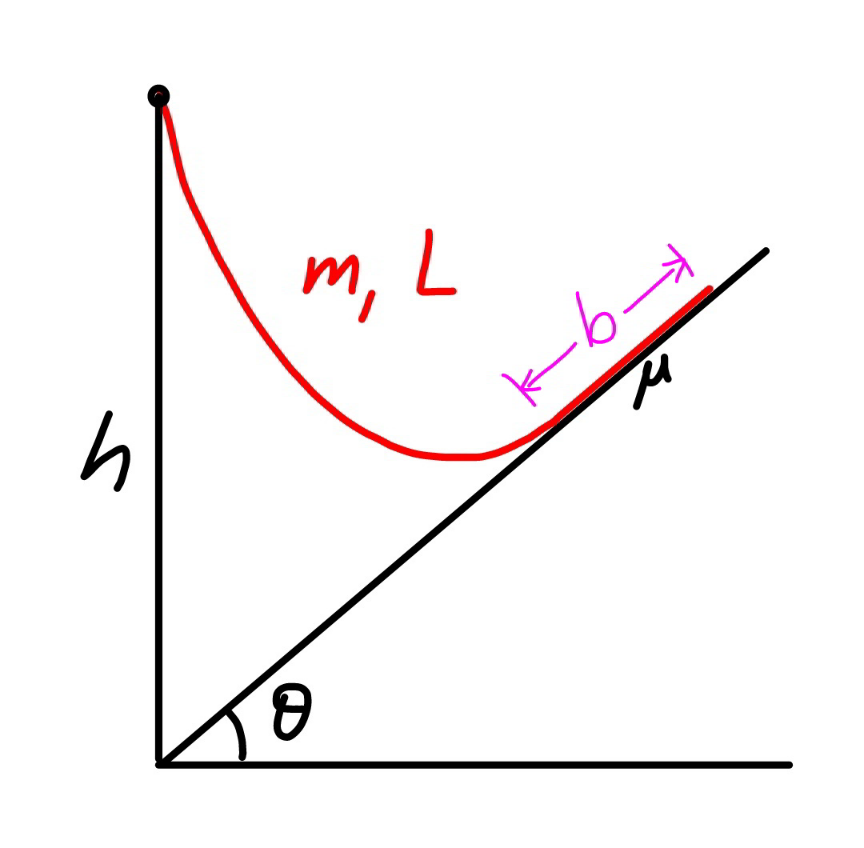
Question Number 170601 by mr W last updated on 27/May/22
Commented by mr W last updated on 29/May/22

Answered by aleks041103 last updated on 28/May/22
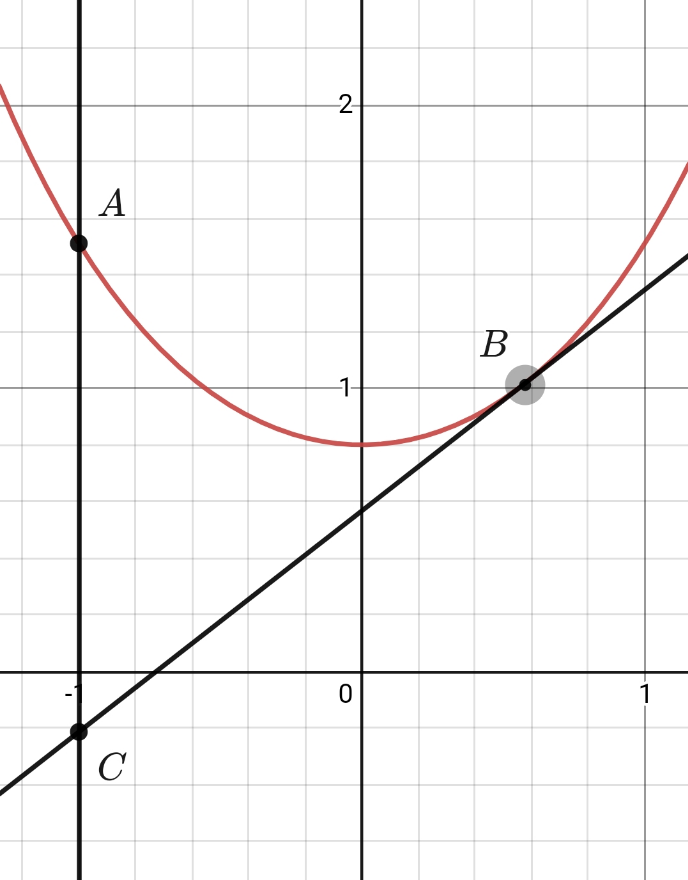
Commented by aleks041103 last updated on 28/May/22
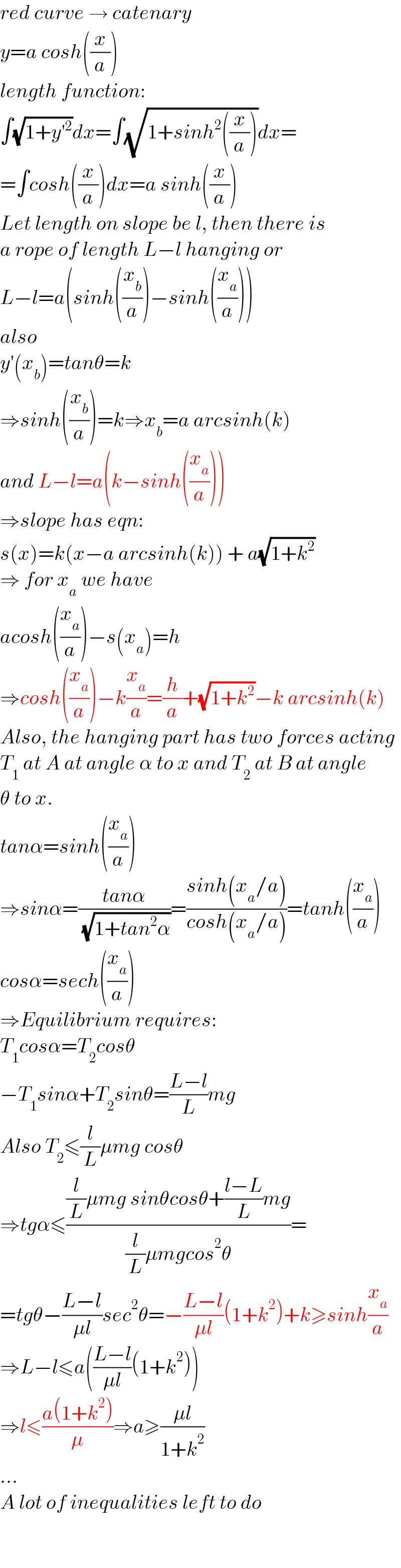
Commented by mr W last updated on 29/May/22
Answered by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22

Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
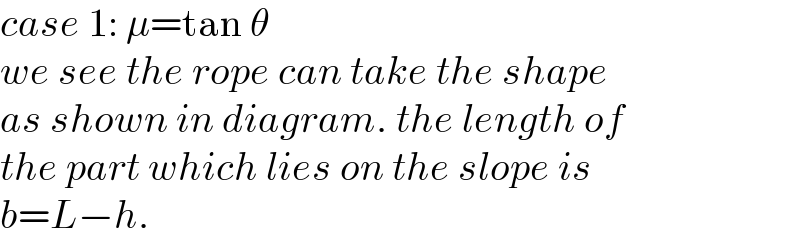
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22

Commented by mr W last updated on 29/May/22
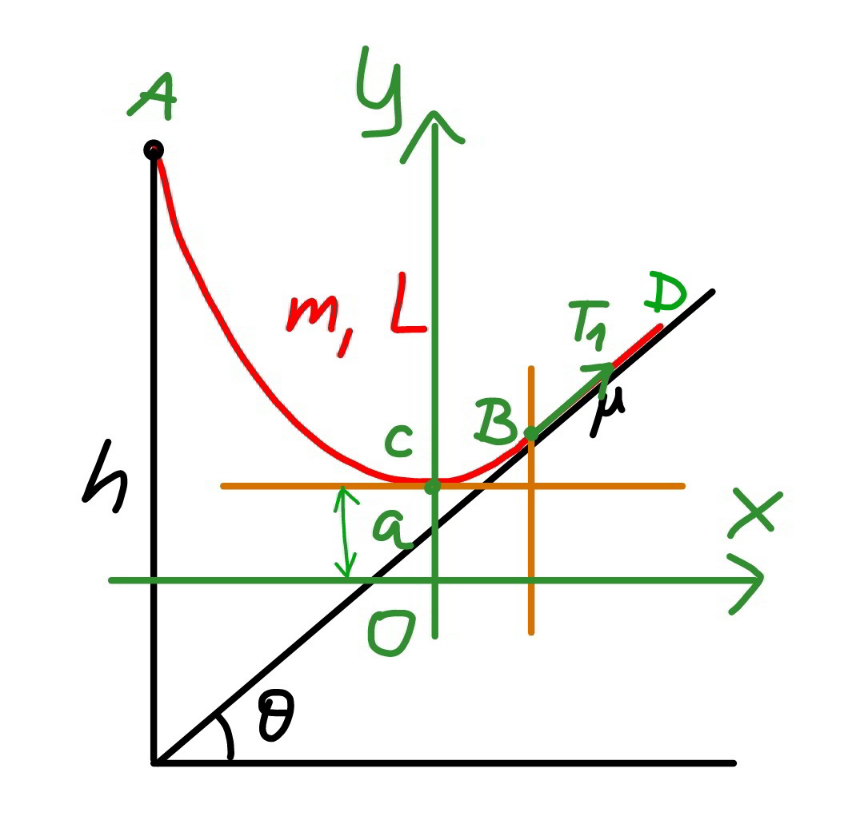
Commented by mr W last updated on 29/May/22
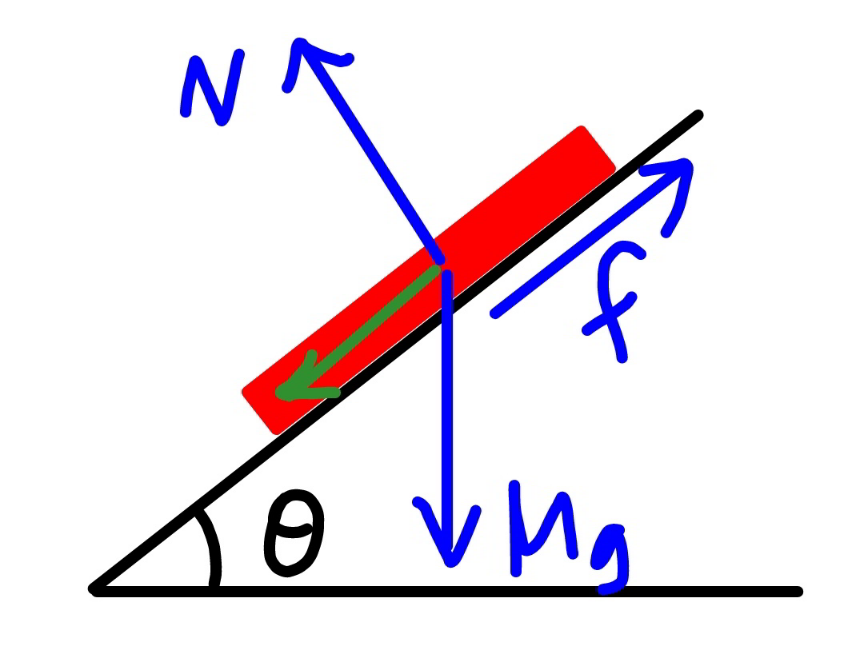
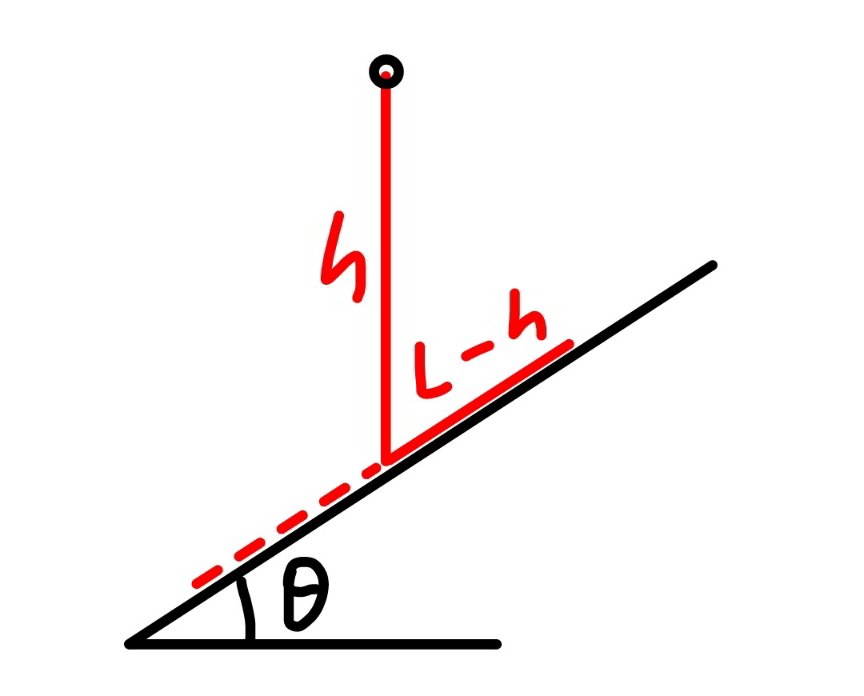
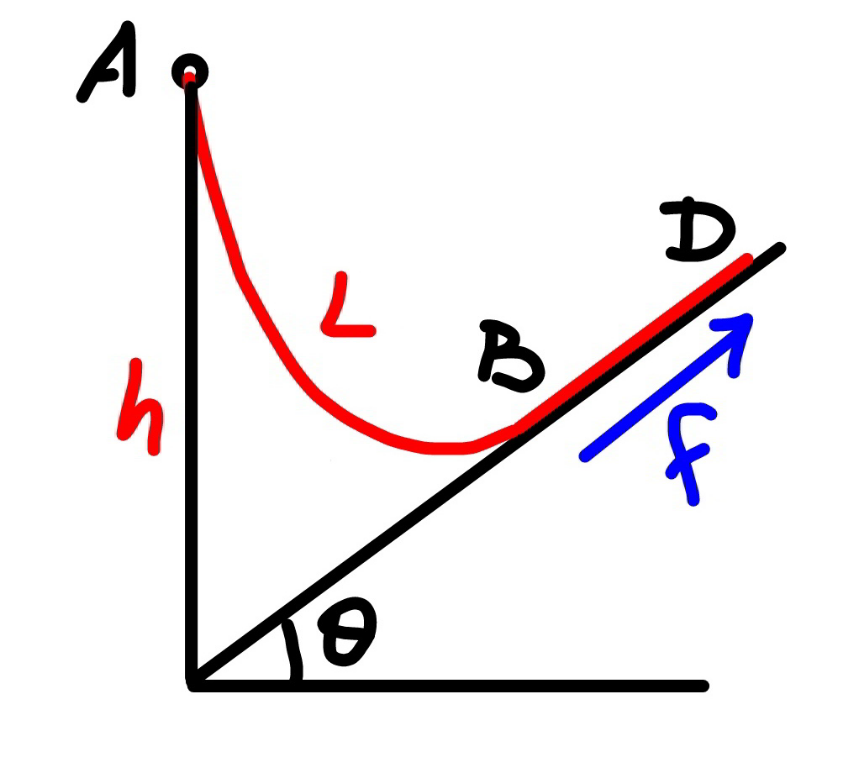
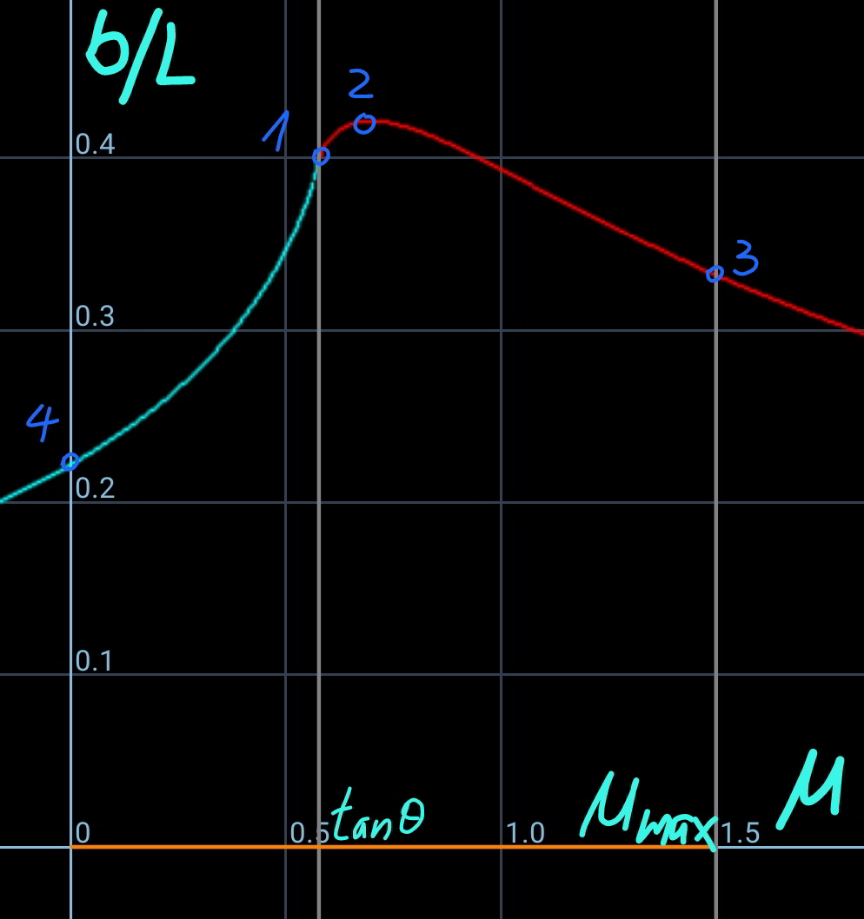
![say the length of the rope part which lies on the inclined plane is b. ρ=(m/L) the friction force between rope and the slope is f. f=μρgb cos θ with tan θ<μ≤μ_(max) tension in the rope at point B: T_1 =f−ρgb sin θ=(μ cos θ−sin θ)ρgb let μ′=μ cos θ−sin θ T_1 =μ′ρgb T_0 =T_1 cos θ=μ′ρgb cos θ define a=(T_0 /(ρg))=μ′b cos θ the hanging rope from point A to B is part of a catenary. w.r.t. the coordinate system as shown, y=a cosh (x/a) y′=sinh (x/a) s=a sinh (x/a) tan θ=sinh (x_B /a) ⇒(x_B /a)=sinh^(−1) (tan θ) s_1 =CB^(⌢) =a sinh (x_B /a)=a tan θ AC^(⌢) =L−b−s_1 =a sinh (x_A /a) L−b−a tan θ=a sinh (x_A /a) ⇒(x_A /a)=sinh^(−1) (((L−b)/a)−tan θ) y_A −y_B =h−(x_A +x_B ) tan θ a cosh (x_A /a)−a cosh (x_B /a)=h−(x_A +x_B ) tan θ cosh (x_A /a)−cosh (x_B /a)=(h/a)−((x_A /a)+(x_B /a)) tan θ cosh [sinh^(−1) (((L−b)/a)−tan θ)]−cosh [sinh^(−1) (tan θ)]=(h/a)−[sinh^(−1) (((L−b)/a)−tan θ)+sinh^(−1) (tan θ)] tan θ let (b/L)=(1/λ) cosh [sinh^(−1) (((λ−1)/(μ′ cos θ))−tan θ)]−cosh [sinh^(−1) (tan θ)]=((λh)/(μ′L cos θ))−[sinh^(−1) (((λ−1)/(μ′ cos θ))−tan θ)+sinh^(−1) (tan θ)] tan θ ⇒[sinh^(−1) (((𝛌−1)/(𝛍′ cos 𝛉))−tan 𝛉)+sinh^(−1) (tan 𝛉)]sin 𝛉=1+((𝛌h)/(𝛍′L))−(√(1+(((𝛌−1)/(𝛍′)))^2 −2(((𝛌−1)/(𝛍′))) sin 𝛉)) this equation shows the relationship between λ and the actual friction coefficient μ (tan θ<μ≤μ_(max) ). generally this relationship looks like as shown in the diagram below. example: h=3m, L=5m, θ=30°, μ_(max) =1.5 ⇒(b_(min) /L)=0.33202 at μ=1.5 ⇒(b_(max) /L)=0.43165 at μ=0.7](Q170693.png)
Commented by mr W last updated on 29/May/22
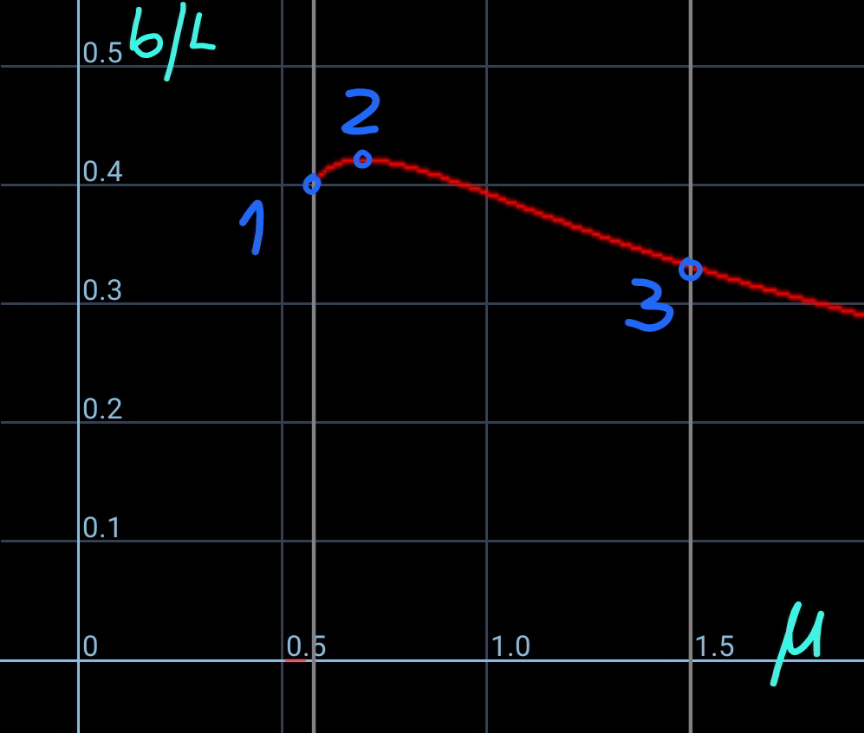
Commented by mr W last updated on 29/May/22

Commented by mr W last updated on 29/May/22
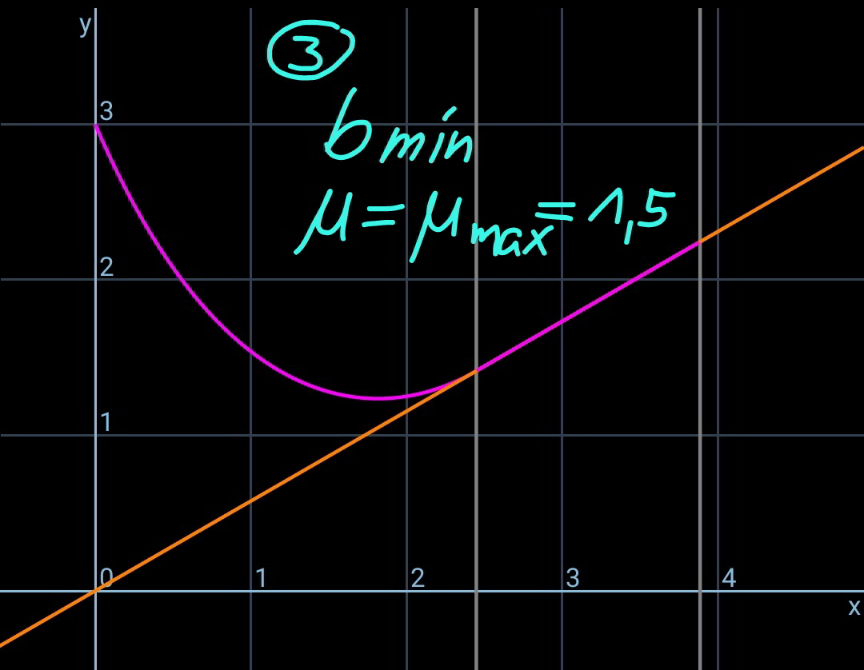
Commented by mr W last updated on 29/May/22
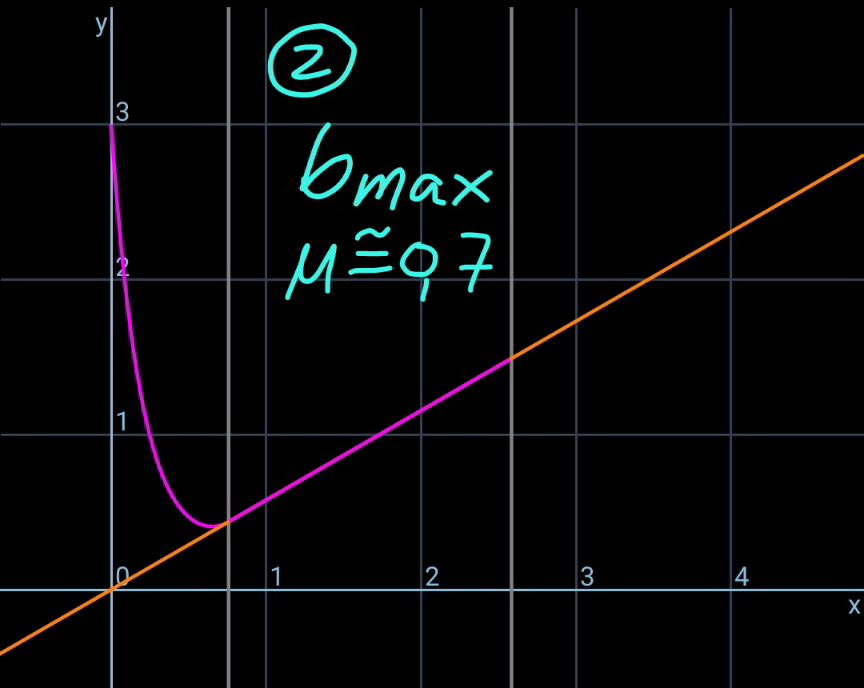
Commented by mr W last updated on 29/May/22
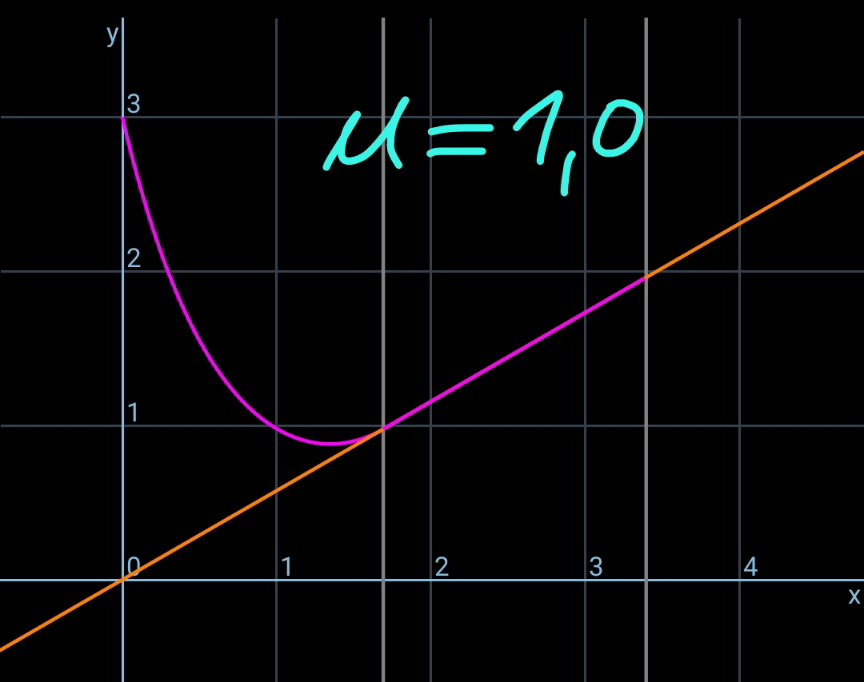
Commented by mr W last updated on 29/May/22
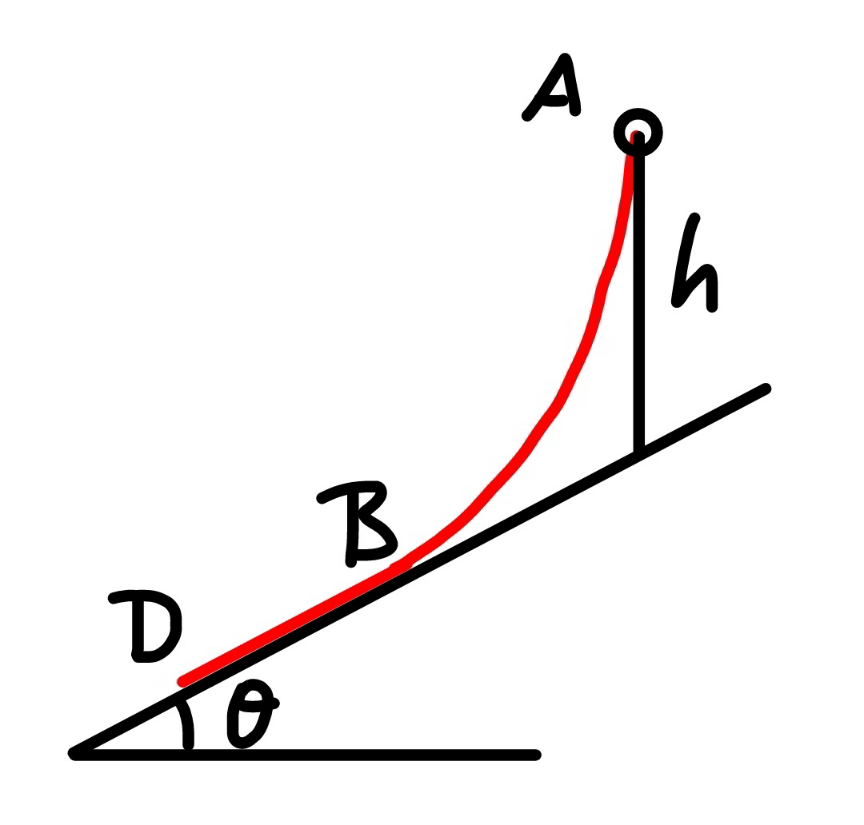
Commented by mr W last updated on 29/May/22
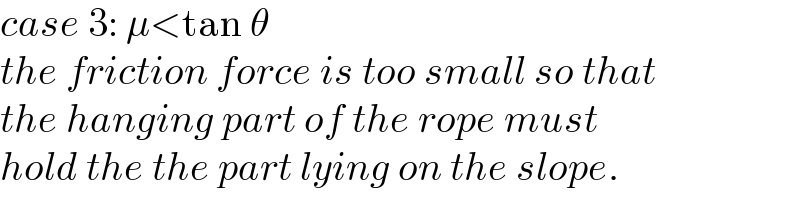
Commented by mr W last updated on 29/May/22
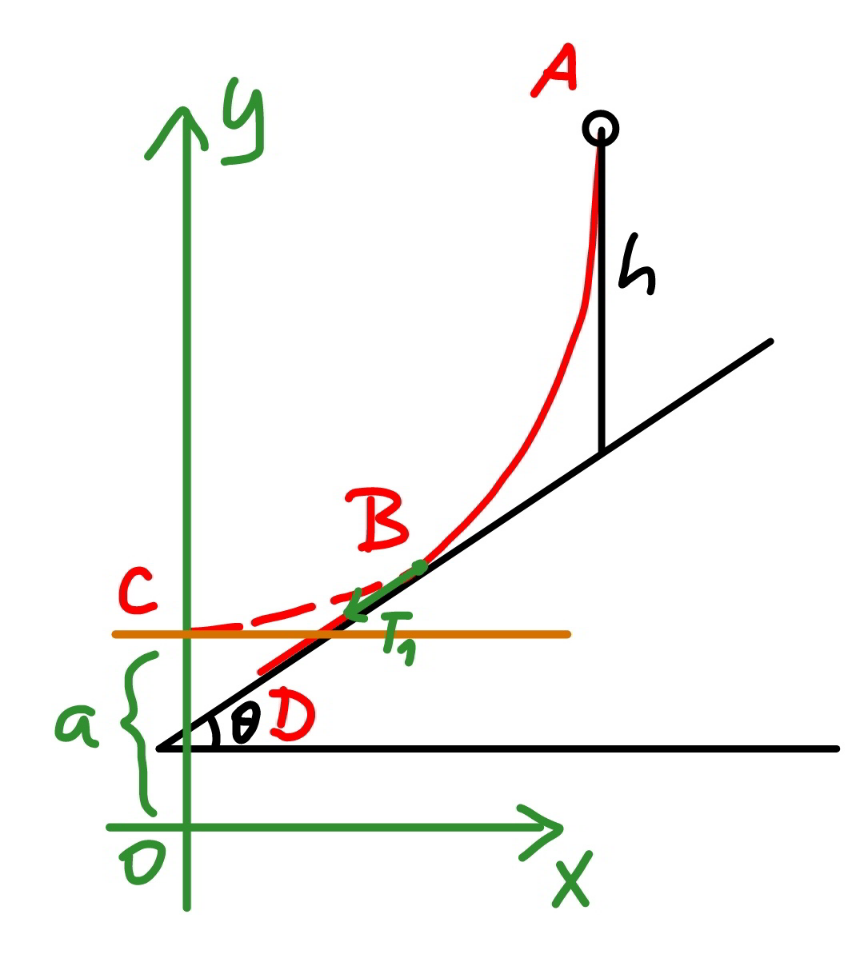
Commented by mr W last updated on 29/May/22
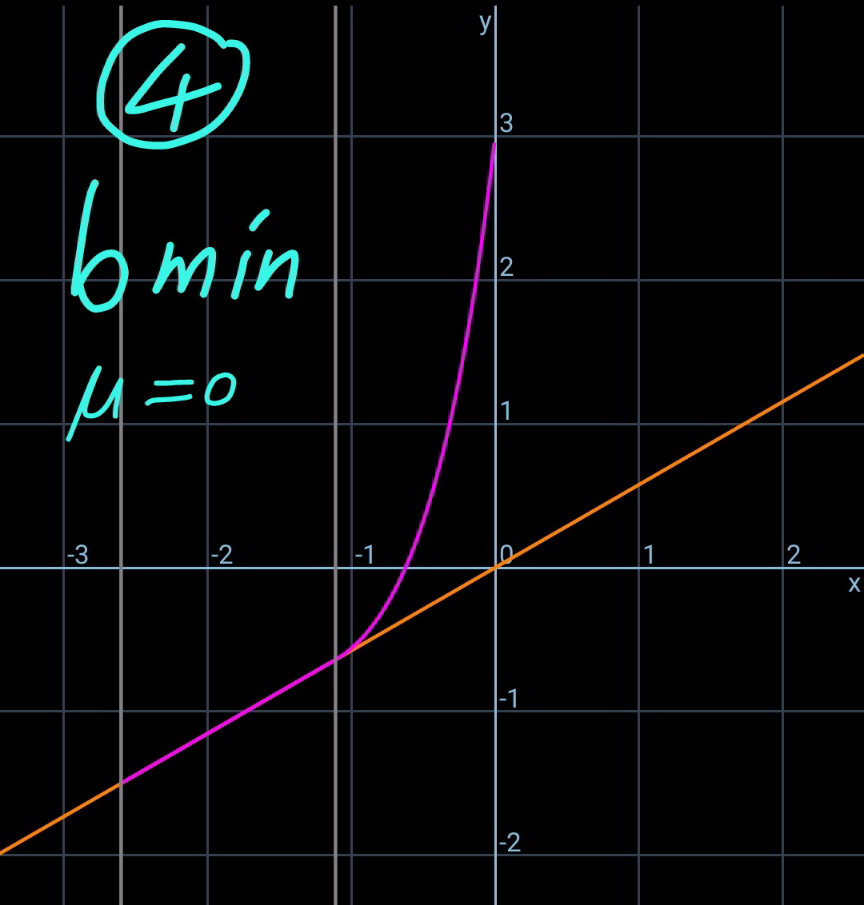
Commented by mr W last updated on 29/May/22
![say the length of the rope part which lies on the inclined plane is b. the friction force between rope and the slope is f. f=μρgb cos θ with 0≤μ<tan θ tension in the rope at point B: T_1 =ρgb sin θ−f=(sin θ−μ cos θ)ρgb let μ′=μ cos θ−sin θ T_1 =−μ′ρgb T_0 =T_1 cos θ=−μ′ρgb cos θ define a=(T_0 /(ρg))=−μ′b cos θ the hanging rope from point A to B is part of a catenary. w.r.t. the coordinate system as shown, y=a cosh (x/a) y′=sinh (x/a) s=a sinh (x/a) tan θ=sinh (x_B /a) ⇒(x_B /a)=sinh^(−1) (tan θ) s_1 =CB^(⌢) =a sinh (x_B /a)=a tan θ AC^(⌢) =L−b+s_1 =a sinh (x_A /a) L−b+a tan θ=a sinh (x_A /a) ⇒(x_A /a)=sinh^(−1) (((L−b)/a)+tan θ) y_A −y_B =h+(x_A −x_B ) tan θ a cosh (x_A /a)−a cosh (x_B /a)=h+(x_A −x_B ) tan θ cosh (x_A /a)−cosh (x_B /a)=(h/a)+((x_A /a)−(x_B /a)) tan θ cosh [sinh^(−1) (((L−b)/a)+tan θ)]−cosh [sinh^(−1) (tan θ)]=(h/a)+[sinh^(−1) (((L−b)/a)+tan θ)−sinh^(−1) (tan θ)] tan θ let (b/L)=(1/λ) cosh [sinh^(−1) (−((λ−1)/(μ′ cos θ))+tan θ)]−cosh [sinh^(−1) (tan θ)]=−((λh)/(μ′L cos θ))+[sinh^(−1) (−((λ−1)/(μ′ cos θ))+tan θ)−sinh^(−1) (tan θ)] tan θ ⇒[sinh^(−1) (((𝛌−1)/(𝛍′ cos 𝛉))−tan 𝛉)+sinh^(−1) (tan 𝛉)]sin 𝛉=1− ((𝛌h)/(𝛍′))−(√(1+(((𝛌−1)/(𝛍′)))^2 −2(((𝛌−1)/(𝛍′)))sin 𝛉)) this equation shows the relationship between λ and the actual friction coefficient μ (0≤μ<tan θ). generally this relationship looks like as shown in the diagram below. example: h=3m, L=5m, θ=30°, μ_(max) =1.5 ⇒(b_(min) /L)=0.22196 at μ=0 (point 4) ⇒(b_(max) /L)=0.43165 at μ=0.7 (point 2)](Q170717.png)
Commented by mr W last updated on 30/May/22
Commented by Tawa11 last updated on 06/Oct/22

