Question and Answers Forum
Question Number 170738 by Tawa11 last updated on 30/May/22
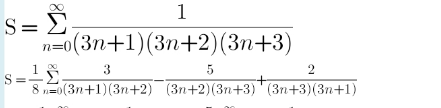
Commented by Tawa11 last updated on 30/May/22
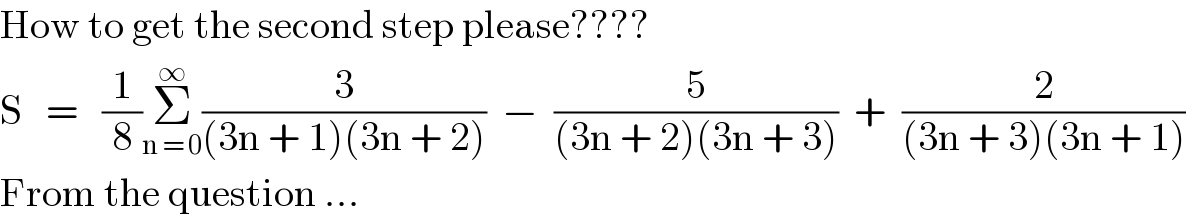
Commented by mr W last updated on 30/May/22
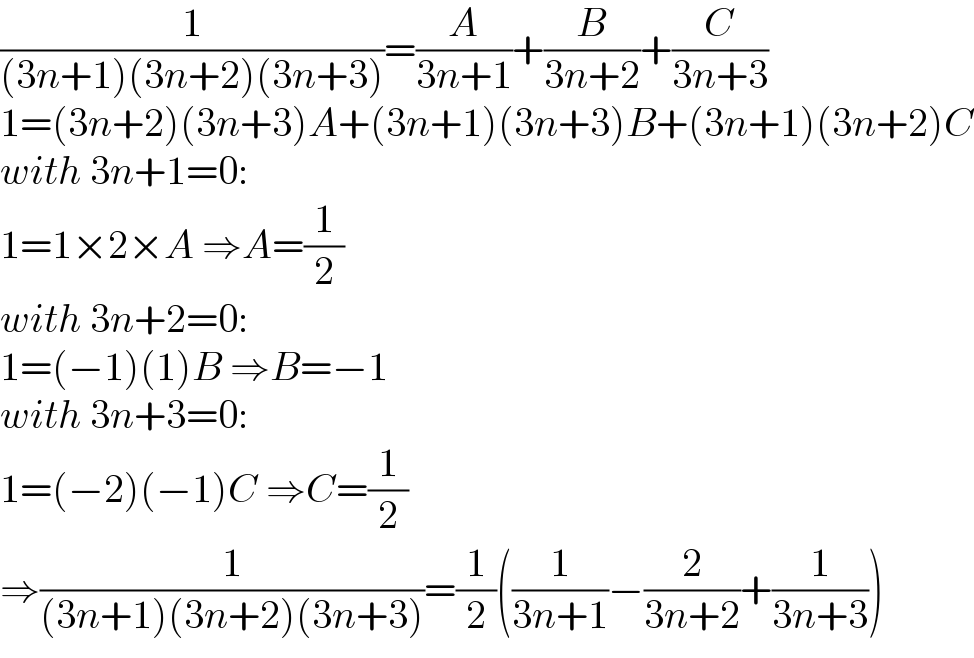
Commented by Tawa11 last updated on 30/May/22
Commented by Tawa11 last updated on 30/May/22
Commented by Tawa11 last updated on 30/May/22
Commented by Tawa11 last updated on 30/May/22
Commented by Tawa11 last updated on 30/May/22

Commented by mr W last updated on 30/May/22
![(1/((3n+1)(3n+2)(3n+3)))=(A/((3n+1)(3n+2)))+(B/((3n+2)(3n+3)))+(C/((3n+3)(3n+1))) (1/((3n+1)(3n+2)(3n+3)))=((3n(A+B+C)+(3A+B+2C))/((3n+1)(3n+2)(3n+1))) ⇒A+B+C=0 ⇒3A+B+2C=1 ⇒2A+2B+2C+A−B=1 ⇒A−B=1 you may find infinite possibilities for A,B,C. for example as the step 2 in the solution did: A=(3/8), B=−(5/8), C=(2/8) A+B+C=((3−5+2)/8)=0 ✓ 3A+B+2C=((3×3−5+2×2)/8)=1 ✓ but this was arbitrarily done. so you don′t need to request yourself to get the same. certainly you can also take other values for A,B,C, because as i said there are infinite solutions. but you don′t need to take any special values for A,B,C in order to solve the problem. Σ_(n=0) ^∞ (1/((3n+1)(3n+2)(3n+3))) =Σ_(n=0) ^∞ [(A/((3n+1)(3n+2)))+(B/((3n+2)(3n+3)))+(C/((3n+3)(3n+1)))] =(1/9)Σ_(n=0) ^∞ [(A/((n+(1/3))(n+(2/3))))+(B/((n+(2/3))(n+1)))+(C/((n+1)(n+(1/3))))] =(1/9){((A[ψ((2/3))−ψ((1/3))])/((2/3)−(1/3)))+((B[ψ(1)−ψ((2/3))])/(1−(2/3)))+((C[ψ(1)−ψ((1/3))])/(1−(1/3)))} =(1/3){((A[ψ((2/3))−ψ((1/3))])/1)+((B[ψ(1)−ψ((2/3))])/1)+((C[ψ(1)−ψ((1/3))])/2)} =(1/6){2A[ψ((2/3))−ψ((1/3))]+2B[ψ(1)−ψ((2/3))]+C[ψ(1)−ψ((1/3))]} =(1/6){2Aψ((2/3))−2Aψ((1/3))+2Bψ(1)−2Bψ((2/3))+Cψ(1)−Cψ((1/3))} =(2/3){(2A−2B)ψ((2/3))−(2A+C)ψ((1/3))+(2B+C)ψ(1)} =(1/6){(2A−2B)(ψ((1/3))+(π/( (√3))))−(2A+C)ψ((1/3))+(2B+C)ψ(1)} =(1/6){2(A−B)(π/( (√3)))+(2B+C)(ψ(1)−ψ((1/3)))} =(1/6){2(A−B)(π/( (√3)))+(2B+C)((π/(2(√3)))+(3/2)ln 3)} =(((A−B))/4)((π/( (√3)))−ln 3) =(1/4)((π/( (√3)))−ln 3) ✓](Q170782.png)
Commented by Tawa11 last updated on 30/May/22