
Question and Answers Forum
Question Number 170802 by Sotoberry last updated on 31/May/22

Answered by thfchristopher last updated on 31/May/22
![∫ln (x+x^2 )dx =∫ln x(x+1)dx =∫ln xdx+∫ln (x+1)dx =xln x−∫xd(ln x)+xln (x+1)−∫xd[ln (x+1)] =xln x−∫dx+xln (x+1)−∫(x/(x+1))dx =xln x−x+xln (x+1)−∫(1−(1/(x+1)))dx =xln x−x+xln (x+1)−∫dx+∫(1/(x+1))dx =xln x−2x+(x+1)ln (x+1)+C =ln x^x (x+1)^(x+1) −2x+C](Q170804.png)
Answered by Mathspace last updated on 31/May/22
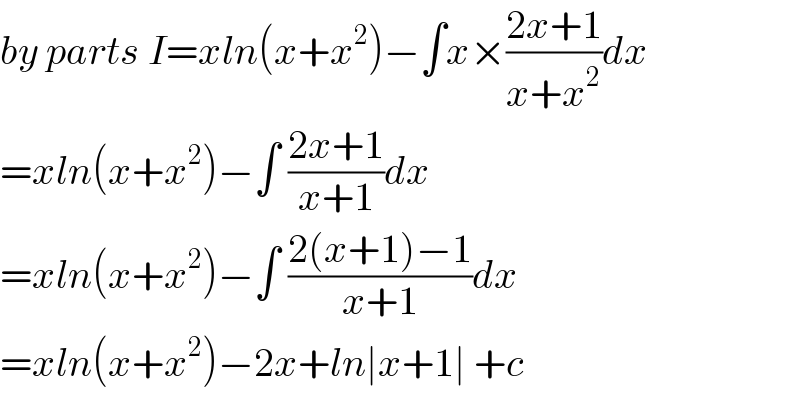
| ||
Question and Answers Forum | ||
Question Number 170802 by Sotoberry last updated on 31/May/22 | ||
 | ||
Answered by thfchristopher last updated on 31/May/22 | ||
![∫ln (x+x^2 )dx =∫ln x(x+1)dx =∫ln xdx+∫ln (x+1)dx =xln x−∫xd(ln x)+xln (x+1)−∫xd[ln (x+1)] =xln x−∫dx+xln (x+1)−∫(x/(x+1))dx =xln x−x+xln (x+1)−∫(1−(1/(x+1)))dx =xln x−x+xln (x+1)−∫dx+∫(1/(x+1))dx =xln x−2x+(x+1)ln (x+1)+C =ln x^x (x+1)^(x+1) −2x+C](Q170804.png) | ||
| ||
Answered by Mathspace last updated on 31/May/22 | ||
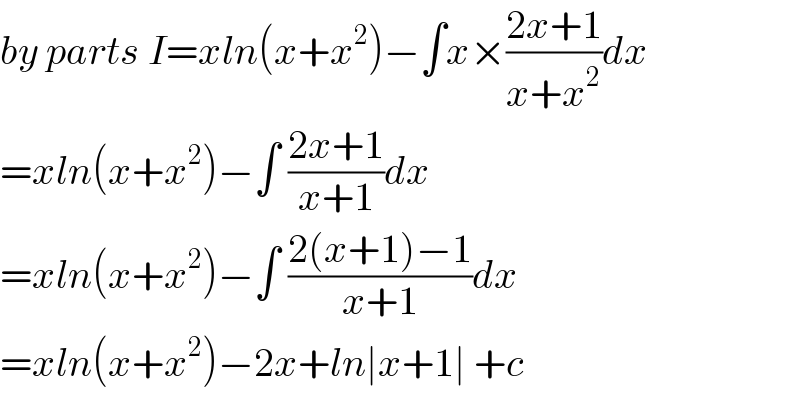 | ||
| ||