Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 170890 by nadovic last updated on 02/Jun/22

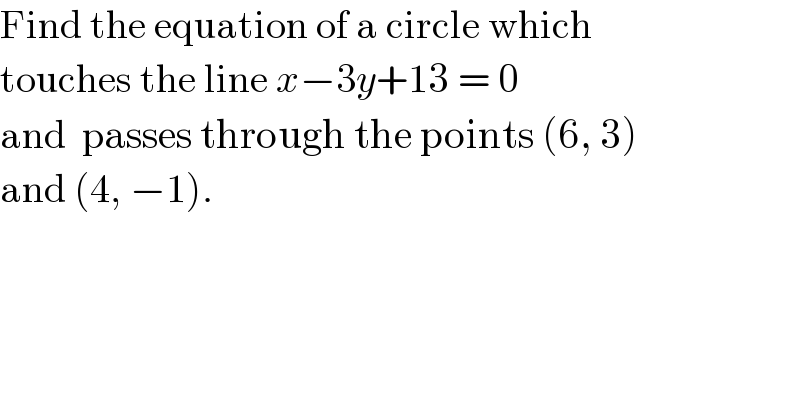
Find the equation of a circle which touches the line x−3y+13 = 0 and passes through the points (6, 3) and (4, −1).

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{which} \\ $$$$\mathrm{touches}\:\mathrm{the}\:\mathrm{line}\:{x}−\mathrm{3}{y}+\mathrm{13}\:=\:\mathrm{0}\: \\ $$$$\mathrm{and}\:\:\mathrm{passes}\:\mathrm{through}\:\mathrm{the}\:\mathrm{points}\:\left(\mathrm{6},\:\mathrm{3}\right) \\ $$$$\mathrm{and}\:\left(\mathrm{4},\:−\mathrm{1}\right). \\ $$

Answered by aleks041103 last updated on 02/Jun/22

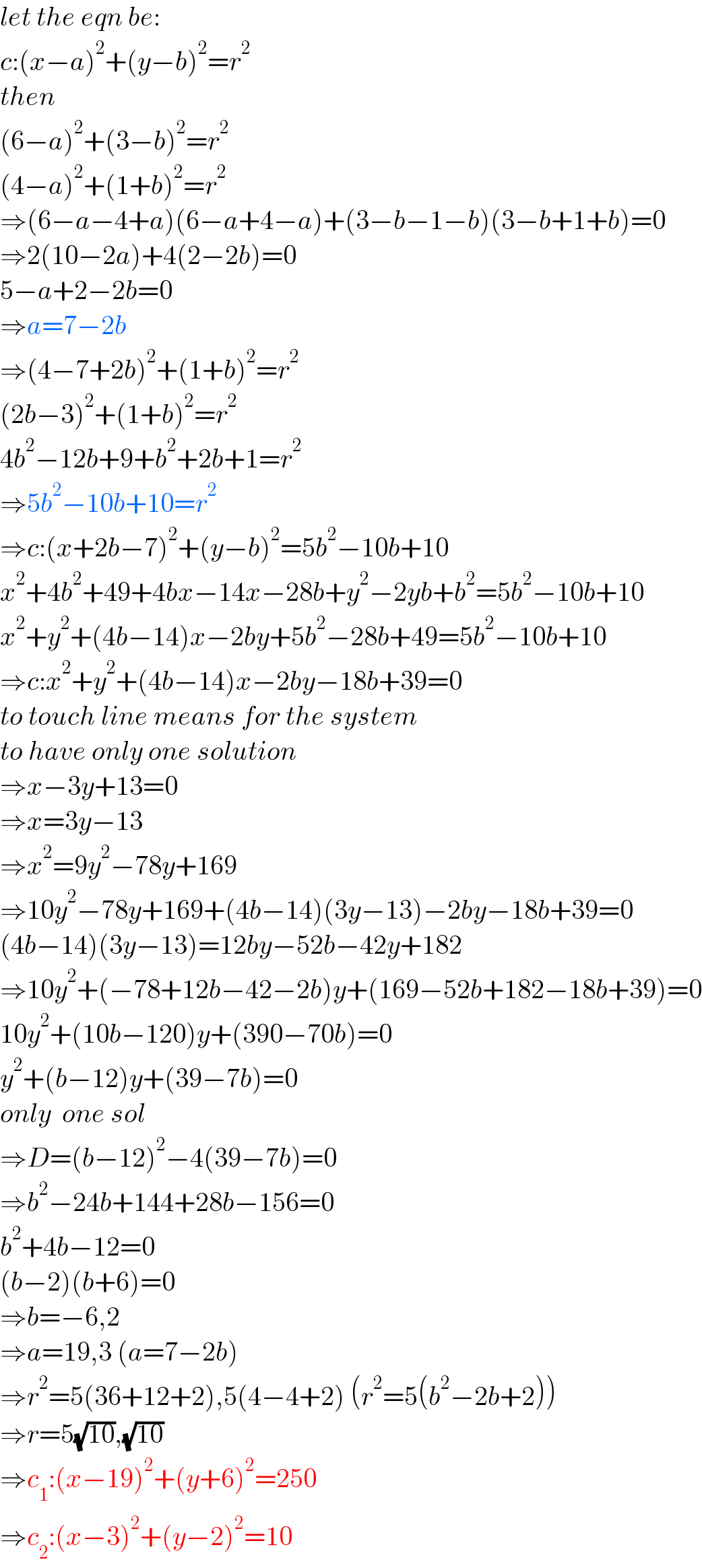
let the eqn be: c:(x−a)^2 +(y−b)^2 =r^2 then (6−a)^2 +(3−b)^2 =r^2 (4−a)^2 +(1+b)^2 =r^2 ⇒(6−a−4+a)(6−a+4−a)+(3−b−1−b)(3−b+1+b)=0 ⇒2(10−2a)+4(2−2b)=0 5−a+2−2b=0 ⇒a=7−2b ⇒(4−7+2b)^2 +(1+b)^2 =r^2 (2b−3)^2 +(1+b)^2 =r^2 4b^2 −12b+9+b^2 +2b+1=r^2 ⇒5b^2 −10b+10=r^2 ⇒c:(x+2b−7)^2 +(y−b)^2 =5b^2 −10b+10 x^2 +4b^2 +49+4bx−14x−28b+y^2 −2yb+b^2 =5b^2 −10b+10 x^2 +y^2 +(4b−14)x−2by+5b^2 −28b+49=5b^2 −10b+10 ⇒c:x^2 +y^2 +(4b−14)x−2by−18b+39=0 to touch line means for the system to have only one solution ⇒x−3y+13=0 ⇒x=3y−13 ⇒x^2 =9y^2 −78y+169 ⇒10y^2 −78y+169+(4b−14)(3y−13)−2by−18b+39=0 (4b−14)(3y−13)=12by−52b−42y+182 ⇒10y^2 +(−78+12b−42−2b)y+(169−52b+182−18b+39)=0 10y^2 +(10b−120)y+(390−70b)=0 y^2 +(b−12)y+(39−7b)=0 only one sol ⇒D=(b−12)^2 −4(39−7b)=0 ⇒b^2 −24b+144+28b−156=0 b^2 +4b−12=0 (b−2)(b+6)=0 ⇒b=−6,2 ⇒a=19,3 (a=7−2b) ⇒r^2 =5(36+12+2),5(4−4+2) (r^2 =5(b^2 −2b+2)) ⇒r=5(√(10)),(√(10)) ⇒c_1 :(x−19)^2 +(y+6)^2 =250 ⇒c_2 :(x−3)^2 +(y−2)^2 =10

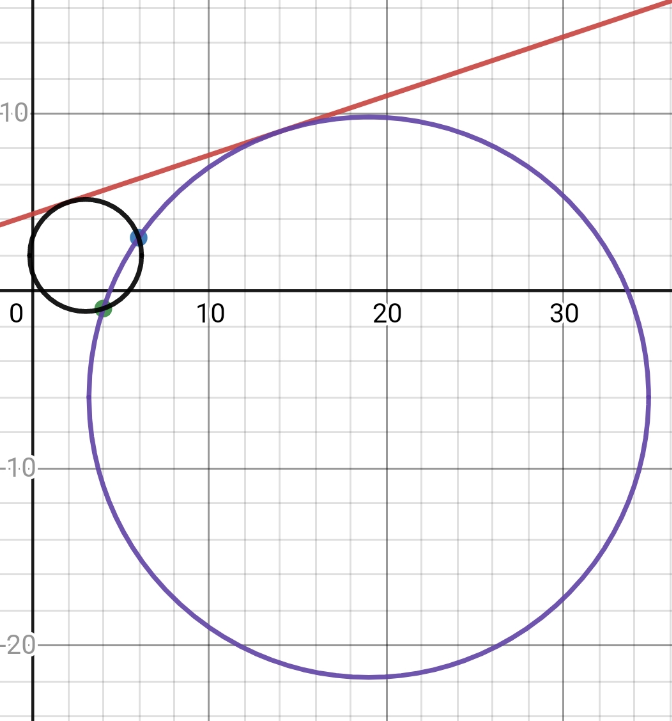
$${let}\:{the}\:{eqn}\:{be}: \\ $$$${c}:\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${then} \\ $$$$\left(\mathrm{6}−{a}\right)^{\mathrm{2}} +\left(\mathrm{3}−{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{4}−{a}\right)^{\mathrm{2}} +\left(\mathrm{1}+{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{6}−{a}−\mathrm{4}+{a}\right)\left(\mathrm{6}−{a}+\mathrm{4}−{a}\right)+\left(\mathrm{3}−{b}−\mathrm{1}−{b}\right)\left(\mathrm{3}−{b}+\mathrm{1}+{b}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{10}−\mathrm{2}{a}\right)+\mathrm{4}\left(\mathrm{2}−\mathrm{2}{b}\right)=\mathrm{0} \\ $$$$\mathrm{5}−{a}+\mathrm{2}−\mathrm{2}{b}=\mathrm{0} \\ $$$$\Rightarrow{a}=\mathrm{7}−\mathrm{2}{b} \\ $$$$\Rightarrow\left(\mathrm{4}−\mathrm{7}+\mathrm{2}{b}\right)^{\mathrm{2}} +\left(\mathrm{1}+{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}{b}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{1}+{b}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{4}{b}^{\mathrm{2}} −\mathrm{12}{b}+\mathrm{9}+{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}={r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{5}{b}^{\mathrm{2}} −\mathrm{10}{b}+\mathrm{10}={r}^{\mathrm{2}} \\ $$$$\Rightarrow{c}:\left({x}+\mathrm{2}{b}−\mathrm{7}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} =\mathrm{5}{b}^{\mathrm{2}} −\mathrm{10}{b}+\mathrm{10} \\ $$$${x}^{\mathrm{2}} +\mathrm{4}{b}^{\mathrm{2}} +\mathrm{49}+\mathrm{4}{bx}−\mathrm{14}{x}−\mathrm{28}{b}+{y}^{\mathrm{2}} −\mathrm{2}{yb}+{b}^{\mathrm{2}} =\mathrm{5}{b}^{\mathrm{2}} −\mathrm{10}{b}+\mathrm{10} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left(\mathrm{4}{b}−\mathrm{14}\right){x}−\mathrm{2}{by}+\mathrm{5}{b}^{\mathrm{2}} −\mathrm{28}{b}+\mathrm{49}=\mathrm{5}{b}^{\mathrm{2}} −\mathrm{10}{b}+\mathrm{10} \\ $$$$\Rightarrow{c}:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\left(\mathrm{4}{b}−\mathrm{14}\right){x}−\mathrm{2}{by}−\mathrm{18}{b}+\mathrm{39}=\mathrm{0} \\ $$$${to}\:{touch}\:{line}\:{means}\:{for}\:{the}\:{system} \\ $$$${to}\:{have}\:{only}\:{one}\:{solution} \\ $$$$\Rightarrow{x}−\mathrm{3}{y}+\mathrm{13}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{3}{y}−\mathrm{13} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{9}{y}^{\mathrm{2}} −\mathrm{78}{y}+\mathrm{169} \\ $$$$\Rightarrow\mathrm{10}{y}^{\mathrm{2}} −\mathrm{78}{y}+\mathrm{169}+\left(\mathrm{4}{b}−\mathrm{14}\right)\left(\mathrm{3}{y}−\mathrm{13}\right)−\mathrm{2}{by}−\mathrm{18}{b}+\mathrm{39}=\mathrm{0} \\ $$$$\left(\mathrm{4}{b}−\mathrm{14}\right)\left(\mathrm{3}{y}−\mathrm{13}\right)=\mathrm{12}{by}−\mathrm{52}{b}−\mathrm{42}{y}+\mathrm{182} \\ $$$$\Rightarrow\mathrm{10}{y}^{\mathrm{2}} +\left(−\mathrm{78}+\mathrm{12}{b}−\mathrm{42}−\mathrm{2}{b}\right){y}+\left(\mathrm{169}−\mathrm{52}{b}+\mathrm{182}−\mathrm{18}{b}+\mathrm{39}\right)=\mathrm{0} \\ $$$$\mathrm{10}{y}^{\mathrm{2}} +\left(\mathrm{10}{b}−\mathrm{120}\right){y}+\left(\mathrm{390}−\mathrm{70}{b}\right)=\mathrm{0} \\ $$$${y}^{\mathrm{2}} +\left({b}−\mathrm{12}\right){y}+\left(\mathrm{39}−\mathrm{7}{b}\right)=\mathrm{0} \\ $$$${only}\:\:{one}\:{sol} \\ $$$$\Rightarrow{D}=\left({b}−\mathrm{12}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{39}−\mathrm{7}{b}\right)=\mathrm{0} \\ $$$$\Rightarrow{b}^{\mathrm{2}} −\mathrm{24}{b}+\mathrm{144}+\mathrm{28}{b}−\mathrm{156}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} +\mathrm{4}{b}−\mathrm{12}=\mathrm{0} \\ $$$$\left({b}−\mathrm{2}\right)\left({b}+\mathrm{6}\right)=\mathrm{0} \\ $$$$\Rightarrow{b}=−\mathrm{6},\mathrm{2} \\ $$$$\Rightarrow{a}=\mathrm{19},\mathrm{3}\:\left({a}=\mathrm{7}−\mathrm{2}{b}\right) \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\mathrm{5}\left(\mathrm{36}+\mathrm{12}+\mathrm{2}\right),\mathrm{5}\left(\mathrm{4}−\mathrm{4}+\mathrm{2}\right)\:\left({r}^{\mathrm{2}} =\mathrm{5}\left({b}^{\mathrm{2}} −\mathrm{2}{b}+\mathrm{2}\right)\right) \\ $$$$\Rightarrow{r}=\mathrm{5}\sqrt{\mathrm{10}},\sqrt{\mathrm{10}} \\ $$$$\Rightarrow{c}_{\mathrm{1}} :\left({x}−\mathrm{19}\right)^{\mathrm{2}} +\left({y}+\mathrm{6}\right)^{\mathrm{2}} =\mathrm{250} \\ $$$$\Rightarrow{c}_{\mathrm{2}} :\left({x}−\mathrm{3}\right)^{\mathrm{2}} +\left({y}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{10} \\ $$

Commented by aleks041103 last updated on 02/Jun/22

Commented by nadovic last updated on 03/Jun/22

Thank you Sir

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Answered by cortano1 last updated on 03/Jun/22

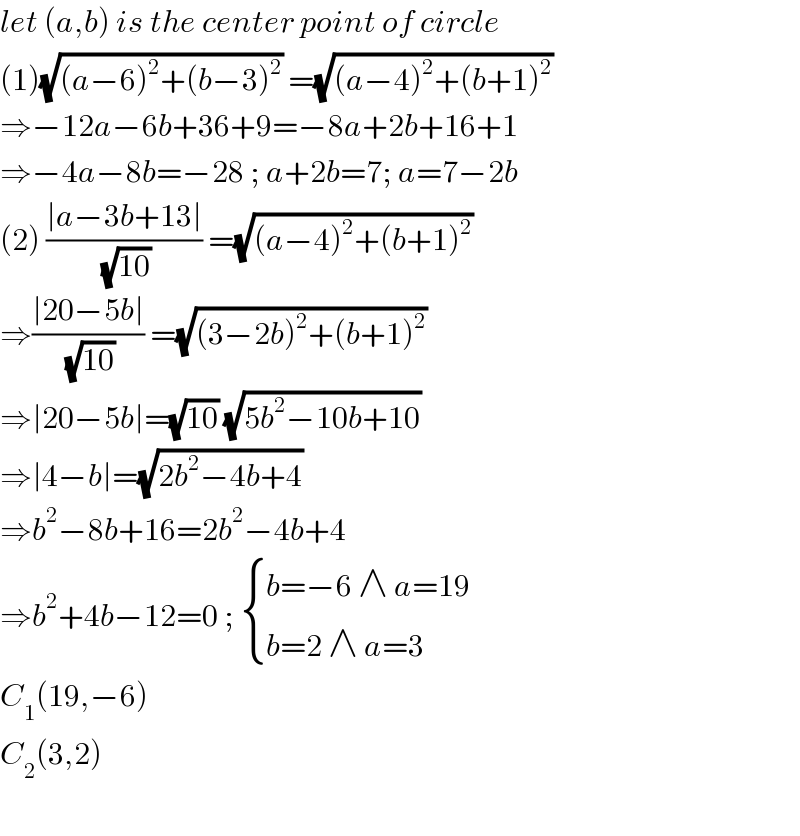
let (a,b) is the center point of circle (1)(√((a−6)^2 +(b−3)^2 )) =(√((a−4)^2 +(b+1)^2 )) ⇒−12a−6b+36+9=−8a+2b+16+1 ⇒−4a−8b=−28 ; a+2b=7; a=7−2b (2) ((∣a−3b+13∣)/( (√(10)))) =(√((a−4)^2 +(b+1)^2 )) ⇒((∣20−5b∣)/( (√(10)))) =(√((3−2b)^2 +(b+1)^2 )) ⇒∣20−5b∣=(√(10)) (√(5b^2 −10b+10)) ⇒∣4−b∣=(√(2b^2 −4b+4)) ⇒b^2 −8b+16=2b^2 −4b+4 ⇒b^2 +4b−12=0 ; { ((b=−6 ∧ a=19)),((b=2 ∧ a=3)) :} C_1 (19,−6) C_2 (3,2)

$${let}\:\left({a},{b}\right)\:{is}\:{the}\:{center}\:{point}\:{of}\:{circle} \\ $$$$\left(\mathrm{1}\right)\sqrt{\left({a}−\mathrm{6}\right)^{\mathrm{2}} +\left({b}−\mathrm{3}\right)^{\mathrm{2}} }\:=\sqrt{\left({a}−\mathrm{4}\right)^{\mathrm{2}} +\left({b}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow−\mathrm{12}{a}−\mathrm{6}{b}+\mathrm{36}+\mathrm{9}=−\mathrm{8}{a}+\mathrm{2}{b}+\mathrm{16}+\mathrm{1} \\ $$$$\Rightarrow−\mathrm{4}{a}−\mathrm{8}{b}=−\mathrm{28}\:;\:{a}+\mathrm{2}{b}=\mathrm{7};\:{a}=\mathrm{7}−\mathrm{2}{b} \\ $$$$\left(\mathrm{2}\right)\:\frac{\mid{a}−\mathrm{3}{b}+\mathrm{13}\mid}{\:\sqrt{\mathrm{10}}}\:=\sqrt{\left({a}−\mathrm{4}\right)^{\mathrm{2}} +\left({b}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\mid\mathrm{20}−\mathrm{5}{b}\mid}{\:\sqrt{\mathrm{10}}}\:=\sqrt{\left(\mathrm{3}−\mathrm{2}{b}\right)^{\mathrm{2}} +\left({b}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\mid\mathrm{20}−\mathrm{5}{b}\mid=\sqrt{\mathrm{10}}\:\sqrt{\mathrm{5}{b}^{\mathrm{2}} −\mathrm{10}{b}+\mathrm{10}} \\ $$$$\Rightarrow\mid\mathrm{4}−{b}\mid=\sqrt{\mathrm{2}{b}^{\mathrm{2}} −\mathrm{4}{b}+\mathrm{4}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} −\mathrm{8}{b}+\mathrm{16}=\mathrm{2}{b}^{\mathrm{2}} −\mathrm{4}{b}+\mathrm{4} \\ $$$$\Rightarrow{b}^{\mathrm{2}} +\mathrm{4}{b}−\mathrm{12}=\mathrm{0}\:;\:\begin{cases}{{b}=−\mathrm{6}\:\wedge\:{a}=\mathrm{19}}\\{{b}=\mathrm{2}\:\wedge\:{a}=\mathrm{3}}\end{cases} \\ $$$${C}_{\mathrm{1}} \left(\mathrm{19},−\mathrm{6}\right) \\ $$$${C}_{\mathrm{2}} \left(\mathrm{3},\mathrm{2}\right) \\ $$$$ \\ $$

Commented by nadovic last updated on 03/Jun/22

Thank you Sir

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com