Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 17093 by 1234Hello last updated on 02/Jul/17

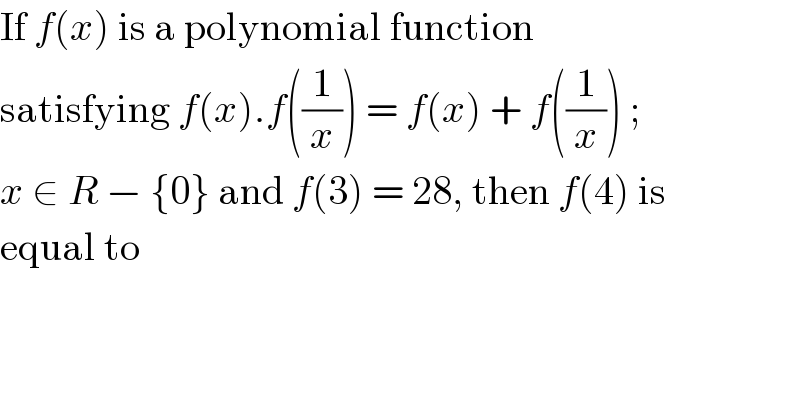
If f(x) is a polynomial function satisfying f(x).f((1/x)) = f(x) + f((1/x)) ; x ∈ R − {0} and f(3) = 28, then f(4) is equal to

$$\mathrm{If}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial}\:\mathrm{function} \\ $$$$\mathrm{satisfying}\:{f}\left({x}\right).{f}\left(\frac{\mathrm{1}}{{x}}\right)\:=\:{f}\left({x}\right)\:+\:{f}\left(\frac{\mathrm{1}}{{x}}\right)\:; \\ $$$${x}\:\in\:{R}\:−\:\left\{\mathrm{0}\right\}\:\mathrm{and}\:{f}\left(\mathrm{3}\right)\:=\:\mathrm{28},\:\mathrm{then}\:{f}\left(\mathrm{4}\right)\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to} \\ $$

Commented by prakash jain last updated on 30/Jun/17

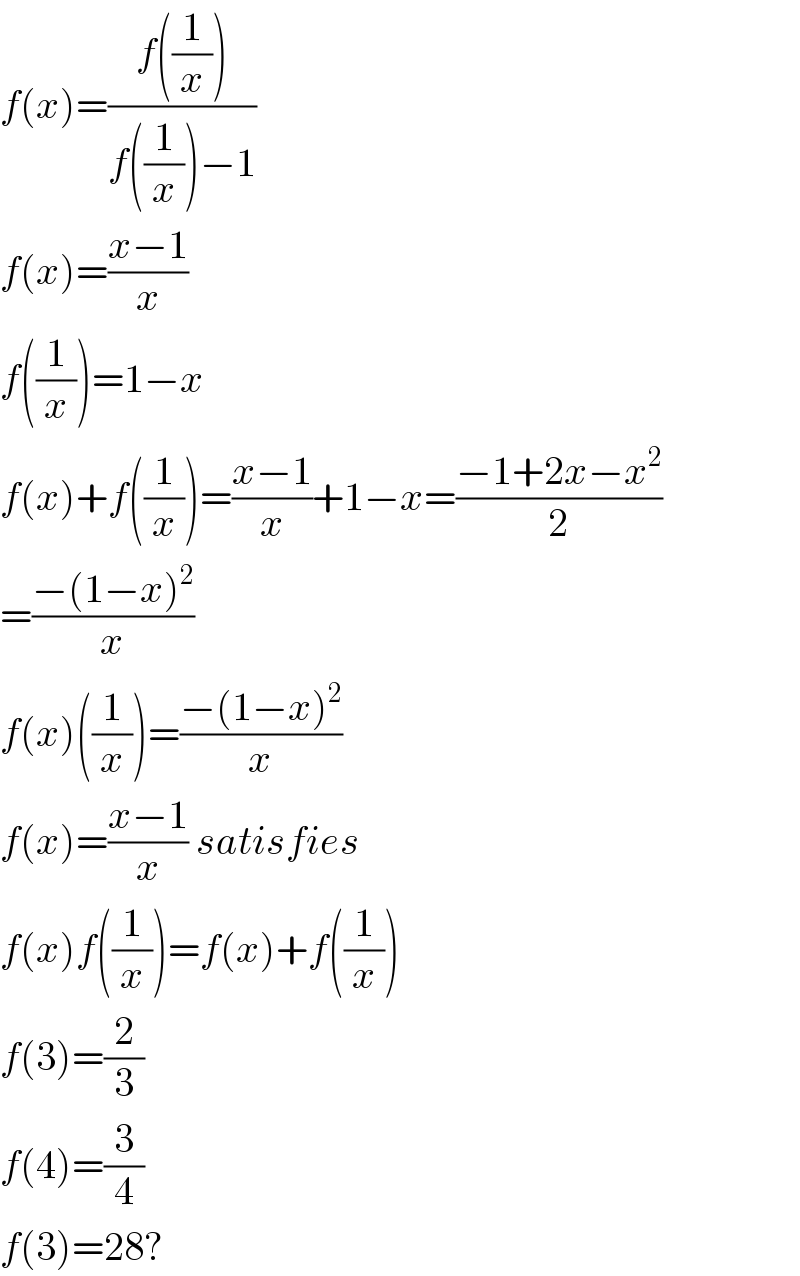
f(x)=((f((1/x)))/(f((1/x))−1)) f(x)=((x−1)/x) f((1/x))=1−x f(x)+f((1/x))=((x−1)/x)+1−x=((−1+2x−x^2 )/2) =((−(1−x)^2 )/x) f(x)((1/x))=((−(1−x)^2 )/x) f(x)=((x−1)/x) satisfies f(x)f((1/x))=f(x)+f((1/x)) f(3)=(2/3) f(4)=(3/4) f(3)=28?

$${f}\left({x}\right)=\frac{{f}\left(\frac{\mathrm{1}}{{x}}\right)}{{f}\left(\frac{\mathrm{1}}{{x}}\right)−\mathrm{1}} \\ $$$${f}\left({x}\right)=\frac{{x}−\mathrm{1}}{{x}} \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{1}−{x} \\ $$$${f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{{x}−\mathrm{1}}{{x}}+\mathrm{1}−{x}=\frac{−\mathrm{1}+\mathrm{2}{x}−{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\frac{−\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{{x}} \\ $$$${f}\left({x}\right)\left(\frac{\mathrm{1}}{{x}}\right)=\frac{−\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{{x}} \\ $$$${f}\left({x}\right)=\frac{{x}−\mathrm{1}}{{x}}\:{satisfies} \\ $$$${f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right)={f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$${f}\left(\mathrm{3}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${f}\left(\mathrm{4}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{28}? \\ $$

Commented by mrW1 last updated on 01/Jul/17

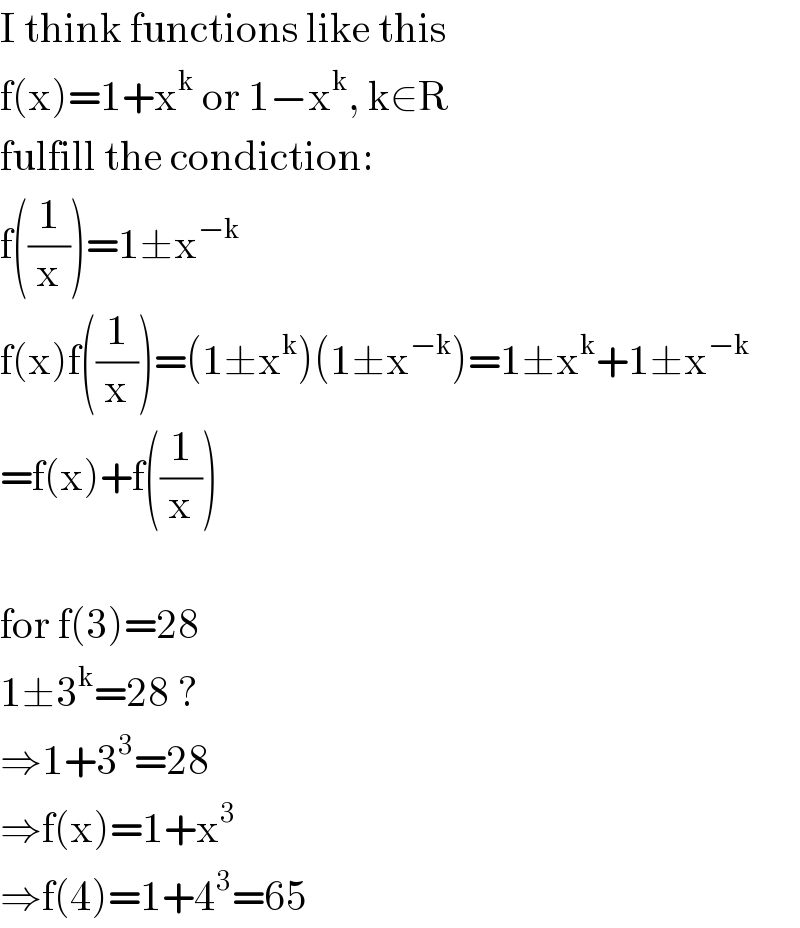
I think functions like this f(x)=1+x^k or 1−x^k , k∈R fulfill the condiction: f((1/x))=1±x^(−k) f(x)f((1/x))=(1±x^k )(1±x^(−k) )=1±x^k +1±x^(−k) =f(x)+f((1/x)) for f(3)=28 1±3^k =28 ? ⇒1+3^3 =28 ⇒f(x)=1+x^3 ⇒f(4)=1+4^3 =65

$$\mathrm{I}\:\mathrm{think}\:\mathrm{functions}\:\mathrm{like}\:\mathrm{this} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x}^{\mathrm{k}} \:\mathrm{or}\:\mathrm{1}−\mathrm{x}^{\mathrm{k}} ,\:\mathrm{k}\in\mathrm{R} \\ $$$$\mathrm{fulfill}\:\mathrm{the}\:\mathrm{condiction}: \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{1}\pm\mathrm{x}^{−\mathrm{k}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\left(\mathrm{1}\pm\mathrm{x}^{\mathrm{k}} \right)\left(\mathrm{1}\pm\mathrm{x}^{−\mathrm{k}} \right)=\mathrm{1}\pm\mathrm{x}^{\mathrm{k}} +\mathrm{1}\pm\mathrm{x}^{−\mathrm{k}} \\ $$$$=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$ \\ $$$$\mathrm{for}\:\mathrm{f}\left(\mathrm{3}\right)=\mathrm{28} \\ $$$$\mathrm{1}\pm\mathrm{3}^{\mathrm{k}} =\mathrm{28}\:? \\ $$$$\Rightarrow\mathrm{1}+\mathrm{3}^{\mathrm{3}} =\mathrm{28} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{4}\right)=\mathrm{1}+\mathrm{4}^{\mathrm{3}} =\mathrm{65} \\ $$

Commented by mrW1 last updated on 01/Jul/17

I started with f(x)=a+bx and got a=1 and b=±1 and then I replaced x with x^k without change the property of the function. I am not sure if there are other functions besides 1±x^k . if no, then the answer for the question is unique. e.g. if f(3)=−20 then 1−3^k =−20⇒k=((ln 21)/(ln 3))≈2.77 ⇒f(4)=1−4^k =−45.607. if f(3)=6⇒1+3^k =6⇒k=((ln 5)/(ln 3)) ⇒f(4)=1+4^k =8.62

$$\mathrm{I}\:\mathrm{started}\:\mathrm{with}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{a}+\mathrm{bx}\:\mathrm{and}\:\mathrm{got} \\ $$$$\mathrm{a}=\mathrm{1}\:\mathrm{and}\:\mathrm{b}=\pm\mathrm{1}\:\mathrm{and}\:\mathrm{then}\:\mathrm{I}\:\mathrm{replaced}\:\mathrm{x} \\ $$$$\mathrm{with}\:\mathrm{x}^{\mathrm{k}} \:\mathrm{without}\:\mathrm{change}\:\mathrm{the}\:\mathrm{property} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{function}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{there} \\ $$$$\mathrm{are}\:\mathrm{other}\:\mathrm{functions}\:\mathrm{besides}\:\mathrm{1}\pm\mathrm{x}^{\mathrm{k}} . \\ $$$$\mathrm{if}\:\mathrm{no},\:\mathrm{then}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{for}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is} \\ $$$$\mathrm{unique}. \\ $$$$\mathrm{e}.\mathrm{g}.\:\mathrm{if}\:\mathrm{f}\left(\mathrm{3}\right)=−\mathrm{20}\:\mathrm{then} \\ $$$$\mathrm{1}−\mathrm{3}^{\mathrm{k}} =−\mathrm{20}\Rightarrow\mathrm{k}=\frac{\mathrm{ln}\:\mathrm{21}}{\mathrm{ln}\:\mathrm{3}}\approx\mathrm{2}.\mathrm{77} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{4}\right)=\mathrm{1}−\mathrm{4}^{\mathrm{k}} =−\mathrm{45}.\mathrm{607}. \\ $$$$\mathrm{if}\:\mathrm{f}\left(\mathrm{3}\right)=\mathrm{6}\Rightarrow\mathrm{1}+\mathrm{3}^{\mathrm{k}} =\mathrm{6}\Rightarrow\mathrm{k}=\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{ln}\:\mathrm{3}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{4}\right)=\mathrm{1}+\mathrm{4}^{\mathrm{k}} =\mathrm{8}.\mathrm{62} \\ $$

Commented by Tinkutara last updated on 01/Jul/17

Thanks Sirs!

$$\mathrm{Thanks}\:\mathrm{Sirs}! \\ $$

Commented by prakash jain last updated on 01/Jul/17

it satisfies g(x)g((1/x))=1 and as you described f(x)=1±g(x) is valid solution. coming back to what is asked in question. Try an alternative f(x) g(x)=((10x−3)/(10−3x)) f(x)=((7x+7)/(10−3x))⇒f(3)=28 f((1/x))=((7+7x)/(10x−3)) f(x)+f((1/x))=((7x+7)/(10−3x))+((7+7x)/(10x−3)) =(((7x+7)(10x−3+10−3x))/((10−3x)(10x−3))) =(((7x+7)(7x+7))/((10−3x)(10x−3)))=f(x)f((1/x)) f(4)=((7×4+7)/(10−3×4))=−((35)/2)

$${it}\:{satisfies}\:{g}\left({x}\right){g}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{as}\:\mathrm{you}\:\mathrm{described} \\ $$$${f}\left({x}\right)=\mathrm{1}\pm{g}\left({x}\right)\:\mathrm{is}\:\mathrm{valid} \\ $$$$\mathrm{solution}. \\ $$$$\mathrm{coming}\:\mathrm{back}\:\mathrm{to}\:\mathrm{what}\:\mathrm{is}\:\mathrm{asked}\:\mathrm{in} \\ $$$$\mathrm{question}. \\ $$$$\mathrm{Try}\:\mathrm{an}\:\mathrm{alternative}\:{f}\left({x}\right) \\ $$$${g}\left({x}\right)=\frac{\mathrm{10}{x}−\mathrm{3}}{\mathrm{10}−\mathrm{3}{x}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{7}{x}+\mathrm{7}}{\mathrm{10}−\mathrm{3}{x}}\Rightarrow{f}\left(\mathrm{3}\right)=\mathrm{28} \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\mathrm{7}+\mathrm{7}{x}}{\mathrm{10}{x}−\mathrm{3}} \\ $$$${f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\mathrm{7}{x}+\mathrm{7}}{\mathrm{10}−\mathrm{3}{x}}+\frac{\mathrm{7}+\mathrm{7}{x}}{\mathrm{10}{x}−\mathrm{3}} \\ $$$$=\frac{\left(\mathrm{7}{x}+\mathrm{7}\right)\left(\mathrm{10}{x}−\mathrm{3}+\mathrm{10}−\mathrm{3}{x}\right)}{\left(\mathrm{10}−\mathrm{3}{x}\right)\left(\mathrm{10}{x}−\mathrm{3}\right)} \\ $$$$=\frac{\left(\mathrm{7}{x}+\mathrm{7}\right)\left(\mathrm{7}{x}+\mathrm{7}\right)}{\left(\mathrm{10}−\mathrm{3}{x}\right)\left(\mathrm{10}{x}−\mathrm{3}\right)}={f}\left({x}\right){f}\left(\frac{\mathrm{1}}{{x}}\right) \\ $$$${f}\left(\mathrm{4}\right)=\frac{\mathrm{7}×\mathrm{4}+\mathrm{7}}{\mathrm{10}−\mathrm{3}×\mathrm{4}}=−\frac{\mathrm{35}}{\mathrm{2}} \\ $$

Commented by prakash jain last updated on 01/Jul/17

Thanks, mrW1!

$$\mathrm{Thanks},\:\mathrm{mrW1}! \\ $$

Commented by mrW1 last updated on 01/Jul/17

Do you have any ideas if there are other types of functions with this property? I think the function should be of the form f(x)=1±g(x) then f((1/x))=1±g((1/x)) f(x)f((1/x))=[1±g(x)][1±g((1/x))] =1±g(x)+g(x)g((1/x))±g((1/x)) =f(x)+f((1/x)) if g(x)g((1/x))=1 g(x)=x^k fulfills this condition but are there any other function types for g(x)?

$$\mathrm{Do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{any}\:\mathrm{ideas}\:\mathrm{if}\:\mathrm{there}\:\mathrm{are}\:\mathrm{other} \\ $$$$\mathrm{types}\:\mathrm{of}\:\mathrm{functions}\:\mathrm{with}\:\mathrm{this}\:\mathrm{property}? \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{function}\:\mathrm{should}\:\mathrm{be}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{form}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}\pm\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{then} \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{1}\pm\mathrm{g}\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\left[\mathrm{1}\pm\mathrm{g}\left(\mathrm{x}\right)\right]\left[\mathrm{1}\pm\mathrm{g}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\right] \\ $$$$=\mathrm{1}\pm\mathrm{g}\left(\mathrm{x}\right)+\mathrm{g}\left(\mathrm{x}\right)\mathrm{g}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\pm\mathrm{g}\left(\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{if}\:\mathrm{g}\left(\mathrm{x}\right)\mathrm{g}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{k}} \:\mathrm{fulfills}\:\mathrm{this}\:\mathrm{condition} \\ $$$$\mathrm{but}\:\mathrm{are}\:\mathrm{there}\:\mathrm{any}\:\mathrm{other}\:\mathrm{function}\:\mathrm{types}\: \\ $$$$\mathrm{for}\:\mathrm{g}\left(\mathrm{x}\right)? \\ $$

Commented by prakash jain last updated on 01/Jul/17

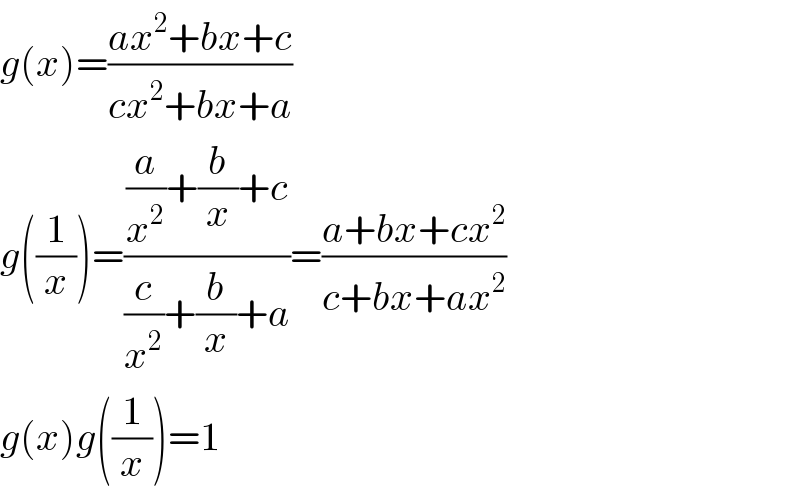
g(x)=((ax^2 +bx+c)/(cx^2 +bx+a)) g((1/x))=(((a/x^2 )+(b/x)+c)/((c/x^2 )+(b/x)+a))=((a+bx+cx^2 )/(c+bx+ax^2 )) g(x)g((1/x))=1

$${g}\left({x}\right)=\frac{{ax}^{\mathrm{2}} +{bx}+{c}}{{cx}^{\mathrm{2}} +{bx}+{a}} \\ $$$${g}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\frac{{a}}{{x}^{\mathrm{2}} }+\frac{{b}}{{x}}+{c}}{\frac{{c}}{{x}^{\mathrm{2}} }+\frac{{b}}{{x}}+{a}}=\frac{{a}+{bx}+{cx}^{\mathrm{2}} }{{c}+{bx}+{ax}^{\mathrm{2}} } \\ $$$${g}\left({x}\right){g}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{1} \\ $$

Commented by mrW1 last updated on 01/Jul/17

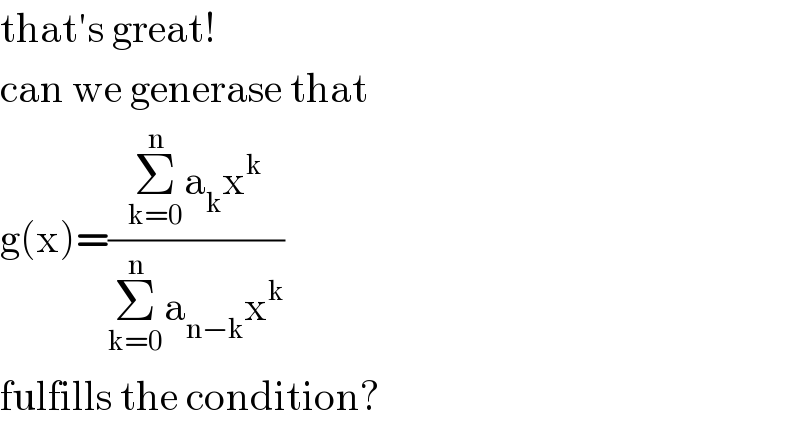
that′s great! can we generase that g(x)=((Σ_(k=0) ^n a_k x^k )/(Σ_(k=0) ^n a_(n−k) x^k )) fulfills the condition?

$$\mathrm{that}'\mathrm{s}\:\mathrm{great}! \\ $$$$\mathrm{can}\:\mathrm{we}\:\mathrm{generase}\:\mathrm{that} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\frac{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{x}^{\mathrm{k}} }{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{n}−\mathrm{k}} \mathrm{x}^{\mathrm{k}} } \\ $$$$\mathrm{fulfills}\:\mathrm{the}\:\mathrm{condition}? \\ $$

Commented by mrW1 last updated on 01/Jul/17

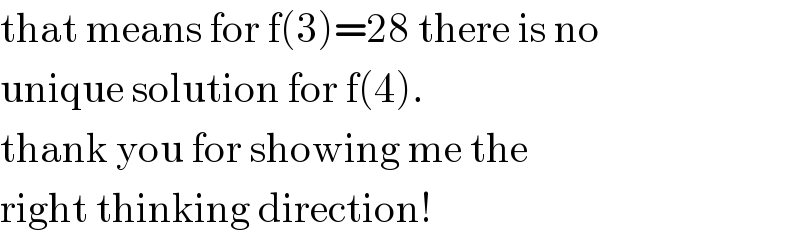
that means for f(3)=28 there is no unique solution for f(4). thank you for showing me the right thinking direction!

$$\mathrm{that}\:\mathrm{means}\:\mathrm{for}\:\mathrm{f}\left(\mathrm{3}\right)=\mathrm{28}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no} \\ $$$$\mathrm{unique}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{f}\left(\mathrm{4}\right). \\ $$$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{showing}\:\mathrm{me}\:\mathrm{the} \\ $$$$\mathrm{right}\:\mathrm{thinking}\:\mathrm{direction}! \\ $$

Commented by 1234Hello last updated on 02/Jul/17

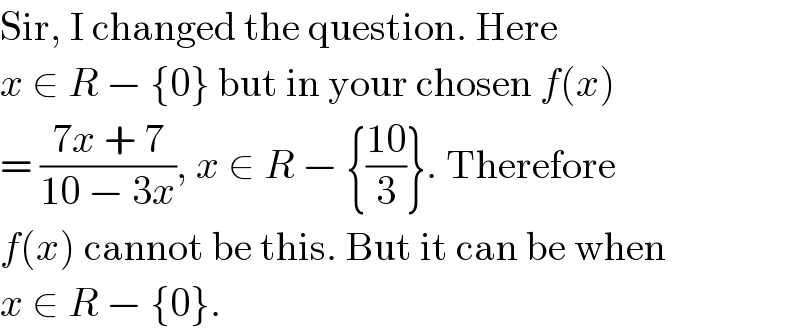
Sir, I changed the question. Here x ∈ R − {0} but in your chosen f(x) = ((7x + 7)/(10 − 3x)), x ∈ R − {((10)/3)}. Therefore f(x) cannot be this. But it can be when x ∈ R − {0}.

$$\mathrm{Sir},\:\mathrm{I}\:\mathrm{changed}\:\mathrm{the}\:\mathrm{question}.\:\mathrm{Here} \\ $$$${x}\:\in\:{R}\:−\:\left\{\mathrm{0}\right\}\:\mathrm{but}\:\mathrm{in}\:\mathrm{your}\:\mathrm{chosen}\:{f}\left({x}\right) \\ $$$$=\:\frac{\mathrm{7}{x}\:+\:\mathrm{7}}{\mathrm{10}\:−\:\mathrm{3}{x}},\:{x}\:\in\:{R}\:−\:\left\{\frac{\mathrm{10}}{\mathrm{3}}\right\}.\:\mathrm{Therefore} \\ $$$${f}\left({x}\right)\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{this}.\:\mathrm{But}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{when} \\ $$$${x}\:\in\:{R}\:−\:\left\{\mathrm{0}\right\}. \\ $$

Commented by prakash jain last updated on 02/Jul/17

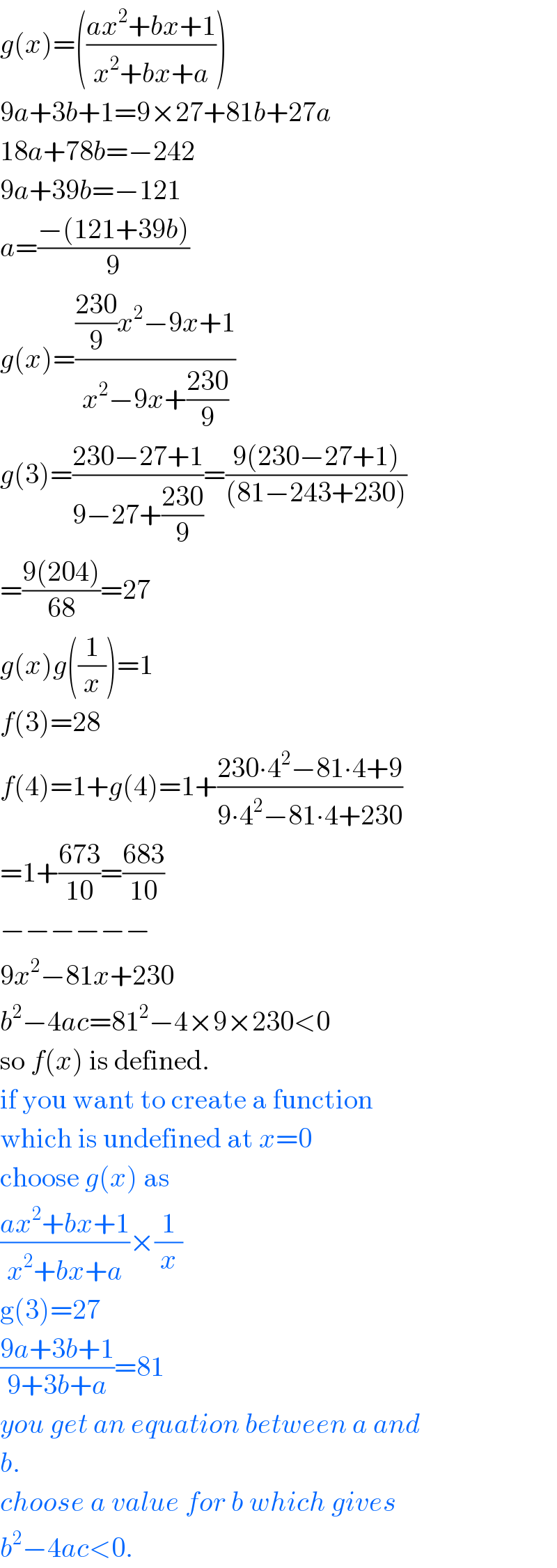
g(x)=(((ax^2 +bx+1)/(x^2 +bx+a))) 9a+3b+1=9×27+81b+27a 18a+78b=−242 9a+39b=−121 a=((−(121+39b))/9) g(x)=((((230)/9)x^2 −9x+1)/(x^2 −9x+((230)/9))) g(3)=((230−27+1)/(9−27+((230)/9)))=((9(230−27+1))/((81−243+230))) =((9(204))/(68))=27 g(x)g((1/x))=1 f(3)=28 f(4)=1+g(4)=1+((230∙4^2 −81∙4+9)/(9∙4^2 −81∙4+230)) =1+((673)/(10))=((683)/(10)) −−−−−− 9x^2 −81x+230 b^2 −4ac=81^2 −4×9×230<0 so f(x) is defined. if you want to create a function which is undefined at x=0 choose g(x) as ((ax^2 +bx+1)/(x^2 +bx+a))×(1/x) g(3)=27 ((9a+3b+1)/(9+3b+a))=81 you get an equation between a and b. choose a value for b which gives b^2 −4ac<0.

$${g}\left({x}\right)=\left(\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{1}}{{x}^{\mathrm{2}} +{bx}+{a}}\right) \\ $$$$\mathrm{9}{a}+\mathrm{3}{b}+\mathrm{1}=\mathrm{9}×\mathrm{27}+\mathrm{81}{b}+\mathrm{27}{a} \\ $$$$\mathrm{18}{a}+\mathrm{78}{b}=−\mathrm{242} \\ $$$$\mathrm{9}{a}+\mathrm{39}{b}=−\mathrm{121} \\ $$$${a}=\frac{−\left(\mathrm{121}+\mathrm{39}{b}\right)}{\mathrm{9}} \\ $$$${g}\left({x}\right)=\frac{\frac{\mathrm{230}}{\mathrm{9}}{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{9}{x}+\frac{\mathrm{230}}{\mathrm{9}}} \\ $$$${g}\left(\mathrm{3}\right)=\frac{\mathrm{230}−\mathrm{27}+\mathrm{1}}{\mathrm{9}−\mathrm{27}+\frac{\mathrm{230}}{\mathrm{9}}}=\frac{\mathrm{9}\left(\mathrm{230}−\mathrm{27}+\mathrm{1}\right)}{\left(\mathrm{81}−\mathrm{243}+\mathrm{230}\right)} \\ $$$$=\frac{\mathrm{9}\left(\mathrm{204}\right)}{\mathrm{68}}=\mathrm{27} \\ $$$${g}\left({x}\right){g}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{28} \\ $$$${f}\left(\mathrm{4}\right)=\mathrm{1}+{g}\left(\mathrm{4}\right)=\mathrm{1}+\frac{\mathrm{230}\centerdot\mathrm{4}^{\mathrm{2}} −\mathrm{81}\centerdot\mathrm{4}+\mathrm{9}}{\mathrm{9}\centerdot\mathrm{4}^{\mathrm{2}} −\mathrm{81}\centerdot\mathrm{4}+\mathrm{230}} \\ $$$$=\mathrm{1}+\frac{\mathrm{673}}{\mathrm{10}}=\frac{\mathrm{683}}{\mathrm{10}} \\ $$$$−−−−−− \\ $$$$\mathrm{9}{x}^{\mathrm{2}} −\mathrm{81}{x}+\mathrm{230} \\ $$$${b}^{\mathrm{2}} −\mathrm{4}{ac}=\mathrm{81}^{\mathrm{2}} −\mathrm{4}×\mathrm{9}×\mathrm{230}<\mathrm{0} \\ $$$$\mathrm{so}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{defined}. \\ $$$$\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{create}\:\mathrm{a}\:\mathrm{function} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{undefined}\:\mathrm{at}\:{x}=\mathrm{0} \\ $$$$\mathrm{choose}\:{g}\left({x}\right)\:\mathrm{as} \\ $$$$\frac{{ax}^{\mathrm{2}} +{bx}+\mathrm{1}}{{x}^{\mathrm{2}} +{bx}+{a}}×\frac{\mathrm{1}}{{x}} \\ $$$$\mathrm{g}\left(\mathrm{3}\right)=\mathrm{27} \\ $$$$\frac{\mathrm{9}{a}+\mathrm{3}{b}+\mathrm{1}}{\mathrm{9}+\mathrm{3}{b}+{a}}=\mathrm{81} \\ $$$${you}\:{get}\:{an}\:{equation}\:{between}\:{a}\:{and} \\ $$$${b}. \\ $$$${choose}\:{a}\:{value}\:{for}\:{b}\:{which}\:{gives} \\ $$$${b}^{\mathrm{2}} −\mathrm{4}{ac}<\mathrm{0}. \\ $$

Commented by mrW1 last updated on 02/Jul/17

since there are infinite possible functions: f(x) =1±((Σ_(k=0) ^n a_k x^k )/(Σ_(k=0) ^n a_(n−k) x^k )) with n∈N and a_0 ,a_1 ,...,a_n ∈R there is no unique solution for (n,a_0 ,a_1 ,...,a_n ) from the only one equation f(3) =1±((Σ_(k=0) ^n a_k 3^k )/(Σ_(k=0) ^n a_(n−k) 3^k ))=28 therefore there is also no unique value for f(4): f(4) =1±((Σ_(k=0) ^n a_k 4^k )/(Σ_(k=0) ^n a_(n−k) 4^k ))

$$\mathrm{since}\:\mathrm{there}\:\mathrm{are}\:\mathrm{infinite}\:\mathrm{possible}\:\mathrm{functions}: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{1}\pm\frac{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{x}^{\mathrm{k}} }{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{n}−\mathrm{k}} \mathrm{x}^{\mathrm{k}} } \\ $$$$\mathrm{with}\:\mathrm{n}\in\mathbb{N}\:\mathrm{and}\:\mathrm{a}_{\mathrm{0}} ,\mathrm{a}_{\mathrm{1}} ,...,\mathrm{a}_{\mathrm{n}} \in\mathbb{R} \\ $$$$ \\ $$$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{unique}\:\mathrm{solution}\:\mathrm{for}\: \\ $$$$\left(\mathrm{n},\mathrm{a}_{\mathrm{0}} ,\mathrm{a}_{\mathrm{1}} ,...,\mathrm{a}_{\mathrm{n}} \right)\:\mathrm{from}\:\mathrm{the}\:\mathrm{only}\:\mathrm{one}\:\mathrm{equation} \\ $$$$\mathrm{f}\left(\mathrm{3}\right)\:=\mathrm{1}\pm\frac{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{3}^{\mathrm{k}} }{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{n}−\mathrm{k}} \mathrm{3}^{\mathrm{k}} }=\mathrm{28} \\ $$$$ \\ $$$$\mathrm{therefore}\:\mathrm{there}\:\mathrm{is}\:\mathrm{also}\:\mathrm{no}\:\mathrm{unique} \\ $$$$\mathrm{value}\:\mathrm{for}\:\mathrm{f}\left(\mathrm{4}\right): \\ $$$$\mathrm{f}\left(\mathrm{4}\right)\:=\mathrm{1}\pm\frac{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{4}^{\mathrm{k}} }{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{n}−\mathrm{k}} \mathrm{4}^{\mathrm{k}} } \\ $$

Commented by prakash jain last updated on 02/Jul/17

Ok. I missed some part in the question. The question is specifically asking for polynomial function. f(x)=1+x^3 is only correct answer.

$$\mathrm{Ok}.\:\mathrm{I}\:\mathrm{missed}\:\mathrm{some}\:\mathrm{part}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{question}.\:\mathrm{The}\:\mathrm{question}\:\mathrm{is} \\ $$$$\mathrm{specifically}\:\mathrm{asking}\:\mathrm{for}\:\mathrm{polynomial} \\ $$$$\mathrm{function}. \\ $$$${f}\left({x}\right)=\mathrm{1}+{x}^{\mathrm{3}} \:\mathrm{is}\:\mathrm{only}\:\mathrm{correct}\:\mathrm{answer}. \\ $$

Commented by mrW1 last updated on 02/Jul/17

to 1234hello: I think the original question was much more interesting and challenging than now. Even though there was no unique answer but one may think in all directions. I see it as a great gain from your original question that we know now that the requested function which satisfies the functional equation could and must be of the form f(x)=1±((Σ_(k=0) ^n a_k x^k )/(Σ_(k=0) ^n a_(n−k) x^k )). We hadn′t lernt so much if you had said from very begining that f(x) is a polynominal function, because that would have restricted the direction for our thinking.

$$\mathrm{to}\:\mathrm{1234hello}: \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{original}\:\mathrm{question}\:\mathrm{was}\:\mathrm{much} \\ $$$$\mathrm{more}\:\mathrm{interesting}\:\mathrm{and}\:\mathrm{challenging} \\ $$$$\mathrm{than}\:\mathrm{now}.\:\mathrm{Even}\:\mathrm{though}\:\mathrm{there}\:\mathrm{was}\:\mathrm{no} \\ $$$$\mathrm{unique}\:\mathrm{answer}\:\mathrm{but}\:\mathrm{one}\:\mathrm{may}\:\mathrm{think}\:\mathrm{in} \\ $$$$\mathrm{all}\:\mathrm{directions}.\:\mathrm{I}\:\mathrm{see}\:\mathrm{it}\:\mathrm{as}\:\mathrm{a}\:\mathrm{great}\:\mathrm{gain} \\ $$$$\mathrm{from}\:\mathrm{your}\:\mathrm{original}\:\mathrm{question}\:\mathrm{that}\:\mathrm{we} \\ $$$$\mathrm{know}\:\mathrm{now}\:\mathrm{that}\:\mathrm{the}\:\mathrm{requested} \\ $$$$\mathrm{function}\:\mathrm{which}\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{functional} \\ $$$$\mathrm{equation}\:\mathrm{could}\:\mathrm{and}\:\mathrm{must}\:\mathrm{be}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}\pm\frac{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{k}} \mathrm{x}^{\mathrm{k}} }{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{n}−\mathrm{k}} \mathrm{x}^{\mathrm{k}} }. \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{hadn}'\mathrm{t}\:\mathrm{lernt}\:\mathrm{so}\:\mathrm{much}\:\mathrm{if}\:\mathrm{you}\:\mathrm{had} \\ $$$$\mathrm{said}\:\mathrm{from}\:\mathrm{very}\:\mathrm{begining}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{polynominal}\:\mathrm{function},\:\mathrm{because} \\ $$$$\mathrm{that}\:\mathrm{would}\:\mathrm{have}\:\mathrm{restricted}\:\mathrm{the}\:\mathrm{direction} \\ $$$$\mathrm{for}\:\mathrm{our}\:\mathrm{thinking}. \\ $$

Commented by 1234Hello last updated on 03/Jul/17

But this was the original question! I was in a hurry so I first posted that version. Thanks all for your efforts!

$$\mathrm{But}\:\mathrm{this}\:\mathrm{was}\:\mathrm{the}\:\mathrm{original}\:\mathrm{question}!\:\mathrm{I} \\ $$$$\mathrm{was}\:\mathrm{in}\:\mathrm{a}\:\mathrm{hurry}\:\mathrm{so}\:\mathrm{I}\:\mathrm{first}\:\mathrm{posted}\:\mathrm{that} \\ $$$$\mathrm{version}.\:\mathrm{Thanks}\:\mathrm{all}\:\mathrm{for}\:\mathrm{your}\:\mathrm{efforts}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com