Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 171090 by Kodjo last updated on 07/Jun/22

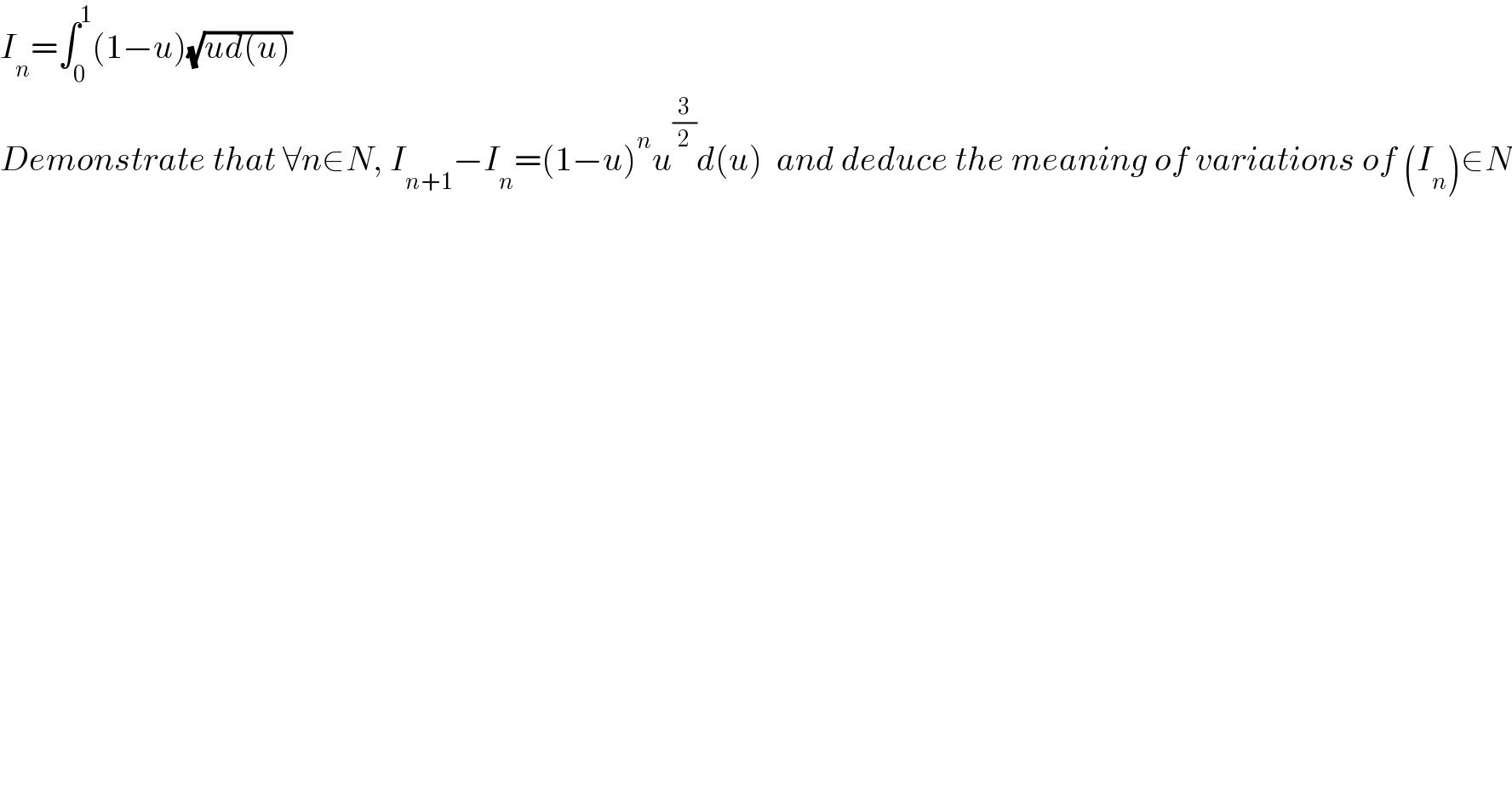
I_n =∫_0 ^1 (1−u)(√(ud(u))) Demonstrate that ∀n∈N, I_(n+1) −I_n =(1−u)^n u^(3/2) d(u) and deduce the meaning of variations of (I_n )∈N

$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)\sqrt{{ud}\left({u}\right)} \\ $$$${Demonstrate}\:{that}\:\forall{n}\in{N},\:{I}_{{n}+\mathrm{1}} −{I}_{{n}} =\left(\mathrm{1}−{u}\right)^{{n}} {u}^{\frac{\mathrm{3}}{\mathrm{2}}} {d}\left({u}\right)\:\:{and}\:{deduce}\:{the}\:{meaning}\:{of}\:{variations}\:{of}\:\left({I}_{{n}} \right)\in{N} \\ $$

Commented by Kodjo last updated on 07/Jun/22

Excuse me it's a mistake here is the real subject

Commented by Kodjo last updated on 07/Jun/22

Commented by Kodjo last updated on 07/Jun/22

Answered by aleks041103 last updated on 09/Jun/22

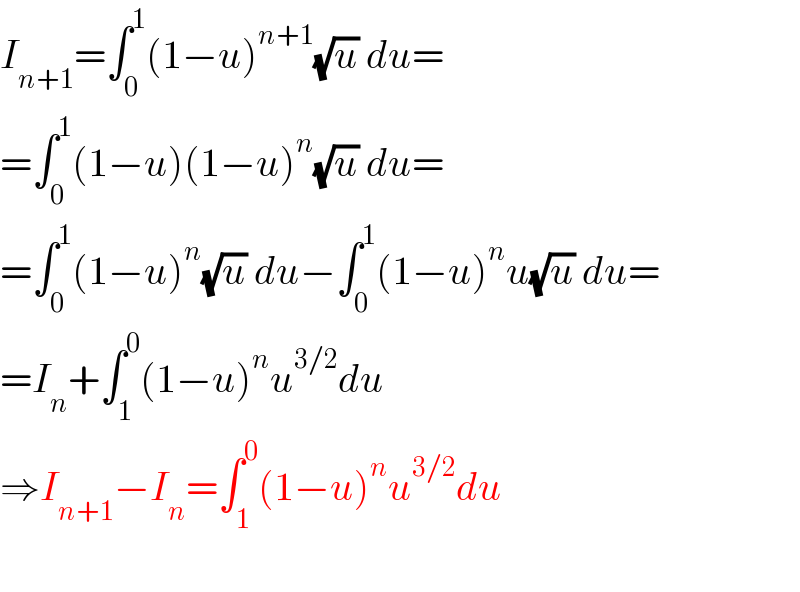
I_(n+1) =∫_0 ^1 (1−u)^(n+1) (√u) du= =∫_0 ^1 (1−u)(1−u)^n (√u) du= =∫_0 ^1 (1−u)^n (√u) du−∫_0 ^1 (1−u)^n u(√u) du= =I_n +∫_1 ^0 (1−u)^n u^(3/2) du ⇒I_(n+1) −I_n =∫_1 ^0 (1−u)^n u^(3/2) du

$${I}_{{n}+\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}+\mathrm{1}} \sqrt{{u}}\:{du}= \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)\left(\mathrm{1}−{u}\right)^{{n}} \sqrt{{u}}\:{du}= \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} \sqrt{{u}}\:{du}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} {u}\sqrt{{u}}\:{du}= \\ $$$$={I}_{{n}} +\int_{\mathrm{1}} ^{\mathrm{0}} \left(\mathrm{1}−{u}\right)^{{n}} {u}^{\mathrm{3}/\mathrm{2}} {du} \\ $$$$\Rightarrow{I}_{{n}+\mathrm{1}} −{I}_{{n}} =\int_{\mathrm{1}} ^{\mathrm{0}} \left(\mathrm{1}−{u}\right)^{{n}} {u}^{\mathrm{3}/\mathrm{2}} {du} \\ $$$$ \\ $$

Commented by aleks041103 last updated on 09/Jun/22

I_(n+1) =∫_0 ^1 (1−u)^(n+1) u^(1/2) du= =∫_0 ^1 (1−u)^(n+1) d((2/3)u^(3/2) )= ={(2/3)u^(3/2) (1−u)^(n+1) }_0 ^1 −((2(n+1))/3)∫_1 ^0 (1−u)^n u^(3/2) du= =−((2(n+1))/3)(I_(n+1) −I_n ) ⇒((2n+5)/3)I_(n+1) =((2n+2)/3)I_n ⇒I_(n+1) =((2n+2)/(2n+5))I_n ⇒I_n =((2n)/(2n+3)) ((2n−2)/(2n+1)) ... ((2.0+2)/(2.0+5))I_0 I_0 =∫_0 ^1 (√u)du=(2/3)u^(3/2) ]_0 ^1 =(2/3) ⇒I_n =((2.2.4.6. ... . 2n)/(3.5.7. ... .(2n+3)))=((2.2^n (1.2. ... .n))/((2n+3)!!)) I_n =((2^(n+1) n!)/((2n+3)!!)) but (2n+1)!!=1.3. ... .(2n−1)(2n+1)= =((1.2.3. ... .(2n−1)(2n)(2n+1))/(2.4. ... .(2n−2)(2n)))= =(((2n+1)!)/(2^n n!)) ⇒(2n+3)!!=(2(n+1)+1)!!=(((2n+3)!)/(2^(n+1) (n+1)!)) ⇒I_n =((4^(n+1) (n+1)!(n!))/((2n+3)!))

$${I}_{{n}+\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}+\mathrm{1}} {u}^{\mathrm{1}/\mathrm{2}} {du}= \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}+\mathrm{1}} {d}\left(\frac{\mathrm{2}}{\mathrm{3}}{u}^{\mathrm{3}/\mathrm{2}} \right)= \\ $$$$=\left\{\frac{\mathrm{2}}{\mathrm{3}}{u}^{\mathrm{3}/\mathrm{2}} \left(\mathrm{1}−{u}\right)^{{n}+\mathrm{1}} \right\}_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{\mathrm{3}}\int_{\mathrm{1}} ^{\mathrm{0}} \left(\mathrm{1}−{u}\right)^{{n}} {u}^{\mathrm{3}/\mathrm{2}} {du}= \\ $$$$=−\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{\mathrm{3}}\left({I}_{{n}+\mathrm{1}} −{I}_{{n}} \right) \\ $$$$\Rightarrow\frac{\mathrm{2}{n}+\mathrm{5}}{\mathrm{3}}{I}_{{n}+\mathrm{1}} =\frac{\mathrm{2}{n}+\mathrm{2}}{\mathrm{3}}{I}_{{n}} \\ $$$$\Rightarrow{I}_{{n}+\mathrm{1}} =\frac{\mathrm{2}{n}+\mathrm{2}}{\mathrm{2}{n}+\mathrm{5}}{I}_{{n}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{3}}\:\frac{\mathrm{2}{n}−\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:...\:\frac{\mathrm{2}.\mathrm{0}+\mathrm{2}}{\mathrm{2}.\mathrm{0}+\mathrm{5}}{I}_{\mathrm{0}} \\ $$$$\left.{I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{u}}{du}=\frac{\mathrm{2}}{\mathrm{3}}{u}^{\mathrm{3}/\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}.\mathrm{2}.\mathrm{4}.\mathrm{6}.\:...\:.\:\mathrm{2}{n}}{\mathrm{3}.\mathrm{5}.\mathrm{7}.\:...\:.\left(\mathrm{2}{n}+\mathrm{3}\right)}=\frac{\mathrm{2}.\mathrm{2}^{{n}} \left(\mathrm{1}.\mathrm{2}.\:...\:.{n}\right)}{\left(\mathrm{2}{n}+\mathrm{3}\right)!!} \\ $$$${I}_{{n}} =\frac{\mathrm{2}^{{n}+\mathrm{1}} {n}!}{\left(\mathrm{2}{n}+\mathrm{3}\right)!!} \\ $$$${but} \\ $$$$\left(\mathrm{2}{n}+\mathrm{1}\right)!!=\mathrm{1}.\mathrm{3}.\:...\:.\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)= \\ $$$$=\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}.\:...\:.\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{2}.\mathrm{4}.\:...\:.\left(\mathrm{2}{n}−\mathrm{2}\right)\left(\mathrm{2}{n}\right)}= \\ $$$$=\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{\mathrm{2}^{{n}} {n}!} \\ $$$$\Rightarrow\left(\mathrm{2}{n}+\mathrm{3}\right)!!=\left(\mathrm{2}\left({n}+\mathrm{1}\right)+\mathrm{1}\right)!!=\frac{\left(\mathrm{2}{n}+\mathrm{3}\right)!}{\mathrm{2}^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)!} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{4}^{{n}+\mathrm{1}} \left({n}+\mathrm{1}\right)!\left({n}!\right)}{\left(\mathrm{2}{n}+\mathrm{3}\right)!} \\ $$

Commented by Kodjo last updated on 09/Jun/22

Thanks

$${Thanks} \\ $$

Commented by ilhamQ last updated on 11/Jun/22

]]]]]]]

$$\left.\right]\left.\right]\left.\right]\left.\right]\left.\right]\left.\right]\left.\right] \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com