Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 171199 by mr W last updated on 09/Jun/22

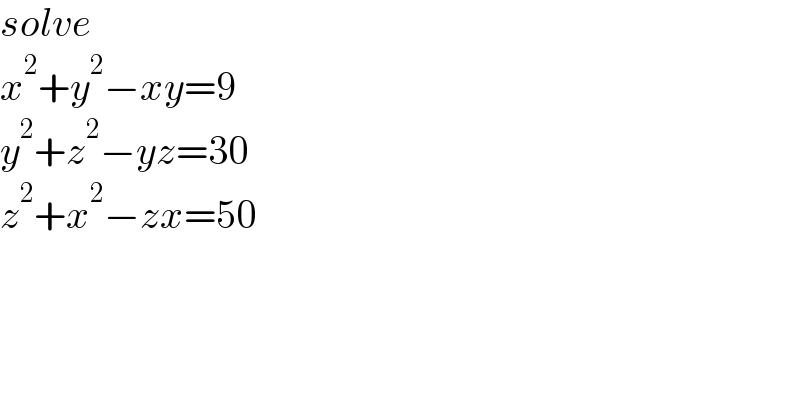
solve x^2 +y^2 −xy=9 y^2 +z^2 −yz=30 z^2 +x^2 −zx=50

solvex2+y2−xy=9y2+z2−yz=30z2+x2−zx=50

Commented by MJS_new last updated on 10/Jun/22

this has no “nice” solution...

thishasno‘‘nice″solution...

Answered by aleks041103 last updated on 10/Jun/22

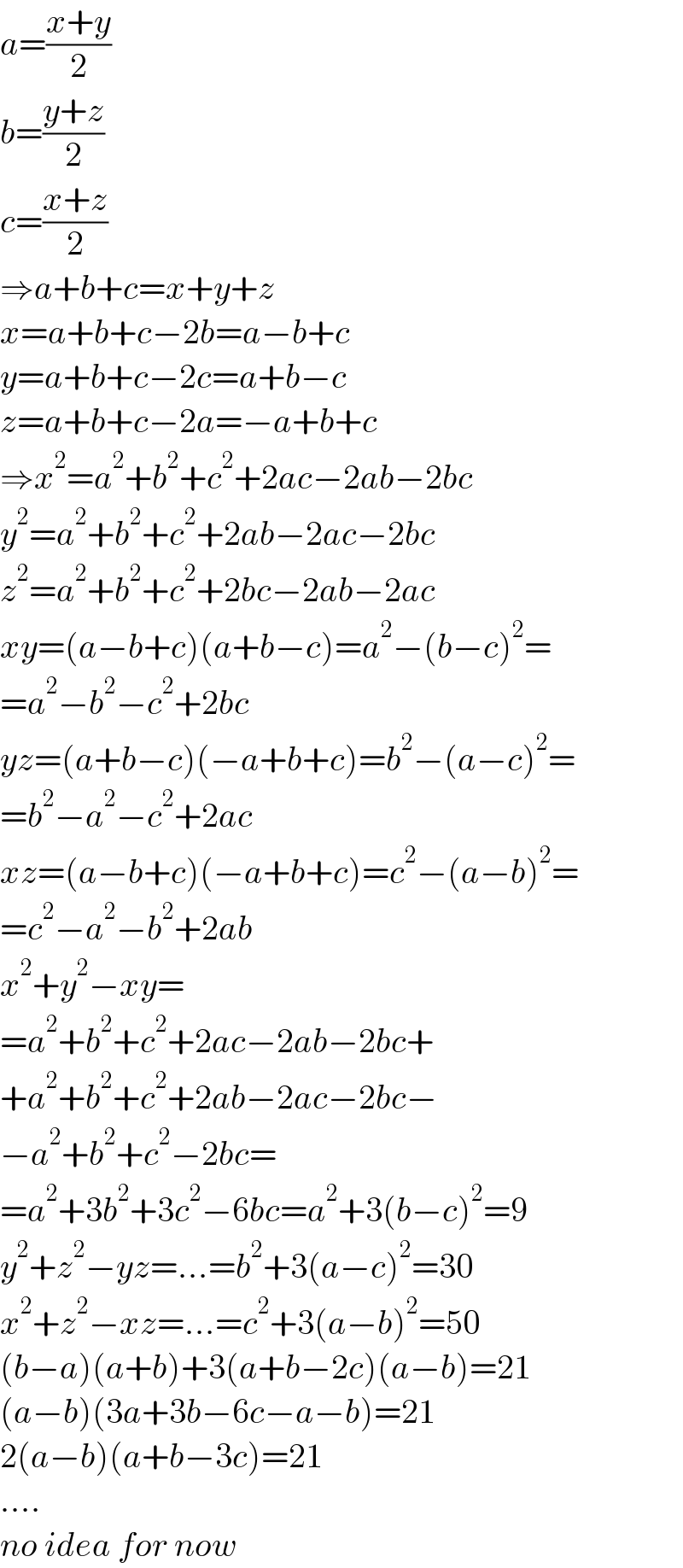
a=((x+y)/2) b=((y+z)/2) c=((x+z)/2) ⇒a+b+c=x+y+z x=a+b+c−2b=a−b+c y=a+b+c−2c=a+b−c z=a+b+c−2a=−a+b+c ⇒x^2 =a^2 +b^2 +c^2 +2ac−2ab−2bc y^2 =a^2 +b^2 +c^2 +2ab−2ac−2bc z^2 =a^2 +b^2 +c^2 +2bc−2ab−2ac xy=(a−b+c)(a+b−c)=a^2 −(b−c)^2 = =a^2 −b^2 −c^2 +2bc yz=(a+b−c)(−a+b+c)=b^2 −(a−c)^2 = =b^2 −a^2 −c^2 +2ac xz=(a−b+c)(−a+b+c)=c^2 −(a−b)^2 = =c^2 −a^2 −b^2 +2ab x^2 +y^2 −xy= =a^2 +b^2 +c^2 +2ac−2ab−2bc+ +a^2 +b^2 +c^2 +2ab−2ac−2bc− −a^2 +b^2 +c^2 −2bc= =a^2 +3b^2 +3c^2 −6bc=a^2 +3(b−c)^2 =9 y^2 +z^2 −yz=...=b^2 +3(a−c)^2 =30 x^2 +z^2 −xz=...=c^2 +3(a−b)^2 =50 (b−a)(a+b)+3(a+b−2c)(a−b)=21 (a−b)(3a+3b−6c−a−b)=21 2(a−b)(a+b−3c)=21 .... no idea for now

a=x+y2b=y+z2c=x+z2⇒a+b+c=x+y+zx=a+b+c−2b=a−b+cy=a+b+c−2c=a+b−cz=a+b+c−2a=−a+b+c⇒x2=a2+b2+c2+2ac−2ab−2bcy2=a2+b2+c2+2ab−2ac−2bcz2=a2+b2+c2+2bc−2ab−2acxy=(a−b+c)(a+b−c)=a2−(b−c)2==a2−b2−c2+2bcyz=(a+b−c)(−a+b+c)=b2−(a−c)2==b2−a2−c2+2acxz=(a−b+c)(−a+b+c)=c2−(a−b)2==c2−a2−b2+2abx2+y2−xy==a2+b2+c2+2ac−2ab−2bc++a2+b2+c2+2ab−2ac−2bc−−a2+b2+c2−2bc==a2+3b2+3c2−6bc=a2+3(b−c)2=9y2+z2−yz=...=b2+3(a−c)2=30x2+z2−xz=...=c2+3(a−b)2=50(b−a)(a+b)+3(a+b−2c)(a−b)=21(a−b)(3a+3b−6c−a−b)=212(a−b)(a+b−3c)=21....noideafornow

Commented by Tawa11 last updated on 11/Jun/22

Nice try sir. Weldone.

Nicetrysir.Weldone.

Answered by MJS_new last updated on 12/Jun/22

let y=px∧z=qx ⇒ x^2 =(9/(p^2 −p+1))=((30)/(p^2 −pq+q^2 ))=((50)/(q^2 −q+1)) (I) (II) (III) from I=II∧II=III we get q=((29p^2 −20p+11)/(9(p−1))) inserting this leads to p^4 −((71)/(391))p^3 −((240)/(391))p^2 +((469)/(391))p−((149)/(391))=0 this has no “nice”solution p_1 ≈−1.25724339 ⇒ q_1 ≈−4.03560259 p_2 ≈.383450177 ⇒ q_2 ≈−1.36872485 p_(3, 4) ≈.527689447±.715546104i ⇒ q_(3, 4) ≈1.27249620±.142489563i ⇒ x_1 ≈1.53134901 y_1 ≈−1.92527842 z_1 ≈−6.17991602 x_2 ≈3.43315083 y_2 ≈1.31644230 z_2 ≈−4.69903886 x_(3, 4) ≈6.07742719±.500897689i y_(3, 4) ≈3.56540959±4.08436093i z_(3, 4) ≈7.80487569±.228579540i plus all triplets with opposite signs (x_5 =−x_1 ∧y_5 =−y_1 ∧z_5 =−z_1 etc.)

lety=px∧z=qx⇒x2=9p2−p+1=30p2−pq+q2=50q2−q+1(I)(II)(III)fromI=II∧II=IIIwegetq=29p2−20p+119(p−1)insertingthisleadstop4−71391p3−240391p2+469391p−149391=0thishasno‘‘nice″solutionp1≈−1.25724339⇒q1≈−4.03560259p2≈.383450177⇒q2≈−1.36872485p3,4≈.527689447±.715546104i⇒q3,4≈1.27249620±.142489563i⇒x1≈1.53134901y1≈−1.92527842z1≈−6.17991602x2≈3.43315083y2≈1.31644230z2≈−4.69903886x3,4≈6.07742719±.500897689iy3,4≈3.56540959±4.08436093iz3,4≈7.80487569±.228579540iplusalltripletswithoppositesigns(x5=−x1∧y5=−y1∧z5=−z1etc.)

Commented by Tawa11 last updated on 12/Jun/22

Great sir.

Greatsir.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com