Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 171435 by cortano1 last updated on 15/Jun/22

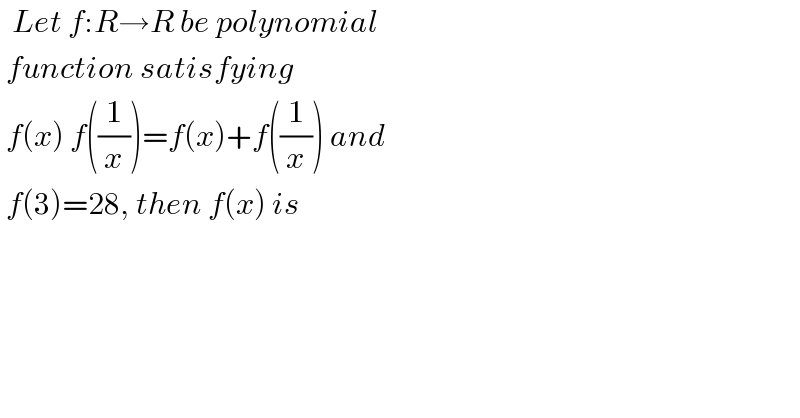
Let f:R→R be polynomial function satisfying f(x) f((1/x))=f(x)+f((1/x)) and f(3)=28, then f(x) is

$$\:\:{Let}\:{f}:{R}\rightarrow{R}\:{be}\:{polynomial} \\ $$$$\:{function}\:{satisfying}\: \\ $$$$\:{f}\left({x}\right)\:{f}\left(\frac{\mathrm{1}}{{x}}\right)={f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{{x}}\right)\:{and} \\ $$$$\:{f}\left(\mathrm{3}\right)=\mathrm{28},\:{then}\:{f}\left({x}\right)\:{is} \\ $$

Commented by infinityaction last updated on 15/Jun/22

now function is not define R→R

$${now}\:{function}\:{is}\:{not}\:{define}\:{R}\rightarrow{R} \\ $$

Commented by infinityaction last updated on 15/Jun/22

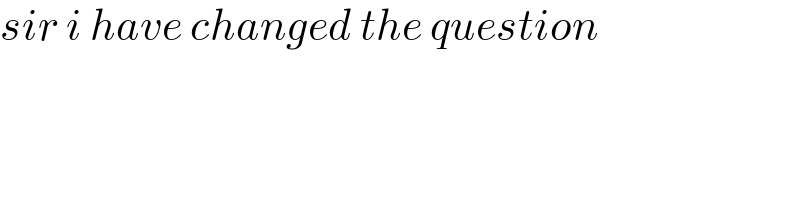
sir i have changed the question

$${sir}\:{i}\:{have}\:{changed}\:{the}\:{question} \\ $$

Commented by mr W last updated on 15/Jun/22

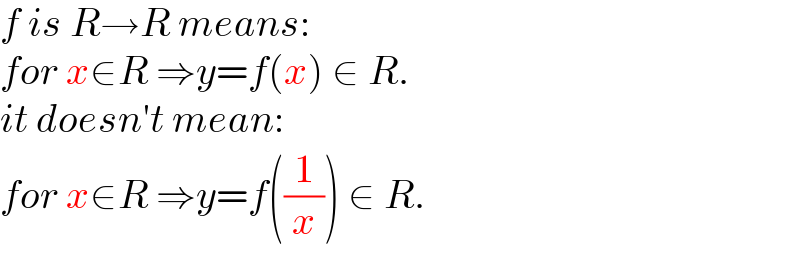
f is R→R means: for x∈R ⇒y=f(x) ∈ R. it doesn′t mean: for x∈R ⇒y=f((1/x)) ∈ R.

$${f}\:{is}\:{R}\rightarrow{R}\:{means}: \\ $$$${for}\:{x}\in{R}\:\Rightarrow{y}={f}\left({x}\right)\:\in\:{R}. \\ $$$${it}\:{doesn}'{t}\:{mean}: \\ $$$${for}\:{x}\in{R}\:\Rightarrow{y}={f}\left(\frac{\mathrm{1}}{{x}}\right)\:\in\:{R}. \\ $$

Commented by infinityaction last updated on 15/Jun/22

your question should be A polynomial function f(x) satisfying f(x) f((1/x))=f(x)+f((1/x)) and f(3)=28, then f(x) is then we know that f(x) = 1±x^n so f(3) = 1±3^n = 28 1+3^n = 28 then n= 3 f(x) = 1+x^3

$${your}\:{question}\:{should}\:{be} \\ $$$$\:\:{A}\:{polynomial}\:{function}\:{f}\left({x}\right)\:{satisfying}\: \\ $$$$\:{f}\left({x}\right)\:{f}\left(\frac{\mathrm{1}}{{x}}\right)={f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{{x}}\right)\:{and} \\ $$$$\:{f}\left(\mathrm{3}\right)=\mathrm{28},\:{then}\:{f}\left({x}\right)\:{is} \\ $$$${then}\:{we}\:{know}\:{that} \\ $$$$\:{f}\left({x}\right)\:=\:\:\mathrm{1}\pm{x}^{{n}} \\ $$$${so}\:\:{f}\left(\mathrm{3}\right)\:=\:\mathrm{1}\pm\mathrm{3}^{{n}} \:=\:\mathrm{28} \\ $$$$\:\:\:\:\:\:\mathrm{1}+\mathrm{3}^{{n}} \:=\:\mathrm{28} \\ $$$$\:\:{then}\:{n}=\:\mathrm{3} \\ $$$$\:\:\:{f}\left({x}\right)\:=\:\mathrm{1}+{x}^{\mathrm{3}} \\ $$

Commented by floor(10²Eta[1]) last updated on 15/Jun/22

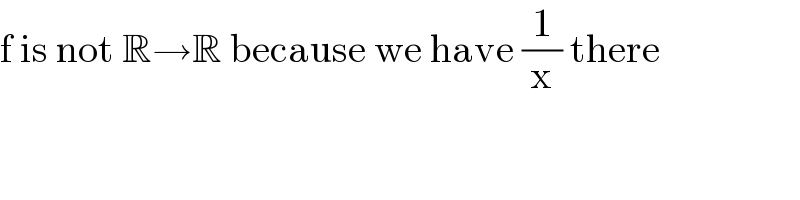
f is not R→R because we have (1/x) there

$$\mathrm{f}\:\mathrm{is}\:\mathrm{not}\:\mathbb{R}\rightarrow\mathbb{R}\:\mathrm{because}\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{there} \\ $$

Commented by floor(10²Eta[1]) last updated on 15/Jun/22

x cant be zero⇒x∉R

$$\mathrm{x}\:\mathrm{cant}\:\mathrm{be}\:\mathrm{zero}\Rightarrow\mathrm{x}\notin\mathbb{R} \\ $$

Commented by mr W last updated on 15/Jun/22

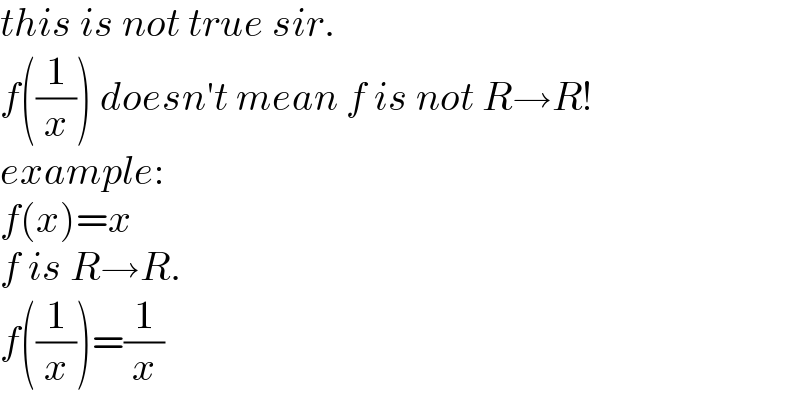
this is not true sir. f((1/x)) doesn′t mean f is not R→R! example: f(x)=x f is R→R. f((1/x))=(1/x)

$${this}\:{is}\:{not}\:{true}\:{sir}. \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)\:{doesn}'{t}\:{mean}\:{f}\:{is}\:{not}\:{R}\rightarrow{R}! \\ $$$${example}: \\ $$$${f}\left({x}\right)={x} \\ $$$${f}\:{is}\:{R}\rightarrow{R}. \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{{x}} \\ $$

Answered by aleks041103 last updated on 15/Jun/22

general solution f(x)= { ((f_1 (x),x>0)),((f_2 (x),x<0)) :} (1/(f(x))) +(1/(f(1/x)))=1 x=e^t (1/(f(e^t )))=g(t) ⇒g(t)+g(−t)=1 ⇒g(t)=(1/2)+o(t) ⇒f(x)=(1/((1/2)+o(ln(x)))) ⇒f(x)= { ((((1/2)+o_1 (ln(x)))^(−1) , x>0)),((((1/2)+o_2 (ln(−x)))^(−1) , x<0)),((f_0 , x=0)) :} where o_(1,2) (x) are odd functions, i.e. o_(1,2) (−x)=−o_(1,2) (x)

$${general}\:{solution} \\ $$$${f}\left({x}\right)=\begin{cases}{{f}_{\mathrm{1}} \left({x}\right),{x}>\mathrm{0}}\\{{f}_{\mathrm{2}} \left({x}\right),{x}<\mathrm{0}}\end{cases} \\ $$$$\frac{\mathrm{1}}{{f}\left({x}\right)}\:+\frac{\mathrm{1}}{{f}\left(\mathrm{1}/{x}\right)}=\mathrm{1} \\ $$$${x}={e}^{{t}} \\ $$$$\frac{\mathrm{1}}{{f}\left({e}^{{t}} \right)}={g}\left({t}\right) \\ $$$$\Rightarrow{g}\left({t}\right)+{g}\left(−{t}\right)=\mathrm{1} \\ $$$$\Rightarrow{g}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}+{o}\left({t}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{2}}+{o}\left({ln}\left({x}\right)\right)} \\ $$$$\Rightarrow{f}\left({x}\right)=\begin{cases}{\left(\frac{\mathrm{1}}{\mathrm{2}}+{o}_{\mathrm{1}} \left({ln}\left({x}\right)\right)\right)^{−\mathrm{1}} ,\:{x}>\mathrm{0}}\\{\left(\frac{\mathrm{1}}{\mathrm{2}}+{o}_{\mathrm{2}} \left({ln}\left(−{x}\right)\right)\right)^{−\mathrm{1}} ,\:{x}<\mathrm{0}}\\{{f}_{\mathrm{0}} \:,\:\:{x}=\mathrm{0}}\end{cases} \\ $$$${where}\:{o}_{\mathrm{1},\mathrm{2}} \left({x}\right)\:{are}\:{odd}\:{functions},\:{i}.{e}. \\ $$$${o}_{\mathrm{1},\mathrm{2}} \left(−{x}\right)=−{o}_{\mathrm{1},\mathrm{2}} \left({x}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com