
Question Number 1716 by Rasheed Soomro last updated on 02/Sep/15

$${Determine}\:{interval}\:\boldsymbol{\mathrm{A}}\:{of}\:{real}\:{numbers}\:{for}\:{which} \\ $$$${a}^{{a}+\mathrm{1}} \geqslant\left({a}+\mathrm{1}\right)^{{a}} \:\:\:\:\:\:{whenever}\:{a}\in\boldsymbol{\mathrm{A}} \\ $$
Commented by Rasheed Ahmad last updated on 03/Sep/15
![a^(a+1) ≥(a+1)^a a^a .a≥a^a (1+(1/a))^a We assume here a>0 because for a<0 a^(a+1) ,(a+1)^a may be imaginary. (At a=0 the statement is false) So a>0⇒a^a >0 a^a .a≥a^a (1+(1/a))^a ⇒(1+(1/a))^a ≤a (1+(1/a))^a ≤(a^(1/a) )^a ⇒1+(1/a)≤a^(1/a) a^(1/a) − (1/a) − 1≥ 0 a^(1/a) − (1/a) − 1=0 ∨ a^(1/a) − (1/a) − 1>0 [[With the help of graphing calculator a≥2.293....]] By using numeical methods....](Q1723.png)
$${a}^{{a}+\mathrm{1}} \geqslant\left({a}+\mathrm{1}\right)^{{a}} \\ $$$${a}^{{a}} .{a}\geqslant{a}^{{a}} \left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)^{{a}} \\ $$$${We}\:{assume}\:{here}\:{a}>\mathrm{0}\:{because} \\ $$$${for}\:{a}<\mathrm{0}\:\:\:{a}^{{a}+\mathrm{1}} ,\left({a}+\mathrm{1}\right)^{{a}} \:{may}\:{be}\: \\ $$$${imaginary}.\:\left({At}\:{a}=\mathrm{0}\:{the}\:{statement}\right. \\ $$$$\left.{is}\:{false}\right) \\ $$$${So}\:{a}>\mathrm{0}\Rightarrow{a}^{{a}} >\mathrm{0} \\ $$$${a}^{{a}} .{a}\geqslant{a}^{{a}} \left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)^{{a}} \Rightarrow\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)^{{a}} \leqslant{a} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{a}}\right)^{{a}} \leqslant\left({a}^{\frac{\mathrm{1}}{{a}}} \right)^{{a}} \\ $$$$\Rightarrow\mathrm{1}+\frac{\mathrm{1}}{{a}}\leqslant{a}^{\frac{\mathrm{1}}{{a}}} \\ $$$${a}^{\frac{\mathrm{1}}{{a}}} −\:\frac{\mathrm{1}}{{a}}\:−\:\mathrm{1}\geqslant\:\mathrm{0} \\ $$$${a}^{\frac{\mathrm{1}}{{a}}} −\:\frac{\mathrm{1}}{{a}}\:−\:\mathrm{1}=\mathrm{0}\:\vee\:{a}^{\frac{\mathrm{1}}{{a}}} −\:\frac{\mathrm{1}}{{a}}\:−\:\mathrm{1}>\mathrm{0} \\ $$$$\left[\left[{With}\:{the}\:{help}\:{of}\:{graphing}\:{calculator}\right.\right. \\ $$$$\left.{a}\left.\geqslant\mathrm{2}.\mathrm{293}....\right]\right] \\ $$$${By}\:{using}\:{numeical}\:{methods}.... \\ $$$$ \\ $$
Answered by 123456 last updated on 03/Sep/15
![x^(x+1) ≥(x+1)^x h(x)=x^(x+1) −(x+1)^x h(x)<0⇔x^(x+1) <(x+1)^x h(x)=0⇔x^(x+1) =(x+1)^x h(x)>0⇔x^(x+1) =(x+1)^x h(0)=h(1)=h(2)=−1 h(3)=17 for x∈[0,+∞) its continuous and since h(2)<0<h(3) by inthermediare value theorem (rolle theorem) ∃ξ∈[2,3],h(ξ)=0 comtinue](Q1720.png)
$${x}^{{x}+\mathrm{1}} \geqslant\left({x}+\mathrm{1}\right)^{{x}} \\ $$$${h}\left({x}\right)={x}^{{x}+\mathrm{1}} −\left({x}+\mathrm{1}\right)^{{x}} \\ $$$${h}\left({x}\right)<\mathrm{0}\Leftrightarrow{x}^{{x}+\mathrm{1}} <\left({x}+\mathrm{1}\right)^{{x}} \\ $$$${h}\left({x}\right)=\mathrm{0}\Leftrightarrow{x}^{{x}+\mathrm{1}} =\left({x}+\mathrm{1}\right)^{{x}} \\ $$$${h}\left({x}\right)>\mathrm{0}\Leftrightarrow{x}^{{x}+\mathrm{1}} =\left({x}+\mathrm{1}\right)^{{x}} \\ $$$${h}\left(\mathrm{0}\right)={h}\left(\mathrm{1}\right)={h}\left(\mathrm{2}\right)=−\mathrm{1} \\ $$$${h}\left(\mathrm{3}\right)=\mathrm{17} \\ $$$$\mathrm{for}\:{x}\in\left[\mathrm{0},+\infty\right)\:\mathrm{its}\:\mathrm{continuous}\:\mathrm{and}\:\mathrm{since} \\ $$$${h}\left(\mathrm{2}\right)<\mathrm{0}<{h}\left(\mathrm{3}\right)\:\mathrm{by}\:\mathrm{inthermediare}\:\mathrm{value}\:\mathrm{theorem}\:\left(\mathrm{rolle}\:\mathrm{theorem}\right) \\ $$$$\exists\xi\in\left[\mathrm{2},\mathrm{3}\right],{h}\left(\xi\right)=\mathrm{0} \\ $$$$\mathrm{comtinue} \\ $$
Commented by 123456 last updated on 03/Sep/15

$${h}\left({x}\right)=\mathrm{0},\:\mathrm{bissection}\:\mathrm{method}\:\left(\approx\:\mathrm{values}\right) \\ $$$$\:\:\:{a}\:\:\:\:\:\:\:\:{b}\:\:\:\:\:\:\:\:{x}\:\:\:\:\:\:{h}\left({a}\right)\:\:\:\:\:{h}\left({b}\right)\:\:\:\:\:\:\:\:{h}\left({x}\right) \\ $$$$\mathrm{2},\mathrm{00}\mid\mathrm{3},\mathrm{00}\mid\mathrm{2},\mathrm{50}\mid−\mathrm{1},\mathrm{00}\mid+\mathrm{17},\mathrm{00}\mid+\mathrm{1},\mathrm{79} \\ $$$$\mathrm{2},\mathrm{00}\mid\mathrm{2},\mathrm{50}\mid\mathrm{2},\mathrm{25}\mid−\mathrm{1},\mathrm{00}\mid+\mathrm{01},\mathrm{79}\mid−\mathrm{0},\mathrm{23} \\ $$$$\mathrm{2},\mathrm{25}\mid\mathrm{2},\mathrm{50}\mid\mathrm{2},\mathrm{38}\mid−\mathrm{0},\mathrm{23}\mid+\mathrm{01},\mathrm{79}\mid+\mathrm{0},\mathrm{59} \\ $$$$\mathrm{2},\mathrm{25}\mid\mathrm{2},\mathrm{38}\mid\mathrm{2},\mathrm{32}\mid−\mathrm{0},\mathrm{23}\mid+\mathrm{00},\mathrm{59}\mid+\mathrm{0},\mathrm{16} \\ $$$$\mathrm{2},\mathrm{25}\mid\mathrm{2},\mathrm{32}\mid\mathrm{2},\mathrm{29}\mid−\mathrm{0},\mathrm{23}\mid+\mathrm{00},\mathrm{16}\mid−\mathrm{0},\mathrm{02} \\ $$$${x}\approx\mathrm{2},\mathrm{29},\mid{h}\left({x}\right)\mid\approx\mathrm{0},\mathrm{02} \\ $$
Commented by Rasheed Ahmad last updated on 03/Sep/15
$$\mathrm{Approach}\:\mathrm{is}\:\mathrm{really}\:\mathrm{appreciable}! \\ $$
Commented by Rasheed Ahmad last updated on 14/Sep/15
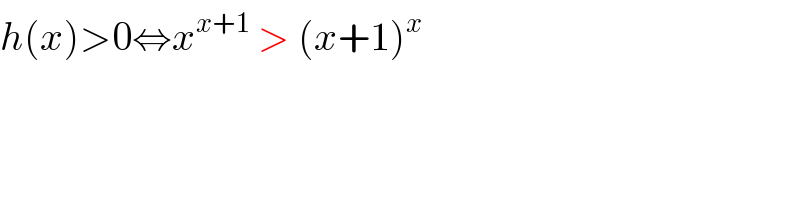
$${h}\left({x}\right)>\mathrm{0}\Leftrightarrow{x}^{{x}+\mathrm{1}} \:>\:\left({x}+\mathrm{1}\right)^{{x}} \\ $$
