
Question and Answers Forum
Question Number 171835 by Mikenice last updated on 21/Jun/22

Answered by floor(10²Eta[1]) last updated on 21/Jun/22
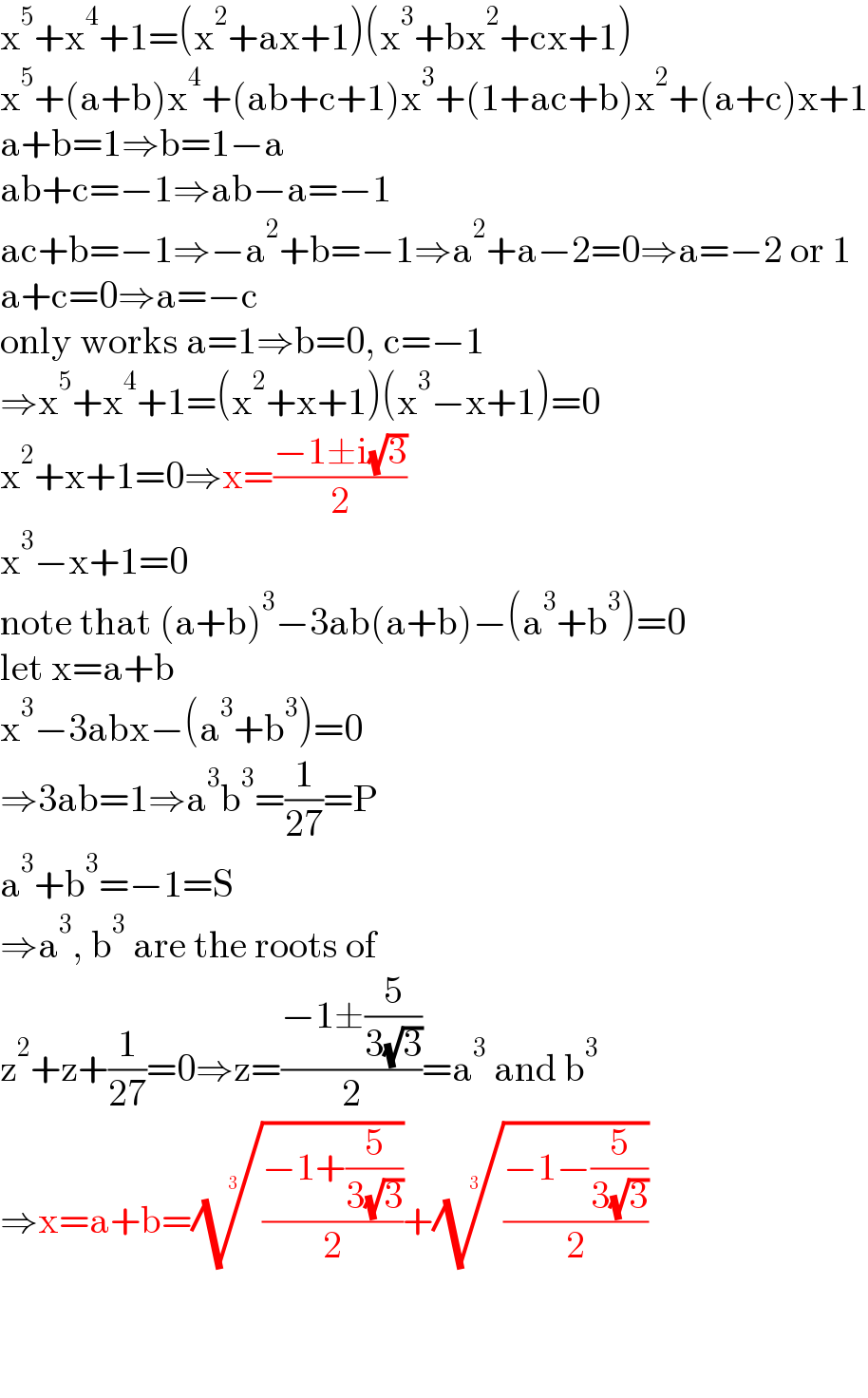
| ||
Question and Answers Forum | ||
Question Number 171835 by Mikenice last updated on 21/Jun/22 | ||
 | ||
Answered by floor(10²Eta[1]) last updated on 21/Jun/22 | ||
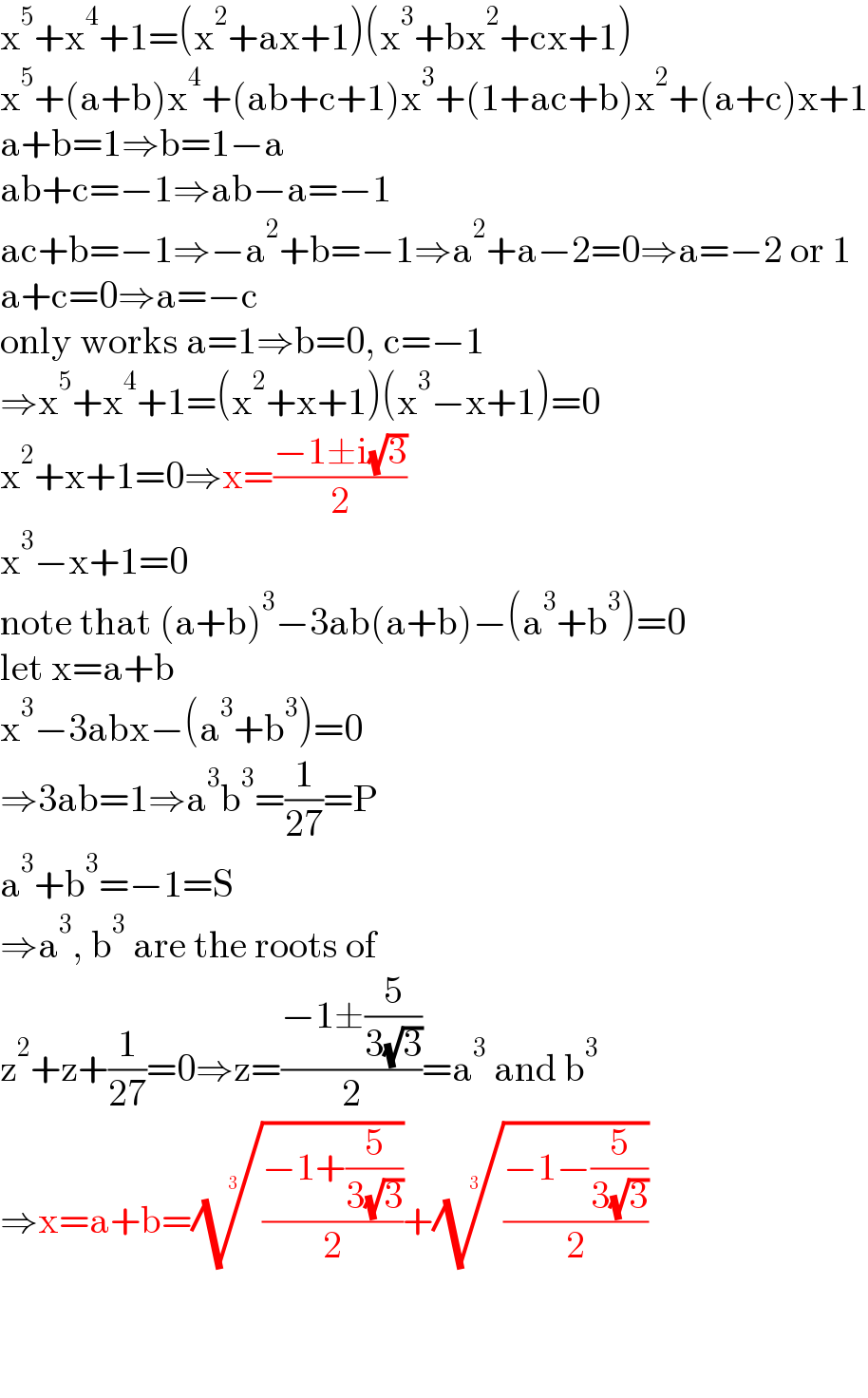 | ||
| ||