Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 171910 by Tawa11 last updated on 21/Jun/22

∫ (dx/(9 − 4x^2 )) using the trigonometric substitution.

$$\int\:\frac{\mathrm{dx}}{\mathrm{9}\:\:\:−\:\:\:\mathrm{4x}^{\mathrm{2}} } \\ $$$$\mathrm{using}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{substitution}. \\ $$

Answered by aleks041103 last updated on 21/Jun/22

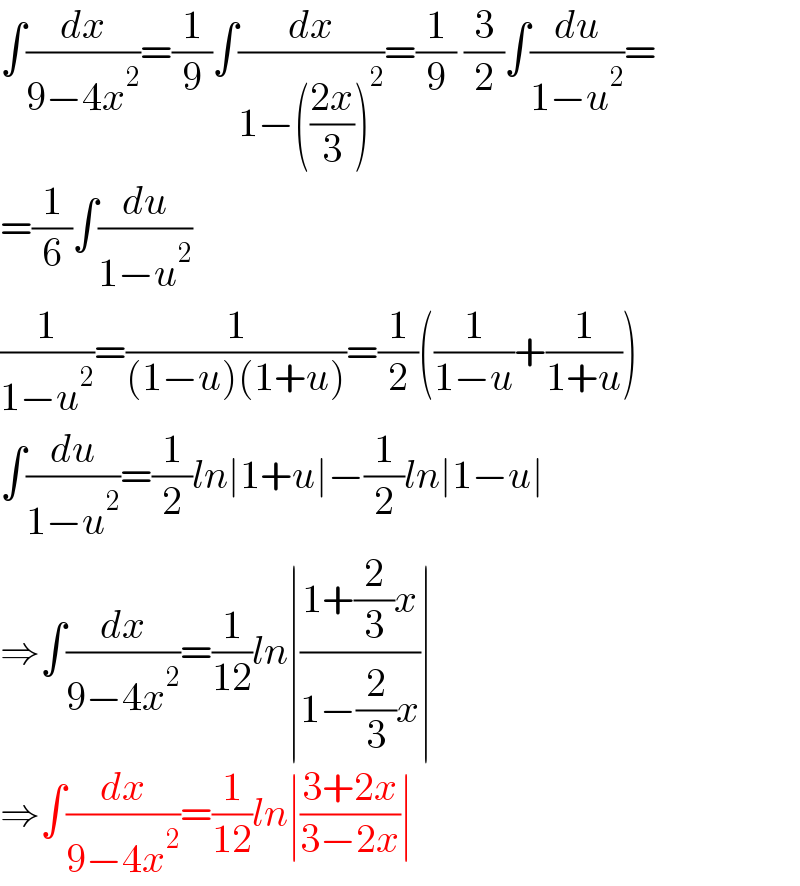
∫(dx/(9−4x^2 ))=(1/9)∫(dx/(1−(((2x)/3))^2 ))=(1/9) (3/2)∫(du/(1−u^2 ))= =(1/6)∫(du/(1−u^2 )) (1/(1−u^2 ))=(1/((1−u)(1+u)))=(1/2)((1/(1−u))+(1/(1+u))) ∫(du/(1−u^2 ))=(1/2)ln∣1+u∣−(1/2)ln∣1−u∣ ⇒∫(dx/(9−4x^2 ))=(1/(12))ln∣((1+(2/3)x)/(1−(2/3)x))∣ ⇒∫(dx/(9−4x^2 ))=(1/(12))ln∣((3+2x)/(3−2x))∣

$$\int\frac{{dx}}{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{dx}}{\mathrm{1}−\left(\frac{\mathrm{2}{x}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{9}}\:\frac{\mathrm{3}}{\mathrm{2}}\int\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{2}} }=\frac{\mathrm{1}}{\left(\mathrm{1}−{u}\right)\left(\mathrm{1}+{u}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right) \\ $$$$\int\frac{{du}}{\mathrm{1}−{u}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}+{u}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}−{u}\mid \\ $$$$\Rightarrow\int\frac{{dx}}{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{12}}{ln}\mid\frac{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}{x}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}{x}}\mid \\ $$$$\Rightarrow\int\frac{{dx}}{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{12}}{ln}\mid\frac{\mathrm{3}+\mathrm{2}{x}}{\mathrm{3}−\mathrm{2}{x}}\mid \\ $$

Commented by Tawa11 last updated on 21/Jun/22

I appreciate sir.

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 21/Jun/22

But sir, I need the trigonometric[substion. like. let x = 3 tanθ

$$\mathrm{But}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{need}\:\mathrm{the}\:\mathrm{trigonometric}\left[\mathrm{substion}.\right. \\ $$$$\mathrm{like}.\:\:\:\mathrm{let}\:\:\mathrm{x}\:\:=\:\:\mathrm{3}\:\mathrm{tan}\theta \\ $$

Commented by Tawa11 last updated on 21/Jun/22

Can the question be solved using trigonometric substitution?

$$\mathrm{Can}\:\mathrm{the}\:\mathrm{question}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{trigonometric}\:\mathrm{substitution}? \\ $$

Commented by mr W last updated on 21/Jun/22

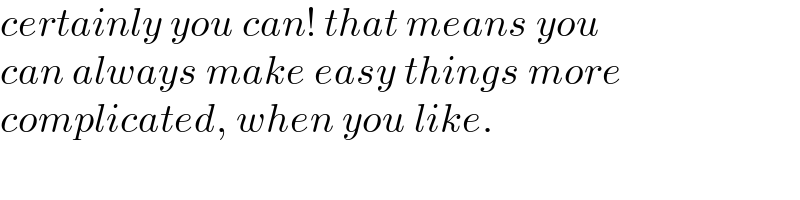
certainly you can! that means you can always make easy things more complicated, when you like.

$${certainly}\:{you}\:{can}!\:{that}\:{means}\:{you} \\ $$$${can}\:{always}\:{make}\:{easy}\:{things}\:{more} \\ $$$${complicated},\:{when}\:{you}\:{like}. \\ $$

Commented by Tawa11 last updated on 21/Jun/22

Because the condition given is using trigonometric substitution sir.

$$\mathrm{Because}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{given}\:\mathrm{is}\:\mathrm{using}\:\mathrm{trigonometric}\:\mathrm{substitution}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 21/Jun/22

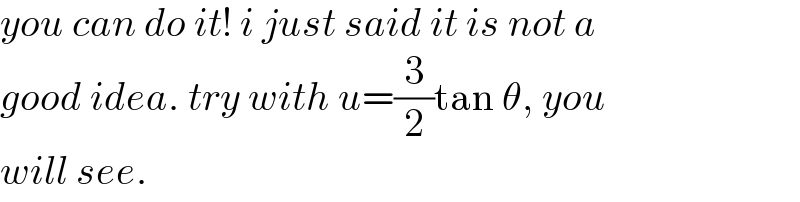
you can do it! i just said it is not a good idea. try with u=(3/2)tan θ, you will see.

$${you}\:{can}\:{do}\:{it}!\:{i}\:{just}\:{said}\:{it}\:{is}\:{not}\:{a} \\ $$$${good}\:{idea}.\:{try}\:{with}\:{u}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{tan}\:\theta,\:{you} \\ $$$${will}\:{see}. \\ $$

Commented by Tawa11 last updated on 21/Jun/22

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by Tawa11 last updated on 22/Jun/22

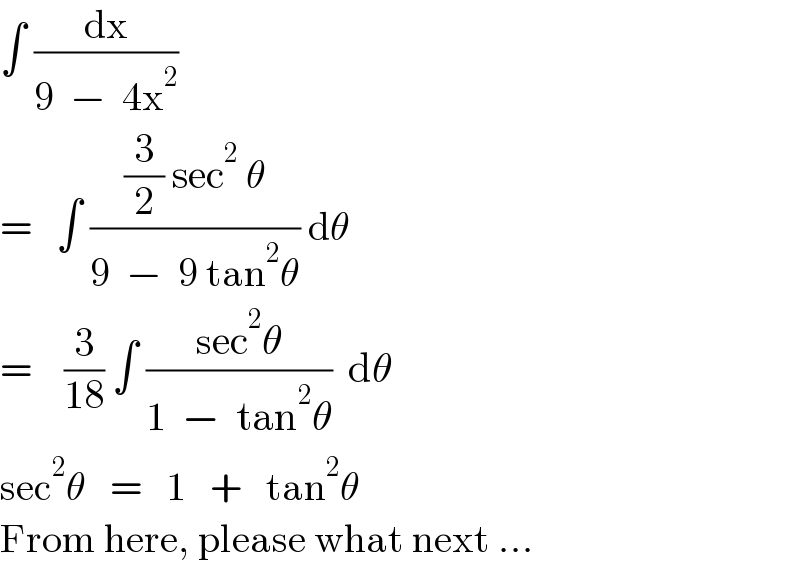
∫ (dx/(9 − 4x^2 )) = ∫ (((3/2) sec^2 θ)/(9 − 9 tan^2 θ)) dθ = (3/(18)) ∫ ((sec^2 θ)/(1 − tan^2 θ)) dθ sec^2 θ = 1 + tan^2 θ From here, please what next ...

$$\int\:\frac{\mathrm{dx}}{\mathrm{9}\:\:−\:\:\mathrm{4x}^{\mathrm{2}} } \\ $$$$=\:\:\:\int\:\frac{\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{sec}^{\mathrm{2}} \:\theta}{\mathrm{9}\:\:−\:\:\mathrm{9}\:\mathrm{tan}^{\mathrm{2}} \theta}\:\mathrm{d}\theta \\ $$$$=\:\:\:\:\frac{\mathrm{3}}{\mathrm{18}}\:\int\:\frac{\mathrm{sec}^{\mathrm{2}} \theta}{\mathrm{1}\:\:−\:\:\mathrm{tan}^{\mathrm{2}} \theta}\:\:\mathrm{d}\theta \\ $$$$\mathrm{sec}^{\mathrm{2}} \theta\:\:\:=\:\:\:\mathrm{1}\:\:\:+\:\:\:\mathrm{tan}^{\mathrm{2}} \theta\:\:\:\:\:\:\: \\ $$$$\mathrm{From}\:\mathrm{here},\:\mathrm{please}\:\mathrm{what}\:\mathrm{next}\:... \\ $$

Answered by ajfour last updated on 22/Jun/22

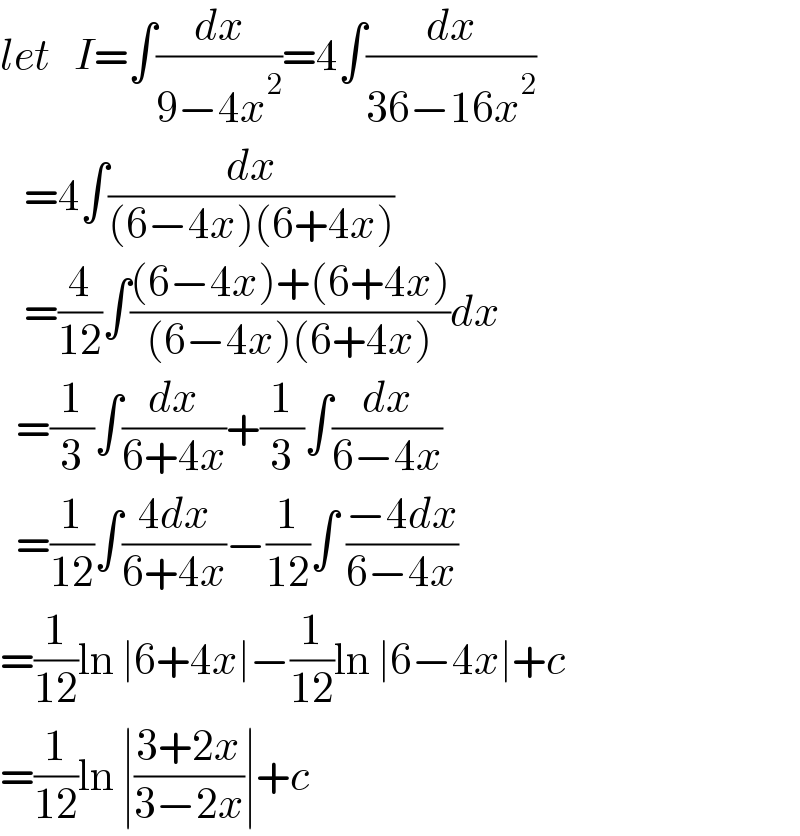
let I=∫(dx/(9−4x^2 ))=4∫(dx/(36−16x^2 )) =4∫(dx/((6−4x)(6+4x))) =(4/(12))∫(((6−4x)+(6+4x))/((6−4x)(6+4x)))dx =(1/3)∫(dx/(6+4x))+(1/3)∫(dx/(6−4x)) =(1/(12))∫((4dx)/(6+4x))−(1/(12))∫ ((−4dx)/(6−4x)) =(1/(12))ln ∣6+4x∣−(1/(12))ln ∣6−4x∣+c =(1/(12))ln ∣((3+2x)/(3−2x))∣+c

$${let}\:\:\:{I}=\int\frac{{dx}}{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }=\mathrm{4}\int\frac{{dx}}{\mathrm{36}−\mathrm{16}{x}^{\mathrm{2}} } \\ $$$$\:\:\:=\mathrm{4}\int\frac{{dx}}{\left(\mathrm{6}−\mathrm{4}{x}\right)\left(\mathrm{6}+\mathrm{4}{x}\right)} \\ $$$$\:\:\:=\frac{\mathrm{4}}{\mathrm{12}}\int\frac{\left(\mathrm{6}−\mathrm{4}{x}\right)+\left(\mathrm{6}+\mathrm{4}{x}\right)}{\left(\mathrm{6}−\mathrm{4}{x}\right)\left(\mathrm{6}+\mathrm{4}{x}\right)}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{6}+\mathrm{4}{x}}+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{6}−\mathrm{4}{x}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{12}}\int\frac{\mathrm{4}{dx}}{\mathrm{6}+\mathrm{4}{x}}−\frac{\mathrm{1}}{\mathrm{12}}\int\:\frac{−\mathrm{4}{dx}}{\mathrm{6}−\mathrm{4}{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\:\mid\mathrm{6}+\mathrm{4}{x}\mid−\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\:\mid\mathrm{6}−\mathrm{4}{x}\mid+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\:\mid\frac{\mathrm{3}+\mathrm{2}{x}}{\mathrm{3}−\mathrm{2}{x}}\mid+{c} \\ $$

Commented by Tawa11 last updated on 22/Jun/22

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Answered by thfchristopher last updated on 22/Jun/22

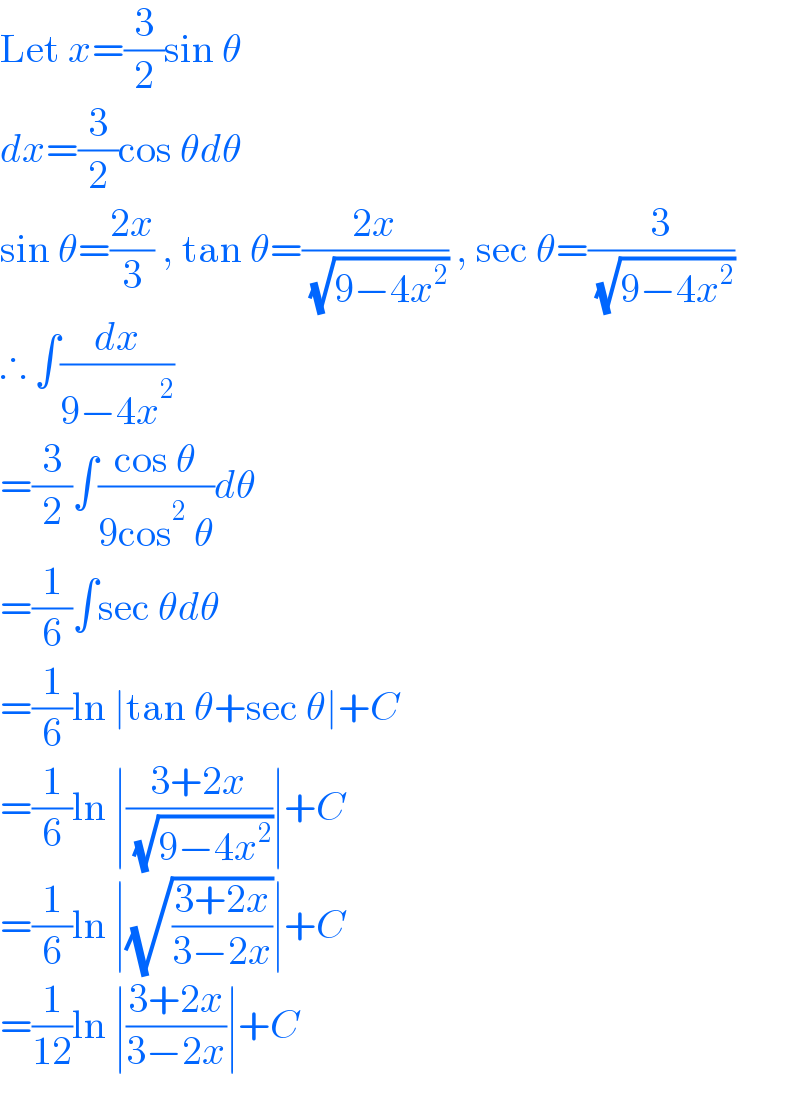
Let x=(3/2)sin θ dx=(3/2)cos θdθ sin θ=((2x)/3) , tan θ=((2x)/( (√(9−4x^2 )))) , sec θ=(3/( (√(9−4x^2 )))) ∴ ∫(dx/(9−4x^2 )) =(3/2)∫((cos θ)/(9cos^2 θ))dθ =(1/6)∫sec θdθ =(1/6)ln ∣tan θ+sec θ∣+C =(1/6)ln ∣((3+2x)/( (√(9−4x^2 ))))∣+C =(1/6)ln ∣(√((3+2x)/(3−2x)))∣+C =(1/(12))ln ∣((3+2x)/(3−2x))∣+C

$$\mathrm{Let}\:{x}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{sin}\:\theta \\ $$$${dx}=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\:\theta{d}\theta \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{2}{x}}{\mathrm{3}}\:,\:\mathrm{tan}\:\theta=\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }}\:,\:\mathrm{sec}\:\theta=\frac{\mathrm{3}}{\:\sqrt{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }} \\ $$$$\therefore\:\int\frac{{dx}}{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{cos}\:\theta}{\mathrm{9cos}^{\mathrm{2}} \:\theta}{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int\mathrm{sec}\:\theta{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\mid\mathrm{tan}\:\theta+\mathrm{sec}\:\theta\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\mid\frac{\mathrm{3}+\mathrm{2}{x}}{\:\sqrt{\mathrm{9}−\mathrm{4}{x}^{\mathrm{2}} }}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\mid\sqrt{\frac{\mathrm{3}+\mathrm{2}{x}}{\mathrm{3}−\mathrm{2}{x}}}\mid+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\mathrm{ln}\:\mid\frac{\mathrm{3}+\mathrm{2}{x}}{\mathrm{3}−\mathrm{2}{x}}\mid+{C} \\ $$

Commented by thfchristopher last updated on 22/Jun/22

Trigonometric substitution applied on integral format: (i)∫(dx/(a^2 +b^2 x^2 )) or ∫(dx/(b^2 x^2 +a^2 )) Let bx=atan θ (ii) ∫(dx/(a^2 −b^2 x^2 )) Let bx=asin θ (iii) ∫(dx/(b^2 x^2 −a^2 )) Let bx=asec θ

$$\mathrm{Trigonometric}\:\mathrm{substitution}\:\mathrm{applied}\:\mathrm{on}\: \\ $$$$\mathrm{integral}\:\mathrm{format}: \\ $$$$\left(\mathrm{i}\right)\int\frac{{dx}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}^{\mathrm{2}} }\:\:\mathrm{or}\:\int\frac{{dx}}{{b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$$$\mathrm{Let}\:{bx}={a}\mathrm{tan}\:\theta \\ $$$$\left(\mathrm{ii}\right)\:\int\frac{{dx}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$$\mathrm{Let}\:{bx}={a}\mathrm{sin}\:\theta \\ $$$$\left(\mathrm{iii}\right)\:\int\frac{{dx}}{{b}^{\mathrm{2}} {x}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\mathrm{Let}\:{bx}={a}\mathrm{sec}\:\theta \\ $$

Commented by Tawa11 last updated on 22/Jun/22

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by Tawa11 last updated on 22/Jun/22

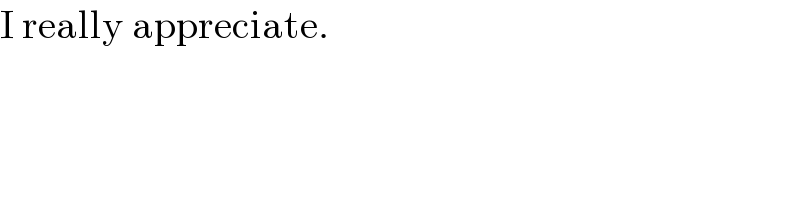
I really appreciate.

$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Commented by mr W last updated on 22/Jun/22

a substitution doesn′t make the thing easier in any form, therefore unnecesary. e.g. ∫(dx/(a^2 −b^2 x^2 )) =(1/(2a))∫((1/(a−bx))+(1/(a+bx)))dx =(1/(2ab))[−ln (a−bx)+ln (a+bx)] =(1/(2ab))×ln ∣((a+bx)/(a−bx))∣+C ∫(dx/(b^2 x^2 −a^2 ))=−∫(dx/(a^2 −b^2 x^2 ))=−(1/(2ab))×ln ∣((a+bx)/(a−bx))∣+C

$${a}\:{substitution}\:{doesn}'{t}\:{make}\:{the}\:{thing} \\ $$$${easier}\:{in}\:{any}\:{form},\:{therefore}\:{unnecesary}. \\ $$$${e}.{g}. \\ $$$$\int\frac{{dx}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}\int\left(\frac{\mathrm{1}}{{a}−{bx}}+\frac{\mathrm{1}}{{a}+{bx}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ab}}\left[−\mathrm{ln}\:\left({a}−{bx}\right)+\mathrm{ln}\:\left({a}+{bx}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ab}}×\mathrm{ln}\:\mid\frac{{a}+{bx}}{{a}−{bx}}\mid+{C} \\ $$$$\int\frac{{dx}}{{b}^{\mathrm{2}} {x}^{\mathrm{2}} −{a}^{\mathrm{2}} }=−\int\frac{{dx}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} {x}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}{ab}}×\mathrm{ln}\:\mid\frac{{a}+{bx}}{{a}−{bx}}\mid+{C} \\ $$

Commented by Tawa11 last updated on 22/Jun/22

God bless you sir. I really appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com