
Question and Answers Forum
Question Number 17206 by Arnab Maiti last updated on 02/Jul/17
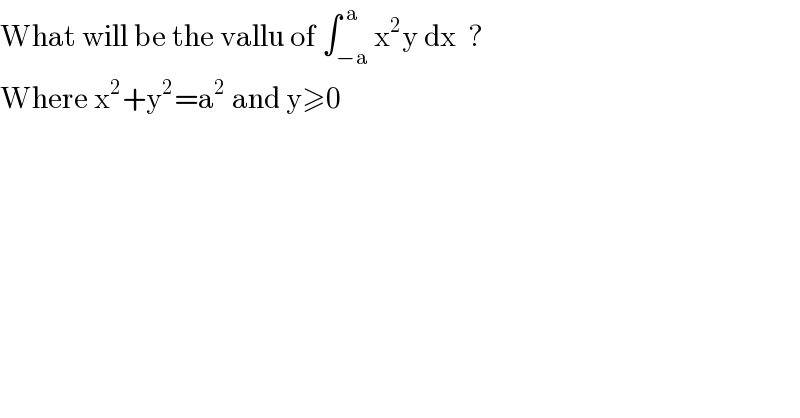
Answered by mrW1 last updated on 02/Jul/17
![let x=a cos θ and y=a sin θ dx=−asin θ dθ x∈[−a,a] and y≥0 ≡θ∈[π,0] ∫_(−a) ^a x^2 ydx=∫_π ^0 a^2 cos^2 θ a sin θ (−asin θ)dθ =−a^4 ∫_π ^0 cos^2 θ sin^2 θ dθ =a^4 ∫_0 ^π cos^2 θ sin^2 θ dθ =(a^4 /4) ∫_0 ^π (2cos θ sin θ)^2 dθ =(a^4 /4) ∫_0 ^π sin^2 2θ dθ =(a^4 /8) ∫_0 ^π [1−cos 4θ ] dθ =(a^4 /8) [θ−(1/4)sin 4θ ]_0 ^π =(a^4 /8)×π =((πa^4 )/8)](Q17214.png)
Commented by Arnab Maiti last updated on 02/Jul/17

| ||
Question and Answers Forum | ||
Question Number 17206 by Arnab Maiti last updated on 02/Jul/17 | ||
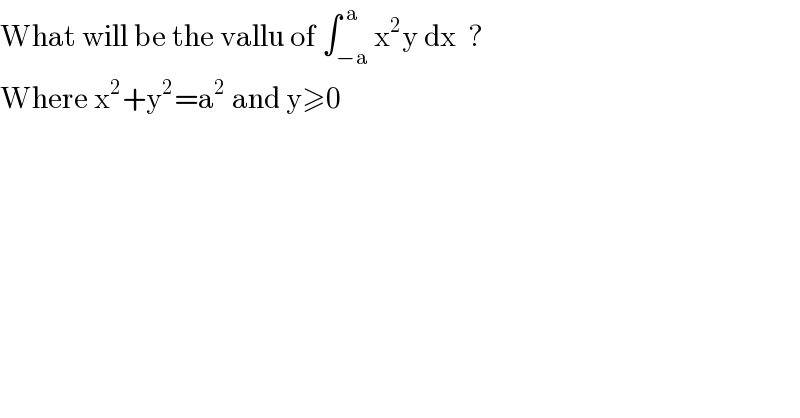 | ||
Answered by mrW1 last updated on 02/Jul/17 | ||
![let x=a cos θ and y=a sin θ dx=−asin θ dθ x∈[−a,a] and y≥0 ≡θ∈[π,0] ∫_(−a) ^a x^2 ydx=∫_π ^0 a^2 cos^2 θ a sin θ (−asin θ)dθ =−a^4 ∫_π ^0 cos^2 θ sin^2 θ dθ =a^4 ∫_0 ^π cos^2 θ sin^2 θ dθ =(a^4 /4) ∫_0 ^π (2cos θ sin θ)^2 dθ =(a^4 /4) ∫_0 ^π sin^2 2θ dθ =(a^4 /8) ∫_0 ^π [1−cos 4θ ] dθ =(a^4 /8) [θ−(1/4)sin 4θ ]_0 ^π =(a^4 /8)×π =((πa^4 )/8)](Q17214.png) | ||
| ||
Commented by Arnab Maiti last updated on 02/Jul/17 | ||
 | ||