Question Number 172234 by Sotoberry last updated on 24/Jun/22
Commented by cortano1 last updated on 24/Jun/22
![S = ∫_0 ^( 2π) (√(((dx/dθ))^2 +((dy/dθ))^2 )) dθ { (((dx/dθ) = −3acos^2 θ sin θ )),(((dy/dθ)= 2asin θ cos θ)) :} S=∫_0 ^(2π) (√(9a^2 sin^2 θ cos^4 θ+4a^2 sin^2 θ cos^2 θ)) dθ = ∫_0 ^(2π) ∣a∣sin θ cos θ (√(9 cos^2 θ+4)) dθ = −((4∣a∣)/(18)) ∫_0 ^(π/2) (√(9cos^2 θ+4)) d(9cos^2 θ+4) =−((2∣a∣)/9).(2/3) [ 9cos^2 θ+4 ]_0 ^(π/2) =−((4∣a∣)/(27)) [ 4−13 ] = ((4∣a∣)/3)](Q172238.png)
$$\:{S}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \sqrt{\left(\frac{{dx}}{{d}\theta}\right)^{\mathrm{2}} +\left(\frac{{dy}}{{d}\theta}\right)^{\mathrm{2}} }\:{d}\theta \\ $$$$\:\begin{cases}{\frac{{dx}}{{d}\theta}\:=\:−\mathrm{3}{a}\mathrm{cos}\:^{\mathrm{2}} \theta\:\mathrm{sin}\:\theta\:}\\{\frac{{dy}}{{d}\theta}=\:\mathrm{2}{a}\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta}\end{cases} \\ $$$$\:{S}=\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\:\sqrt{\mathrm{9}{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:^{\mathrm{4}} \theta+\mathrm{4}{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta\:\mathrm{cos}\:^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$\:=\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\mid{a}\mid\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\sqrt{\mathrm{9}\:\mathrm{cos}\:^{\mathrm{2}} \theta+\mathrm{4}}\:{d}\theta \\ $$$$=\:−\frac{\mathrm{4}\mid{a}\mid}{\mathrm{18}}\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\sqrt{\mathrm{9cos}\:^{\mathrm{2}} \theta+\mathrm{4}}\:{d}\left(\mathrm{9cos}\:^{\mathrm{2}} \theta+\mathrm{4}\right) \\ $$$$=−\frac{\mathrm{2}\mid{a}\mid}{\mathrm{9}}.\frac{\mathrm{2}}{\mathrm{3}}\:\left[\:\mathrm{9cos}\:^{\mathrm{2}} \theta+\mathrm{4}\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{4}\mid{a}\mid}{\mathrm{27}}\:\left[\:\mathrm{4}−\mathrm{13}\:\right]\:=\:\frac{\mathrm{4}\mid{a}\mid}{\mathrm{3}}\: \\ $$
Answered by mr W last updated on 24/Jun/22
![(dx/dθ)=−3a cos^2 θ sin θ (dy/dθ)=2a sin θ cos θ ds=(√((dx)^2 +(dy)^2 )) =(√(a^2 sin^2 θ cos^2 θ (9 cos^2 θ+4))) dθ =(a/(2(√2))) ∣sin 2θ∣(√(9 cos 2θ+17)) dθ the curve from θ=π to 2π is the same as from θ=0 to π, therefore i just calculate the length from θ=0 to π. s=∫_0 ^π ds =2∫_0 ^(π/2) ds =((2a)/(2(√2)))∫_0 ^(π/2) sin 2θ (√(9 cos 2θ+17)) dθ =(a/( 18(√2)))∫_(π/2) ^0 (√(9 cos 2θ+17)) d(9 cos 2θ+17) =(a/( 18(√2)))×(2/3)[(9 cos 2θ+17)^(3/2) ]_(π/2) ^0 =(a/( 27(√2)))[(9+17)^(3/2) −(−9+17)^(3/2) ] =(a/( 27(√2)))×(26^(3/2) −8^(3/2) ) =(a/( 27(√2)))×(26(√(26))−16(√2)) =((2(13(√(13))−8)a)/( 27)) ≈2.879 a](Q172241.png)
$$\frac{{dx}}{{d}\theta}=−\mathrm{3}{a}\:\mathrm{cos}^{\mathrm{2}} \:\theta\:\mathrm{sin}\:\theta \\ $$$$\frac{{dy}}{{d}\theta}=\mathrm{2}{a}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$${ds}=\sqrt{\left({dx}\right)^{\mathrm{2}} +\left({dy}\right)^{\mathrm{2}} } \\ $$$$=\sqrt{{a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{cos}^{\mathrm{2}} \:\theta\:\left(\mathrm{9}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{4}\right)}\:{d}\theta \\ $$$$=\frac{{a}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mid\mathrm{sin}\:\mathrm{2}\theta\mid\sqrt{\mathrm{9}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{17}}\:{d}\theta \\ $$$$ \\ $$$${the}\:{curve}\:{from}\:\theta=\pi\:{to}\:\mathrm{2}\pi\:{is}\:{the} \\ $$$${same}\:{as}\:{from}\:\theta=\mathrm{0}\:{to}\:\pi,\:{therefore} \\ $$$${i}\:{just}\:{calculate}\:{the}\:{length}\:{from} \\ $$$$\theta=\mathrm{0}\:{to}\:\pi. \\ $$$${s}=\int_{\mathrm{0}} ^{\pi} {ds} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ds} \\ $$$$=\frac{\mathrm{2}{a}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}\:\mathrm{2}\theta\:\sqrt{\mathrm{9}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{17}}\:{d}\theta \\ $$$$=\frac{{a}}{\:\mathrm{18}\sqrt{\mathrm{2}}}\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \sqrt{\mathrm{9}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{17}}\:{d}\left(\mathrm{9}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{17}\right) \\ $$$$=\frac{{a}}{\:\mathrm{18}\sqrt{\mathrm{2}}}×\frac{\mathrm{2}}{\mathrm{3}}\left[\left(\mathrm{9}\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{17}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \\ $$$$=\frac{{a}}{\:\mathrm{27}\sqrt{\mathrm{2}}}\left[\left(\mathrm{9}+\mathrm{17}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(−\mathrm{9}+\mathrm{17}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right] \\ $$$$=\frac{{a}}{\:\mathrm{27}\sqrt{\mathrm{2}}}×\left(\mathrm{26}^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{8}^{\frac{\mathrm{3}}{\mathrm{2}}} \right) \\ $$$$=\frac{{a}}{\:\mathrm{27}\sqrt{\mathrm{2}}}×\left(\mathrm{26}\sqrt{\mathrm{26}}−\mathrm{16}\sqrt{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{2}\left(\mathrm{13}\sqrt{\mathrm{13}}−\mathrm{8}\right){a}}{\:\mathrm{27}} \\ $$$$\approx\mathrm{2}.\mathrm{879}\:{a} \\ $$
Commented by mr W last updated on 24/Jun/22
Commented by mr W last updated on 25/Jun/22
$${length}\:{should}\:{be}\:>\mathrm{2}\sqrt{\mathrm{2}}{a}=\mathrm{2}.\mathrm{83}{a} \\ $$$${s}=\mathrm{2}.\mathrm{879}{a}\:{seems}\:{to}\:{be}\:{correct}. \\ $$
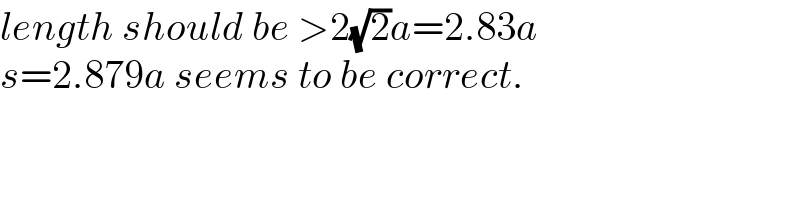
Commented by Tawa11 last updated on 25/Jun/22
$$\mathrm{Great}\:\mathrm{sir} \\ $$