
Question and Answers Forum
Question Number 172306 by mathocean1 last updated on 25/Jun/22
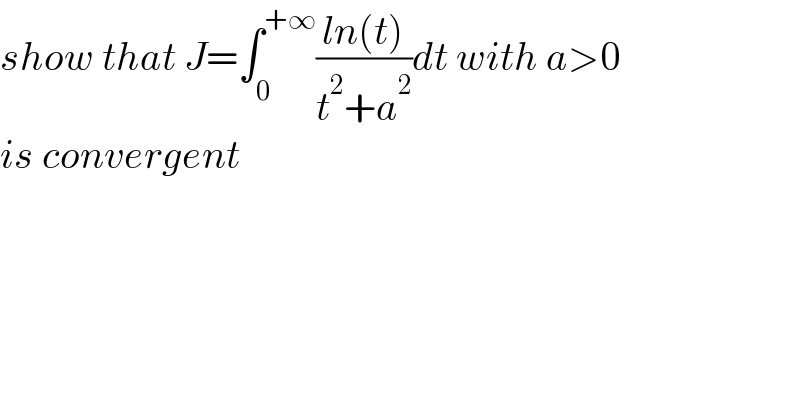
Answered by aleks041103 last updated on 25/Jun/22
![(1/a^2 )∫_0 ^∞ ((ln(t)dt)/((t/a)^2 +1))=(1/a^2 )∫_0 ^∞ ((ln(ax)d(ax))/(x^2 +1))= =(1/a)[∫_0 ^∞ ((ln(x)dx)/(1+x^2 ))+ln(a)∫_0 ^∞ (dx/(1+x^2 ))]= =((πln(a))/(2a))+(1/a)∫_0 ^∞ ((ln(x)dx)/(1+x^2 ))= =((πln(a))/(2a))+(1/a)I I=∫_0 ^∞ ((ln(x)dx)/(1+x^2 ))=∫_0 ^∞ ((ln(x))/(1+(1/x)^2 )) (dx/x^2 )= =∫_0 ^∞ ((−ln(1/x))/(1+(1/x)^2 ))d(−1/x)=∫_∞ ^0 ((ln(u)du)/(1+u^2 ))=−I ⇒I=−I⇒I=0 ⇒J(a)=((πln(a))/(2a)) This is obviously finite for a>0.](Q172320.png)
Answered by Mathspace last updated on 25/Jun/22

| ||
Question and Answers Forum | ||
Question Number 172306 by mathocean1 last updated on 25/Jun/22 | ||
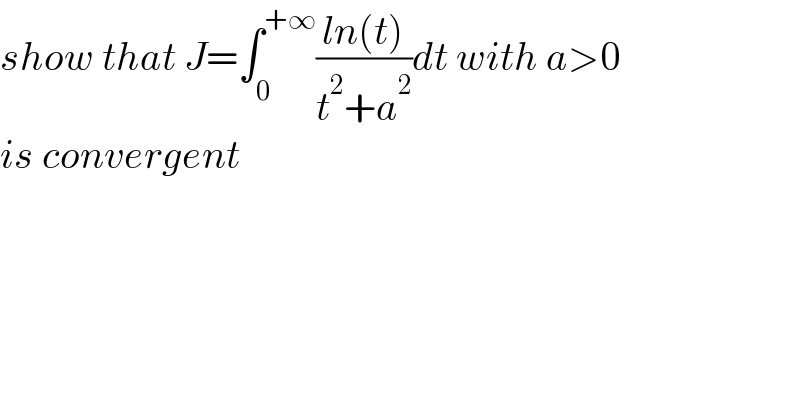 | ||
Answered by aleks041103 last updated on 25/Jun/22 | ||
![(1/a^2 )∫_0 ^∞ ((ln(t)dt)/((t/a)^2 +1))=(1/a^2 )∫_0 ^∞ ((ln(ax)d(ax))/(x^2 +1))= =(1/a)[∫_0 ^∞ ((ln(x)dx)/(1+x^2 ))+ln(a)∫_0 ^∞ (dx/(1+x^2 ))]= =((πln(a))/(2a))+(1/a)∫_0 ^∞ ((ln(x)dx)/(1+x^2 ))= =((πln(a))/(2a))+(1/a)I I=∫_0 ^∞ ((ln(x)dx)/(1+x^2 ))=∫_0 ^∞ ((ln(x))/(1+(1/x)^2 )) (dx/x^2 )= =∫_0 ^∞ ((−ln(1/x))/(1+(1/x)^2 ))d(−1/x)=∫_∞ ^0 ((ln(u)du)/(1+u^2 ))=−I ⇒I=−I⇒I=0 ⇒J(a)=((πln(a))/(2a)) This is obviously finite for a>0.](Q172320.png) | ||
| ||
Answered by Mathspace last updated on 25/Jun/22 | ||
 | ||
| ||