
Question and Answers Forum
Question Number 172307 by mathocean1 last updated on 25/Jun/22
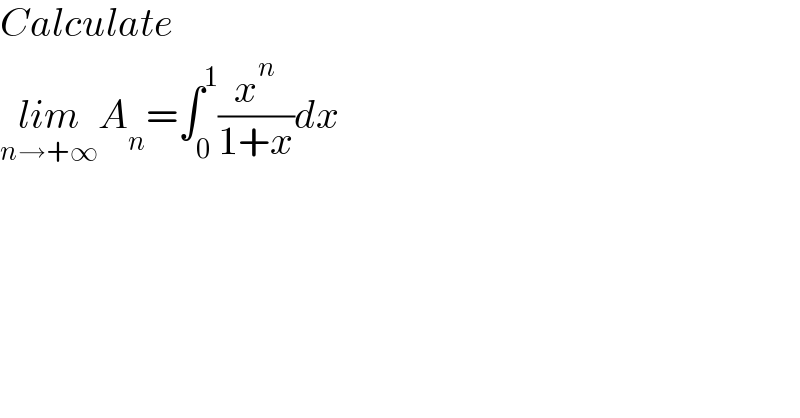
Answered by aleks041103 last updated on 25/Jun/22
![A_n =∫_0 ^1 (x^n /(1−(−x)))dx=(−1)^n ∫_0 ^1 (((−x)^n −1+1)/(1−(−x)))dx= =(−1)^(n+1) ∫_0 ^1 ((1−(−x)^n −1)/(1−(−x)))dx= =(−1)^(n+1) [∫_0 ^1 ((1−(−x)^n )/(1−(−x)))dx−∫_0 ^1 (dx/(1+x))]= =(−1)^(n+1) [∫_0 ^1 (Σ_(k=1) ^n (−x)^(k−1) )dx−ln(1+1)+ln(1+0)]= =(−1)^(n+1) [Σ_(k=1) ^n (−1)^(k−1) (∫_0 ^1 x^(k−1) dx)−ln(2)]= =(−1)^(n+1) [Σ_(k=1) ^n (((−1)^(k−1) )/k)−ln(2)] (1/(1+x))=Σ_(k=0) ^∞ (−x)^k ⇒∫_0 ^s (dx/(1+x))=ln(1+s)=Σ_(k=0) ^∞ (−1)^k (s^(k+1) /(k+1))= ⇒ln(1+s)=Σ_(k=1) ^∞ (((−1)^(k−1) s^k )/k) ⇒Σ_(k=1) ^n (((−1)^(k−1) )/k)=ln(2)−Σ_(k=n+1) ^∞ (((−1)^(k−1) )/k) ⇒A_n =(−1)^n Σ_(k=n+1) ^∞ (((−1)^(k−1) )/k) ⇒lim_(n→∞) A_n =0](Q172318.png)
Answered by Mathspace last updated on 25/Jun/22
![A_n =∫_R^+ (x^n /(1+x))χ_([0,1]) (x)dx =∫_R^+ f_n (x)dx f_m converge simplement vers0 car x ∈[0,1] and f_n est dominee par g(x)=(1/(1+x)) ⇒lim A_n =∫_R^+ lim f_n =0](Q172330.png)
Answered by puissant last updated on 25/Jun/22
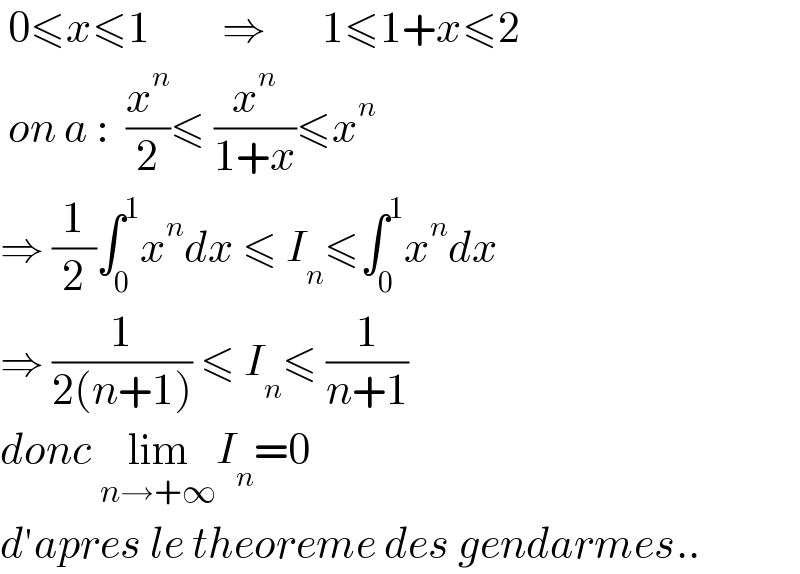
| ||
Question and Answers Forum | ||
Question Number 172307 by mathocean1 last updated on 25/Jun/22 | ||
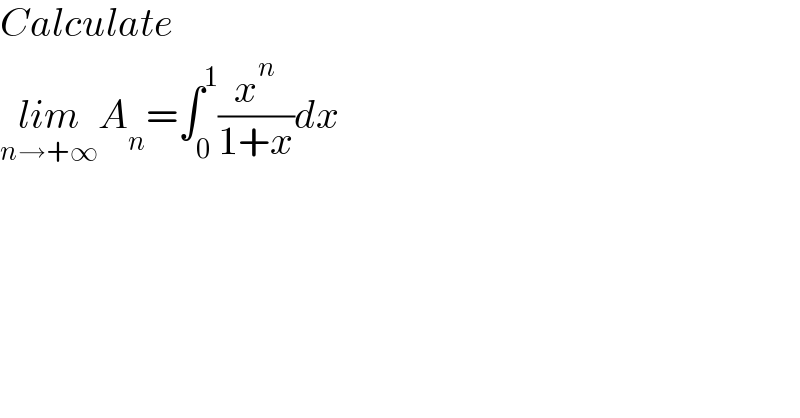 | ||
Answered by aleks041103 last updated on 25/Jun/22 | ||
![A_n =∫_0 ^1 (x^n /(1−(−x)))dx=(−1)^n ∫_0 ^1 (((−x)^n −1+1)/(1−(−x)))dx= =(−1)^(n+1) ∫_0 ^1 ((1−(−x)^n −1)/(1−(−x)))dx= =(−1)^(n+1) [∫_0 ^1 ((1−(−x)^n )/(1−(−x)))dx−∫_0 ^1 (dx/(1+x))]= =(−1)^(n+1) [∫_0 ^1 (Σ_(k=1) ^n (−x)^(k−1) )dx−ln(1+1)+ln(1+0)]= =(−1)^(n+1) [Σ_(k=1) ^n (−1)^(k−1) (∫_0 ^1 x^(k−1) dx)−ln(2)]= =(−1)^(n+1) [Σ_(k=1) ^n (((−1)^(k−1) )/k)−ln(2)] (1/(1+x))=Σ_(k=0) ^∞ (−x)^k ⇒∫_0 ^s (dx/(1+x))=ln(1+s)=Σ_(k=0) ^∞ (−1)^k (s^(k+1) /(k+1))= ⇒ln(1+s)=Σ_(k=1) ^∞ (((−1)^(k−1) s^k )/k) ⇒Σ_(k=1) ^n (((−1)^(k−1) )/k)=ln(2)−Σ_(k=n+1) ^∞ (((−1)^(k−1) )/k) ⇒A_n =(−1)^n Σ_(k=n+1) ^∞ (((−1)^(k−1) )/k) ⇒lim_(n→∞) A_n =0](Q172318.png) | ||
| ||
Answered by Mathspace last updated on 25/Jun/22 | ||
![A_n =∫_R^+ (x^n /(1+x))χ_([0,1]) (x)dx =∫_R^+ f_n (x)dx f_m converge simplement vers0 car x ∈[0,1] and f_n est dominee par g(x)=(1/(1+x)) ⇒lim A_n =∫_R^+ lim f_n =0](Q172330.png) | ||
| ||
Answered by puissant last updated on 25/Jun/22 | ||
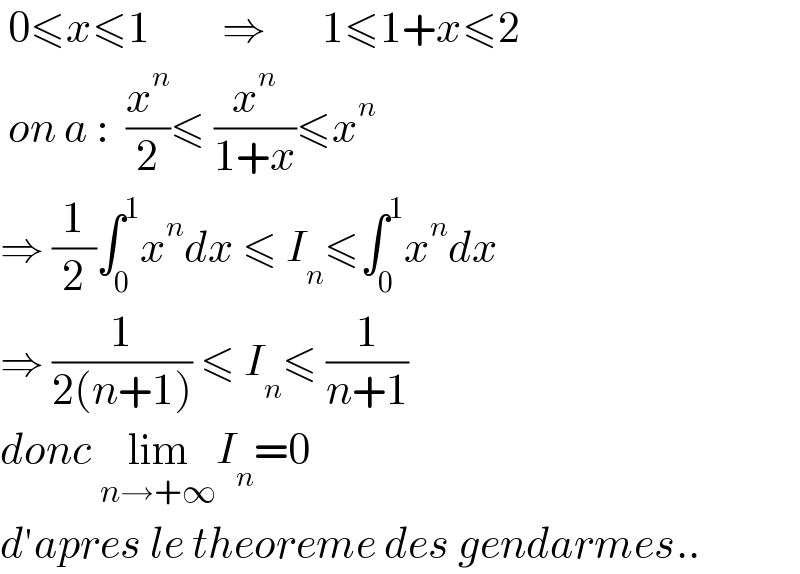 | ||
| ||