Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 172453 by mr W last updated on 27/Jun/22

Commented by infinityaction last updated on 27/Jun/22

22 ????

$$\mathrm{22}\:???? \\ $$

Commented by mr W last updated on 27/Jun/22

yes. please show your working.

$${yes}.\:{please}\:{show}\:{your}\:{working}. \\ $$

Commented by infinityaction last updated on 27/Jun/22

Commented by infinityaction last updated on 27/Jun/22

△OQR∼△RTQ (6/8) = (((QR)/(RT)))^2 ⇒ ((QR)/(RT)) = ((√3)/2) let QR = (√3)k and RT = 2k then QT = (√(4k^2 −3k^2 )) = k in △PSQ tan30° = (((√3)k)/(PQ)) PQ = 3k PT = PQ−TQ = 3k−k = 2k now △PQS ∼△TQR ((A+2)/8) = (((3k)/( (√3)k)))^2 A+2 = 24 A = 22

$$\:\:\:\bigtriangleup{OQR}\sim\bigtriangleup{RTQ} \\ $$$$\:\:\:\:\frac{\mathrm{6}}{\mathrm{8}}\:\:=\:\:\left(\frac{{QR}}{{RT}}\right)^{\mathrm{2}} \:\:\Rightarrow\:\:\frac{{QR}}{{RT}}\:\:\:=\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:{let}\:\:\:\:\:{QR}\:\:=\:\:\sqrt{\mathrm{3}}{k}\:\:{and}\:\:{RT}\:\:=\:\:\mathrm{2}{k} \\ $$$$\:\:\:\:{then}\:\:{QT}\:\:=\:\:\:\sqrt{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} \:}\:\:=\:\:{k} \\ $$$$\:\:\:{in}\:\bigtriangleup{PSQ} \\ $$$$\:\:\:\:\mathrm{tan30}°\:\:=\:\:\frac{\sqrt{\mathrm{3}}{k}}{{PQ}} \\ $$$$\:\:\:\:{PQ}\:\:=\:\:\mathrm{3}{k} \\ $$$$\:\:\:\:\:{PT}\:\:=\:\:{PQ}−{TQ}\:=\:\mathrm{3}{k}−{k}\:=\:\mathrm{2}{k} \\ $$$$\:\:\:\:{now}\:\:\:\bigtriangleup{PQS}\:\sim\bigtriangleup{TQR} \\ $$$$\:\:\:\frac{{A}+\mathrm{2}}{\mathrm{8}}\:\:\:=\:\:\left(\frac{\mathrm{3}{k}}{\:\sqrt{\mathrm{3}}{k}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:{A}+\mathrm{2}\:\:=\:\:\mathrm{24} \\ $$$$\:\:\:\:{A}\:\:=\:\mathrm{22} \\ $$

Commented by mr W last updated on 27/Jun/22

thanks sir!

$${thanks}\:{sir}! \\ $$

Commented by infinityaction last updated on 27/Jun/22

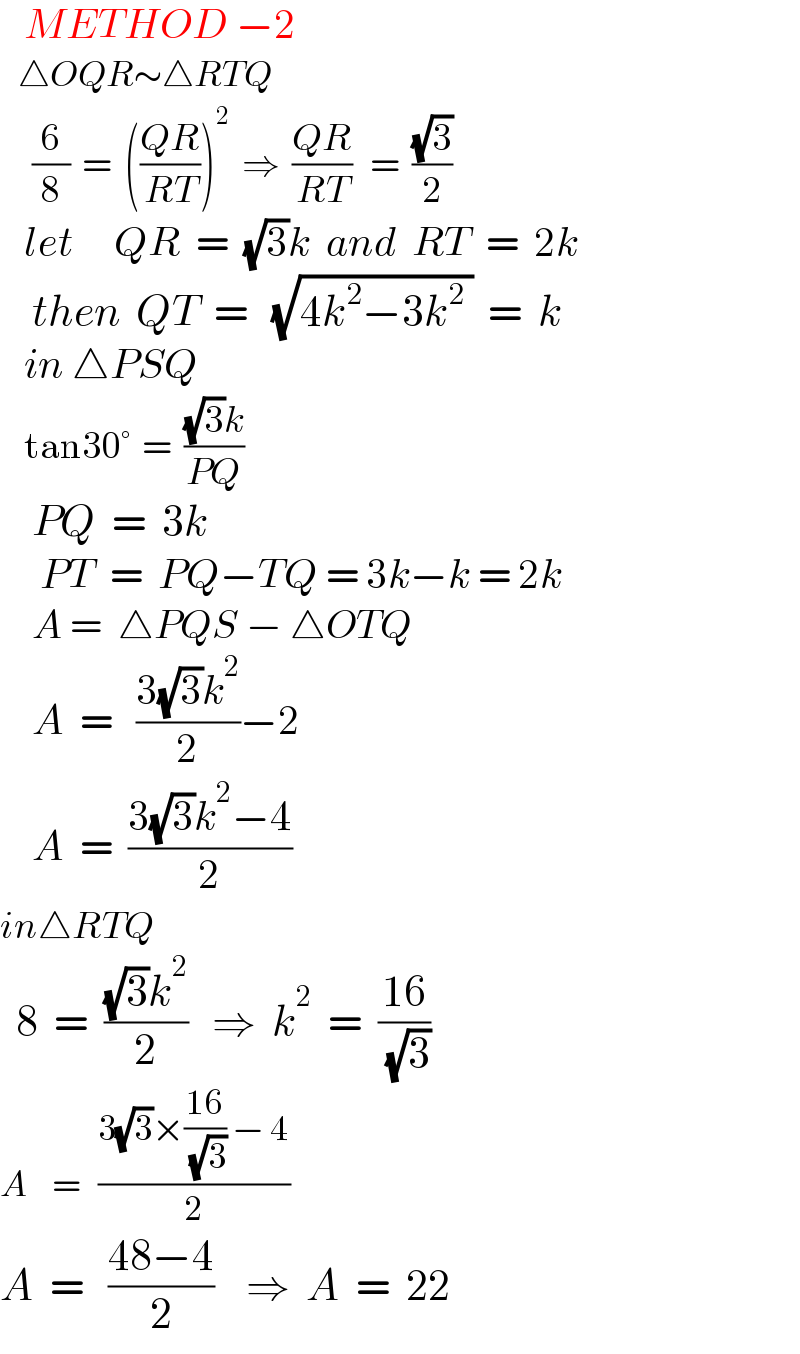
METHOD −2 △OQR∼△RTQ (6/8) = (((QR)/(RT)))^2 ⇒ ((QR)/(RT)) = ((√3)/2) let QR = (√3)k and RT = 2k then QT = (√(4k^2 −3k^2 )) = k in △PSQ tan30° = (((√3)k)/(PQ)) PQ = 3k PT = PQ−TQ = 3k−k = 2k A = △PQS − △OTQ A = ((3(√3)k^2 )/2)−2 A = ((3(√3)k^2 −4)/2) in△RTQ 8 = (((√3)k^2 )/2) ⇒ k^2 = ((16)/( (√3))) A = ((3(√3)×((16)/( (√3))) − 4)/2) A = ((48−4)/2) ⇒ A = 22

$$\:\:\:{METHOD}\:−\mathrm{2} \\ $$$$\:\:\:\bigtriangleup{OQR}\sim\bigtriangleup{RTQ} \\ $$$$\:\:\:\:\frac{\mathrm{6}}{\mathrm{8}}\:\:=\:\:\left(\frac{{QR}}{{RT}}\right)^{\mathrm{2}} \:\:\Rightarrow\:\:\frac{{QR}}{{RT}}\:\:\:=\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:{let}\:\:\:\:\:{QR}\:\:=\:\:\sqrt{\mathrm{3}}{k}\:\:{and}\:\:{RT}\:\:=\:\:\mathrm{2}{k} \\ $$$$\:\:\:\:{then}\:\:{QT}\:\:=\:\:\:\sqrt{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{3}{k}^{\mathrm{2}} \:}\:\:=\:\:{k} \\ $$$$\:\:\:{in}\:\bigtriangleup{PSQ} \\ $$$$\:\:\:\:\mathrm{tan30}°\:\:=\:\:\frac{\sqrt{\mathrm{3}}{k}}{{PQ}} \\ $$$$\:\:\:\:{PQ}\:\:=\:\:\mathrm{3}{k} \\ $$$$\:\:\:\:\:{PT}\:\:=\:\:{PQ}−{TQ}\:=\:\mathrm{3}{k}−{k}\:=\:\mathrm{2}{k} \\ $$$$\:\:\:\:{A}\:=\:\:\bigtriangleup{PQS}\:−\:\bigtriangleup{OTQ} \\ $$$$\:\:\:\:{A}\:\:=\:\:\:\frac{\mathrm{3}\sqrt{\mathrm{3}}{k}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2} \\ $$$$\:\:\:\:{A}\:\:=\:\:\frac{\mathrm{3}\sqrt{\mathrm{3}}{k}^{\mathrm{2}} −\mathrm{4}}{\mathrm{2}} \\ $$$${in}\bigtriangleup{RTQ} \\ $$$$\:\:\mathrm{8}\:\:=\:\:\frac{\sqrt{\mathrm{3}}{k}^{\mathrm{2}} }{\mathrm{2}}\:\:\:\Rightarrow\:\:{k}^{\mathrm{2}} \:\:=\:\:\frac{\mathrm{16}}{\:\sqrt{\mathrm{3}}} \\ $$$${A}\:\:\:\:=\:\:\:\frac{\mathrm{3}\sqrt{\mathrm{3}}×\frac{\mathrm{16}}{\:\sqrt{\mathrm{3}}}\:−\:\mathrm{4}}{\mathrm{2}} \\ $$$${A}\:\:=\:\:\:\frac{\mathrm{48}−\mathrm{4}}{\mathrm{2}}\:\:\:\:\Rightarrow\:\:{A}\:\:=\:\:\mathrm{22} \\ $$

Answered by mr W last updated on 27/Jun/22

Commented by mr W last updated on 27/Jun/22

ΔEFB∼ΔBFC∼ΔCFD (((BF)/(EF)))^2 =(([ΔBFC])/([ΔEFB]))=(6/2)=3 ⇒((BF)/(EF))=(√3) ((CF)/(BF))=((BF)/(EF))=(√3) ((CF)/(EF))=((CF)/(BF))×((BF)/(EF))=(√3)×(√3)=3 (([ΔCFD])/([ΔEFB]))=(((CF)/(EF)))^2 =3^2 =9 S=[ΔCFD]=9×[ΔEFB]=9×2=18 T+2=S+6=18+6=24 ?=T=24−2=22 ✓

$$\Delta{EFB}\sim\Delta{BFC}\sim\Delta{CFD} \\ $$$$\left(\frac{{BF}}{{EF}}\right)^{\mathrm{2}} =\frac{\left[\Delta{BFC}\right]}{\left[\Delta{EFB}\right]}=\frac{\mathrm{6}}{\mathrm{2}}=\mathrm{3}\:\Rightarrow\frac{{BF}}{{EF}}=\sqrt{\mathrm{3}} \\ $$$$\frac{{CF}}{{BF}}=\frac{{BF}}{{EF}}=\sqrt{\mathrm{3}} \\ $$$$\frac{{CF}}{{EF}}=\frac{{CF}}{{BF}}×\frac{{BF}}{{EF}}=\sqrt{\mathrm{3}}×\sqrt{\mathrm{3}}=\mathrm{3} \\ $$$$\frac{\left[\Delta{CFD}\right]}{\left[\Delta{EFB}\right]}=\left(\frac{{CF}}{{EF}}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$$${S}=\left[\Delta{CFD}\right]=\mathrm{9}×\left[\Delta{EFB}\right]=\mathrm{9}×\mathrm{2}=\mathrm{18} \\ $$$${T}+\mathrm{2}={S}+\mathrm{6}=\mathrm{18}+\mathrm{6}=\mathrm{24} \\ $$$$?={T}=\mathrm{24}−\mathrm{2}=\mathrm{22}\:\checkmark \\ $$

Commented by infinityaction last updated on 27/Jun/22

nice solution

$${nice}\:{solution} \\ $$

Commented by mr W last updated on 27/Jun/22

in principle we had similar way for solution.

$${in}\:{principle}\:{we}\:{had}\:{similar}\:{way}\:{for} \\ $$$${solution}. \\ $$

Commented by infinityaction last updated on 27/Jun/22

yes sir

$${yes}\:{sir} \\ $$

Commented by Tawa11 last updated on 28/Jun/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com