Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 172681 by mnjuly1970 last updated on 30/Jun/22

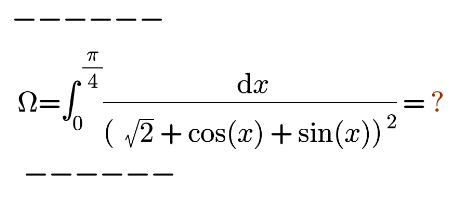
Answered by Jamshidbek last updated on 30/Jun/22

$$\mathrm{Hint}:\mathrm{Lemma}:{\int }_{\mathrm{a}}^{\mathrm{b}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}={\int }_{\mathrm{a}}^{\mathrm{b}}\mathrm{f}(\mathrm{a}+\mathrm{b}-\mathrm{x})\mathrm{dx}$$$$\mathrm{after}\mathrm{tg}\frac{\mathrm{x}}{2}=\mathrm{t}.$$

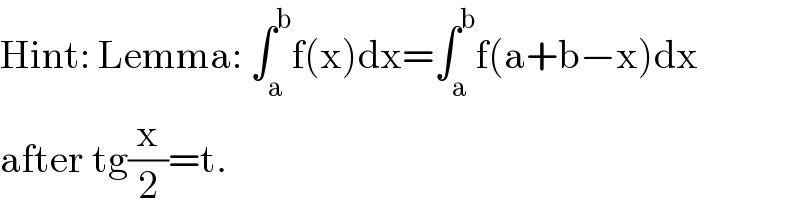
Answered by Mathspace last updated on 30/Jun/22

$$$$$$f\left(a\right)={\int }_0^{\frac{\pi }{4}}\frac{dx}{a+cosx+sinx}$$$$\Rightarrow f^{{}^{\prime }}\left(a\right)=-{\int }_0^{\frac{\pi }{4}}\frac{dx}{{(a+cosx+sinx)}^2}$$$$\Rightarrow {\int }_0^{\frac{\pi }{4}}\frac{dx}{{(a+cosx+sinx)}^2}=-f^{{}^{\prime }}\left(a\right)$$$$\Rightarrow I=-f^{{}^{\prime }}\left(\sqrt{2}\right)$$$$wetakea>1$$$$f\left(a\right){=}_{tan\left(\frac{x}{2}\right)=t}{\int }_0^{\sqrt{2}-1}\frac{2dt}{(1+t^2)(a+\frac{1-t^2}{1+t^2}+\frac{2t}{1+t^2})}$$

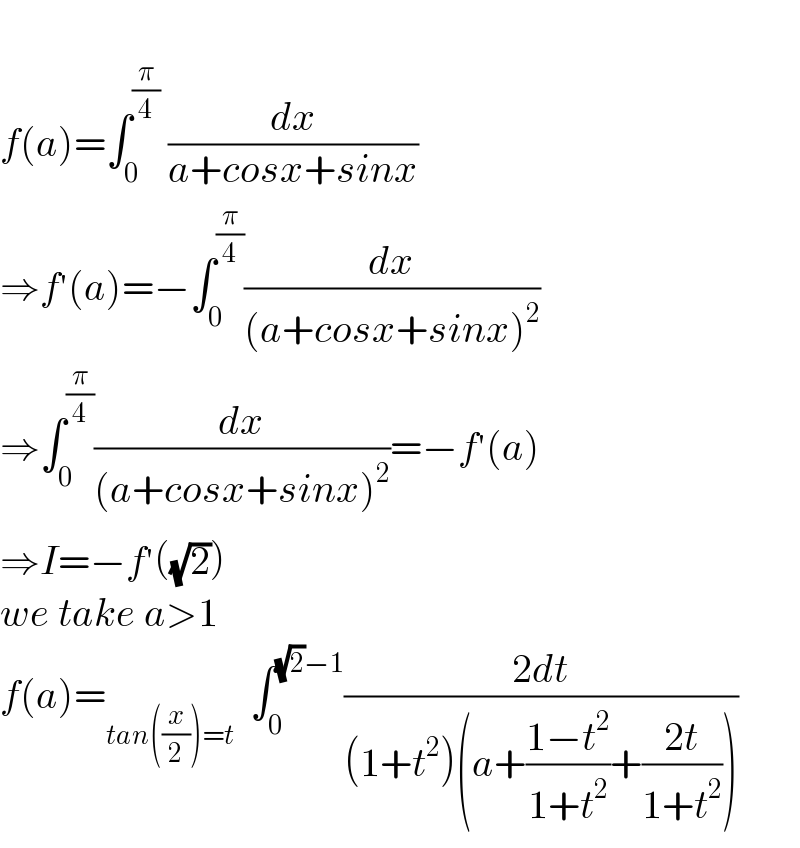
Commented by Mathspace last updated on 30/Jun/22

$$f\left(a\right)=2{\int }_0^{\sqrt{2}-1}\frac{dt}{a+{at}^2+1-t^2+2t}$$$$=2{\int }_0^{\sqrt{2}-1}\frac{dt}{(a-1)t^2+2t+a+1}$$$${\mathrm{\Delta }}^{{}^{\prime }}=1-(a^2-1)=2-a^2$$$$t_1=\frac{-1+\sqrt{2-a^2}}{a-1}$$$$t_2=\frac{-1-\sqrt{2-a^2}}{a-1}\Rightarrow$$$$f\left(a\right)=2{\int }_0^{\sqrt{2}-1}\frac{dt}{(a-1)(t-t_1)(t-t_2)}$$$$=\frac{2}{a-1}\times \frac{2\sqrt{2-a^2}}{a-1}{\int }_0^{\sqrt{2}-1}(\frac{1}{t-t_1}-\frac{1}{t-t_2})dt$$$$=\frac{4\sqrt{2-a^2}}{{(a-1)}^2}{[ln\mid \frac{t-t_1}{t-t_2}\mid ]}_0^{\sqrt{2}-1}$$$$=\frac{4\sqrt{2-a^2}}{{(a-1)}^2}\{ln\mid \frac{\sqrt{2}-1-t_1}{\sqrt{2}-1-t_2}\mid +ln\mid \frac{t_2}{t_1}\mid \}$$$$resttocalculate{f}^{{}^{\prime }}\left(a\right)...becontinued...$$

Answered by Mathspace last updated on 30/Jun/22

$$\mathrm{\Phi }={\int }_0^{\frac{\pi }{4}}\frac{dx}{{(\sqrt{2}+\sqrt{2}cos(x-\frac{\pi }{4}))}^2}$$$$=\frac{1}{2}{\int }_0^{\frac{\pi }{4}}\frac{dx}{{(1+cos(x-\frac{\pi }{4}))}^2}$$$${=}_{x-\frac{\pi }{4}=-t}\frac{1}{2}{\int }_{\frac{\pi }{4}}^o\frac{-dt}{{(1+cost)}^2}$$$$=\frac{1}{2}{\int }_0^{\frac{\pi }{4}}\frac{dt}{{(1+cost)}^2}(tan\left(\frac{t}{2}\right)=y)$$$$=\frac{1}{2}{\int }_0^{\sqrt{2}-1}\frac{2dy}{(y^2+1){(1+\frac{1-y^2}{1+y^2})}^2}$$$$={\int }_0^{\sqrt{2}-1}\frac{dy}{(y^2+1){\left(\frac{2}{1+y^2}\right)}^2}$$$$={\int }_0^{\sqrt{2}-1}\frac{1+y^2}{4}dy$$$$=\frac{1}{4}(\sqrt{2}-1)+\frac{1}{12}{\left[y^3\right]}_0^{\sqrt{2}-1}$$$$=\frac{\sqrt{2}-1}{4}+\frac{{(\sqrt{2}-1)}^3}{12}$$

Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\mathrm{sir}$$

Answered by mr W last updated on 30/Jun/22

$$\cos x+\sin x=\sqrt{2}\cos (x-\frac{\pi }{4})$$$$\mathrm{\Omega }={\int }_0^{\frac{\pi }{4}}\frac{d(x-\frac{\pi }{4})}{2{(1+\cos (x-\frac{\pi }{4}))}^2}$$$$\mathrm{\Omega }={\int }_{-\frac{\pi }{4}}^0\frac{dt}{2{(1+\cos t)}^2}$$$$\mathrm{\Omega }=\frac{1}{4}{\int }_{-\frac{\pi }{4}}^0\frac{d\left(\frac{t}{2}\right)}{{\cos }^4\left(\frac{t}{2}\right)}$$$$\mathrm{\Omega }=\frac{1}{4}{\int }_{-\frac{\pi }{8}}^0\frac{du}{{\cos }^{4}u}$$$$\mathrm{\Omega }=\frac{1}{4}{[\tan u+\frac{{\tan }^{3}u}{3}]}_{-\frac{\pi }{8}}^0$$$$\mathrm{\Omega }=\frac{1}{4}\tan \frac{\pi }{8}(1+\frac{1}{3}\times {\tan }^2\frac{\pi }{8})$$$$\mathrm{\Omega }=\frac{\sqrt{2}-1}{4}(1+\frac{{(\sqrt{2}-1)}^2}{3})=\frac{4\sqrt{2}-5}{6}✓$$$$$$$$\tan \frac{\pi }{4}=\frac{2\tan \frac{\pi }{8}}{1-{\tan }^2\frac{\pi }{8}}=1$$$$\Rightarrow \tan \frac{\pi }{8}=\sqrt{2}-1$$

Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com