
Question Number 172775 by Shrinava last updated on 01/Jul/22

Answered by mahdipoor last updated on 02/Jul/22

$${get}\:{side}\:{of}\:{square}\:=\:{a} \\ $$$${and}\:{cotB}+{cotC}={b} \\ $$$$, \\ $$$${BQ}={MQ}.{cotB}={a}.{cotB} \\ $$$${PC}={NP}.{cotC}={a}.{cotC} \\ $$$${BC}={BQ}+{QP}+{PC}={a}\left(\mathrm{1}+{cotB}+{cotC}\right) \\ $$$$\begin{cases}{\frac{{AM}}{{AB}}=\frac{{MN}}{{BC}}=\frac{\mathrm{1}}{\mathrm{1}+{cotB}+{cotC}}}\\{{AM}={AB}−{MB}={AB}−{MQ}.{cscB}={AB}−{a}.{cscB}}\end{cases} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{1}+{cotB}+{cotC}}{{cotB}+{cotC}}×{a}.{cscB} \\ $$$${S}\left(\Box\right)={a}^{\mathrm{2}} \\ $$$${S}\left(\Delta\right)=\frac{{AB}.{BC}.{sinB}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\left(\mathrm{1}+{cotB}+{cotC}\right)^{\mathrm{2}} }{{cotB}+{cotC}}\right) \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{{b}}+\mathrm{2}+{b}\right)\:\Rightarrow\:\frac{\mathrm{1}}{{b}}+{b}\geqslant\mathrm{2}\:\Rightarrow \\ $$$${S}\left(\Delta\right)\geqslant\mathrm{2}{a}^{\mathrm{2}} \\ $$$$\Rightarrow{S}\left(\Box\right)\leqslant\mathrm{0}.\mathrm{5}×{S}\left(\Delta\right) \\ $$
Answered by aleks041103 last updated on 01/Jul/22
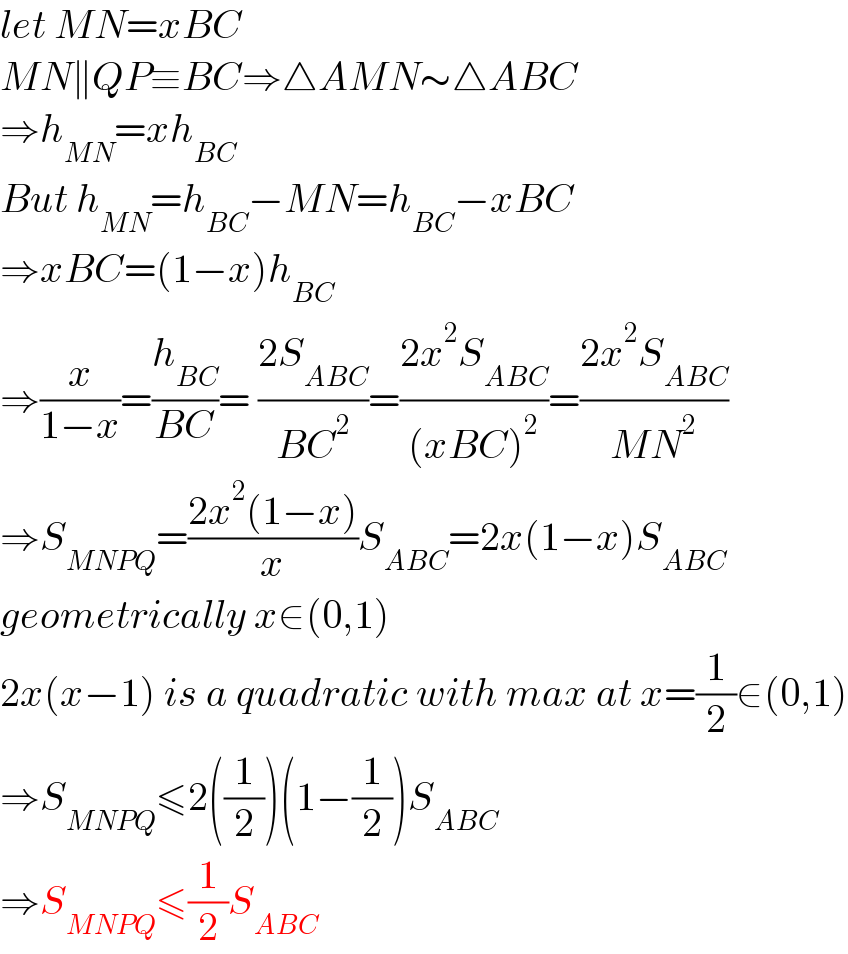
$${let}\:{MN}={xBC} \\ $$$${MN}\parallel{QP}\equiv{BC}\Rightarrow\bigtriangleup{AMN}\sim\bigtriangleup{ABC} \\ $$$$\Rightarrow{h}_{{MN}} ={xh}_{{BC}} \\ $$$${But}\:{h}_{{MN}} ={h}_{{BC}} −{MN}={h}_{{BC}} −{xBC} \\ $$$$\Rightarrow{xBC}=\left(\mathrm{1}−{x}\right){h}_{{BC}} \\ $$$$\Rightarrow\frac{{x}}{\mathrm{1}−{x}}=\frac{{h}_{{BC}} }{{BC}}=\:\frac{\mathrm{2}{S}_{{ABC}} }{{BC}^{\mathrm{2}} }=\frac{\mathrm{2}{x}^{\mathrm{2}} {S}_{{ABC}} }{\left({xBC}\right)^{\mathrm{2}} }=\frac{\mathrm{2}{x}^{\mathrm{2}} {S}_{{ABC}} }{{MN}^{\mathrm{2}} } \\ $$$$\Rightarrow{S}_{{MNPQ}} =\frac{\mathrm{2}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{{x}}{S}_{{ABC}} =\mathrm{2}{x}\left(\mathrm{1}−{x}\right){S}_{{ABC}} \\ $$$${geometrically}\:{x}\in\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\mathrm{2}{x}\left({x}−\mathrm{1}\right)\:{is}\:{a}\:{quadratic}\:{with}\:{max}\:{at}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\in\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\Rightarrow{S}_{{MNPQ}} \leqslant\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right){S}_{{ABC}} \\ $$$$\Rightarrow{S}_{{MNPQ}} \leqslant\frac{\mathrm{1}}{\mathrm{2}}{S}_{{ABC}} \\ $$
Commented by aleks041103 last updated on 01/Jul/22

$${eqiality}\:{at}\:{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{h}_{{BC}} ={BC}×\frac{{x}}{\mathrm{1}−{x}}={BC} \\ $$$$\Rightarrow{Equality}\:{at}\:{h}_{{BC}} ={BC} \\ $$
Commented by Shrinava last updated on 02/Jul/22

$$\mathrm{Cool}\:\mathrm{professor}\:\mathrm{than}\:\mathrm{you} \\ $$
