Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 172838 by DAVONG last updated on 02/Jul/22

1.lim_(x→1) ((x−1−lnx)/(x^2 −2x+1)) = ?

$$\mathrm{1}.\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{x}−\mathrm{1}−\mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}\:=\:? \\ $$

Commented by cortano1 last updated on 02/Jul/22

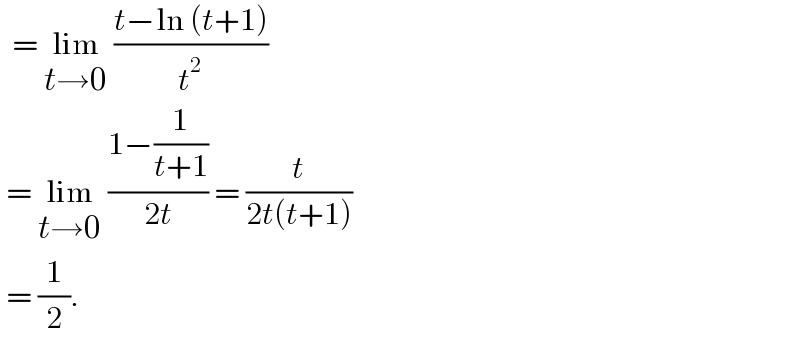
= lim_(t→0) ((t−ln (t+1))/t^2 ) = lim_(t→0) ((1−(1/(t+1)))/(2t)) = (t/(2t(t+1))) = (1/2).

$$\:\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{t}−\mathrm{ln}\:\left({t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} }\: \\ $$$$\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{\mathrm{1}}{{t}+\mathrm{1}}}{\mathrm{2}{t}}\:=\:\frac{{t}}{\mathrm{2}{t}\left({t}+\mathrm{1}\right)} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}.\: \\ $$

Answered by CElcedricjunior last updated on 02/Jul/22

lim_(x→1) ((x−1−lnx)/(x^2 −2x+1))=lim_(x→1) ((1−(1/x))/(2x−2))=lim_(x→1) ((1/x^2 )/2) lim_(x→1) ((x−1−lnx)/(x^2 −2x+1))=(1/2) ...........Le celebre cedric junior..........

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{x}}−\mathrm{1}−\boldsymbol{\mathrm{lnx}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{1}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}−\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}}{\mathrm{2}\boldsymbol{\mathrm{x}}−\mathrm{2}}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{x}}−\mathrm{1}−\boldsymbol{\mathrm{lnx}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{\mathrm{x}}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\: \\ $$$$\: \\ $$$$\:...........\mathscr{L}\boldsymbol{\mathrm{e}}\:{celebre}\:{cedric}\:{junior}.......... \\ $$

Commented by DAVONG last updated on 03/Jul/22

Tanks teacher!

$$\mathrm{Tanks}\:\mathrm{teacher}! \\ $$

Answered by Mathspace last updated on 02/Jul/22

=lim_(x→1) ((1−(1/x))/(2x−2)) =lim_(x→1) ((x−1)/(2x(x−1))) =lim_(x→1) (1/(2x))=(1/2)(by hospital) another way let f(x)=((x−1−lnx)/(x^2 −2x+1))=((x−1−lnx)/((x−1)^2 )) we do the changement x−1=t (so t→0) ⇒ f(x)=f(t+1)=((t−ln(t+1))/t^2 ) ln^′ (1+t)=(1/(1+t))=1−t+(t^2 /2)+o(t^3 ) ⇒ ln(1+t)=t−(t^2 /2)+o(t^3 )⇒ f(1+t)∼((t−t+(t^2 /2))/t^2 )=(1/2) ⇒lim_(t→) f(1+t)=(1/2) =lim_(x→0) f(x)

$$={lim}_{{x}\rightarrow\mathrm{1}} \frac{\mathrm{1}−\frac{\mathrm{1}}{{x}}}{\mathrm{2}{x}−\mathrm{2}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{1}} \frac{{x}−\mathrm{1}}{\mathrm{2}{x}\left({x}−\mathrm{1}\right)} \\ $$$$={lim}_{{x}\rightarrow\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{2}}\left({by}\:{hospital}\right) \\ $$$${another}\:{way} \\ $$$${let}\:{f}\left({x}\right)=\frac{{x}−\mathrm{1}−{lnx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}}=\frac{{x}−\mathrm{1}−{lnx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${we}\:{do}\:{the}\:{changement} \\ $$$${x}−\mathrm{1}={t}\:\:\:\left({so}\:{t}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$${f}\left({x}\right)={f}\left({t}+\mathrm{1}\right)=\frac{{t}−{ln}\left({t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} } \\ $$$${ln}^{'} \left(\mathrm{1}+{t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}}=\mathrm{1}−{t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({t}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{t}\right)={t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+{o}\left({t}^{\mathrm{3}} \right)\Rightarrow \\ $$$${f}\left(\mathrm{1}+{t}\right)\sim\frac{{t}−{t}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}}{{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{lim}_{{t}\rightarrow} \:{f}\left(\mathrm{1}+{t}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$={lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right) \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com