
Question and Answers Forum
Question Number 173033 by cortano1 last updated on 05/Jul/22

Answered by greougoury555 last updated on 05/Jul/22
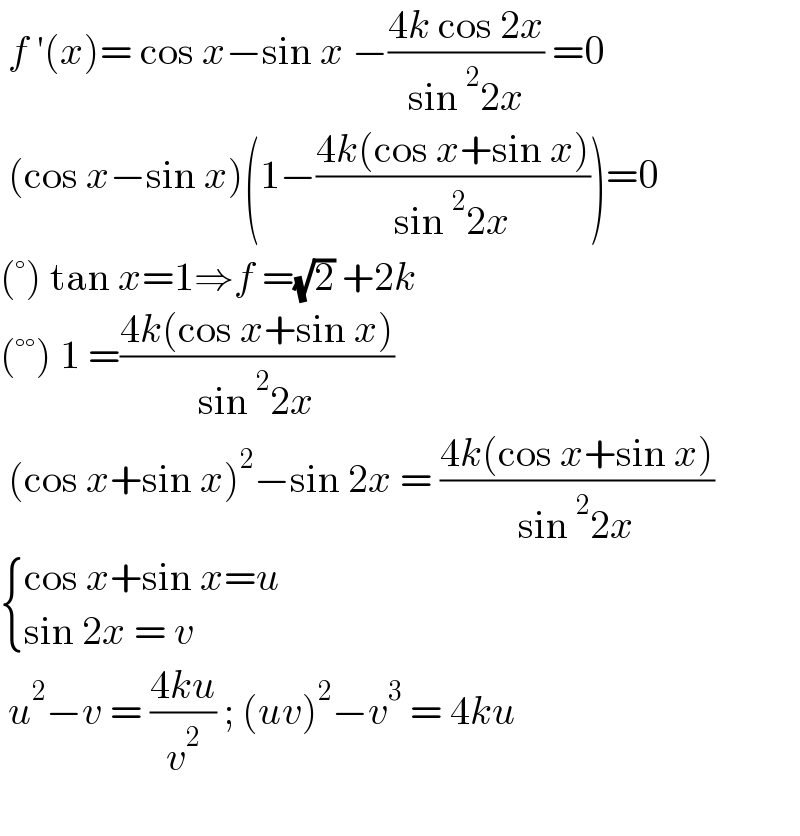
Answered by a.lgnaoui last updated on 05/Jul/22
![f(x)=sin x+cos x+((2k)/(sin 2x)) limf(x)_(x→0) =1+(1/x)lim_(x→0) ((2x)/(sin 2x))k=1+(k/x) if k>0 f→+∞; if k<0 f→−∞ lim_(x→(π/2)) f(x)=1+lim_(x→(π/2)) ((2k)/(sin 2x))=+∞ if k>0 or −∞ if k<0 donc f decroissant et criissant si k>0 et contraire pour k>0 f′(x)=cos x−sin x−k((cos^2 x−sin^2 x)/(sin^2 xcos^2 x))=(cos x−sin x)[1−k((1/(cos x))+(1/(sin x)))] remarque x=(π/4) ⇒f′(x)=0 donc (π/4) is minimum of f(x).](Q173040.png)
| ||
Question and Answers Forum | ||
Question Number 173033 by cortano1 last updated on 05/Jul/22 | ||
 | ||
Answered by greougoury555 last updated on 05/Jul/22 | ||
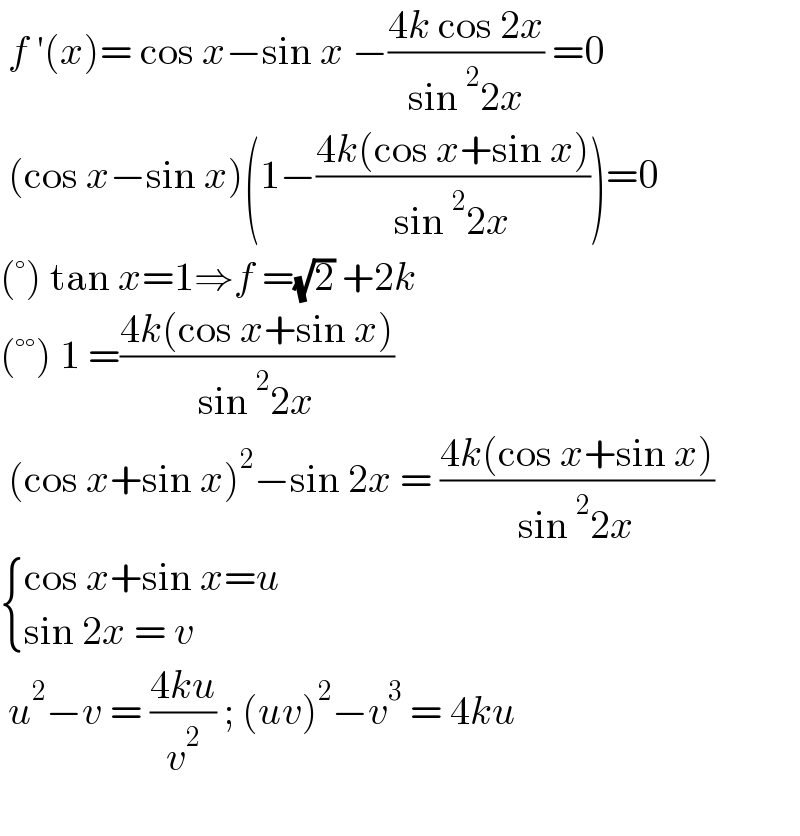 | ||
| ||
Answered by a.lgnaoui last updated on 05/Jul/22 | ||
![f(x)=sin x+cos x+((2k)/(sin 2x)) limf(x)_(x→0) =1+(1/x)lim_(x→0) ((2x)/(sin 2x))k=1+(k/x) if k>0 f→+∞; if k<0 f→−∞ lim_(x→(π/2)) f(x)=1+lim_(x→(π/2)) ((2k)/(sin 2x))=+∞ if k>0 or −∞ if k<0 donc f decroissant et criissant si k>0 et contraire pour k>0 f′(x)=cos x−sin x−k((cos^2 x−sin^2 x)/(sin^2 xcos^2 x))=(cos x−sin x)[1−k((1/(cos x))+(1/(sin x)))] remarque x=(π/4) ⇒f′(x)=0 donc (π/4) is minimum of f(x).](Q173040.png) | ||
| ||