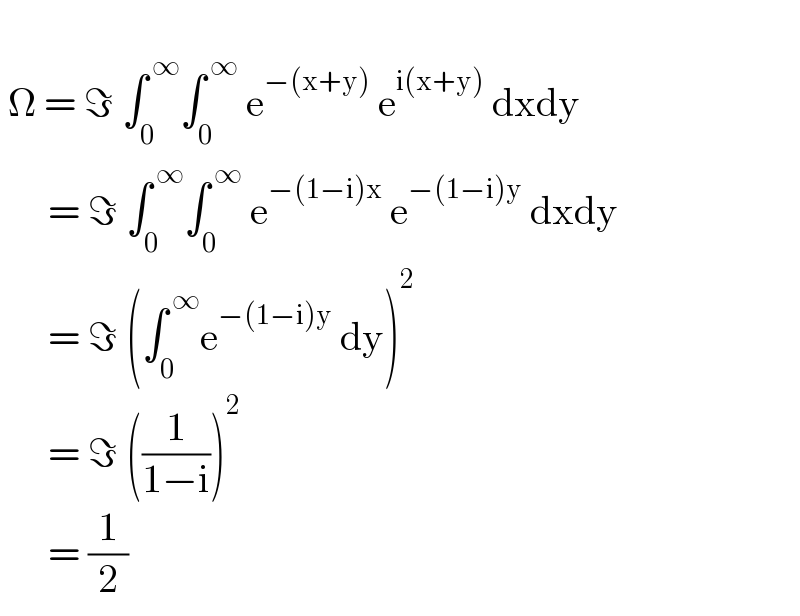Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 173068 by mnjuly1970 last updated on 06/Jul/22

	Answered by Mathspace last updated on 06/Jul/22
	$Φ=∫_0 ^∞ (∫_0 ^∞ e^(−x) sin(x+y)dx)e^(−y) dy but ∫_0 ^∞ e^(−x) sin(x+y)dx =Im(∫_0 ^∞ e^(−x+i(x+y)) dx)and ∫_0 ^∞ e^(−x+i(x+y)) dx =e^(iy) ∫_0 ^∞ e^((−1+i)x) dx =e^(iy) [(1/(−1+i))e^((−1+i)x) ]_0 ^∞ =e^(iy) (−(1/(−1+i)))=(e^(ih) /(1−i)) =(((1+i)e^(iy) )/2)=(((1+i)(cosy+isiny))/2) =(1/2){cosy+isiny+icosy−siny} ⇒Im(...)=(1/2)(cosy+siny)⇒ Φ=∫_0 ^∞ (1/2)(cosy+siny)e^(−y) dy 2Φ=Re(∫_0 ^∞ e^(−y+iy) dy)+Im(∫_0 ^∞ e^(−y+iy) dy) or ∫_0 ^∞ e^((−1+i)y) dy =[(1/(−1+i))e^((−1+i)y) ]_0 ^∞ =(1/(1−i)) =((1+i)/2) ⇒Re(....)=(1/2) and Im(...)=(1/2) ⇒ 2Φ=1 ⇒Φ=(1/2)$
	$Φ = \int_{0}^{\infty} (\int_{0}^{\infty} e^{- x} s i n (x + y) d x) e^{- y} d y$ $b u t \int_{0}^{\infty} e^{- x} s i n (x + y) d x$ $= I m (\int_{0}^{\infty} e^{- x + i (x + y)} d x) a n d$ $\int_{0}^{\infty} e^{- x + i (x + y)} d x$ $= e^{i y} \int_{0}^{\infty} e^{(- 1 + i) x} d x$ $= e^{i y} {[\frac{1}{- 1 + i} e^{(- 1 + i) x}]}_{0}^{\infty}$ $= e^{i y} (- \frac{1}{- 1 + i}) = \frac{e^{i h}}{1 - i}$ $= \frac{(1 + i) e^{i y}}{2} = \frac{(1 + i) (c o s y + i s i n y)}{2}$ $= \frac{1}{2} {c o s y + i s i n y + i c o s y - s i n y}$ $\Rightarrow I m (. . .) = \frac{1}{2} (c o s y + s i n y) \Rightarrow$ $Φ = \int_{0}^{\infty} \frac{1}{2} (c o s y + s i n y) e^{- y} d y$ $2 Φ = R e (\int_{0}^{\infty} e^{- y + i y} d y) + I m (\int_{0}^{\infty} e^{- y + i y} d y)$ $o r \int_{0}^{\infty} e^{(- 1 + i) y} d y$ $= {[\frac{1}{- 1 + i} e^{(- 1 + i) y}]}_{0}^{\infty} = \frac{1}{1 - i}$ $= \frac{1 + i}{2} \Rightarrow R e (. . . .) = \frac{1}{2}$ $a n d I m (. . .) = \frac{1}{2} \Rightarrow$ $2 Φ = 1 \Rightarrow Φ = \frac{1}{2}$
	Commented by mnjuly1970 last updated on 06/Jul/22

	$bravo sir . .$
	Commented by Mathspace last updated on 06/Jul/22

	$y o u a r e w e l c o m e$
	Answered by Eulerian last updated on 07/Jul/22

	$Ω = ℑ \int_{0}^{\infty} \int_{0}^{\infty} e^{- (x + y)} e^{i (x + y)} dxdy$ $= ℑ \int_{0}^{\infty} \int_{0}^{\infty} e^{- (1 - i) x} e^{- (1 - i) y} dxdy$ $= ℑ {(\int_{0}^{\infty} e^{- (1 - i) y} dy)}^{2}$ $= ℑ {(\frac{1}{1 - i})}^{2}$ $= \frac{1}{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum