
Question and Answers Forum
Question Number 173150 by Frix last updated on 07/Jul/22
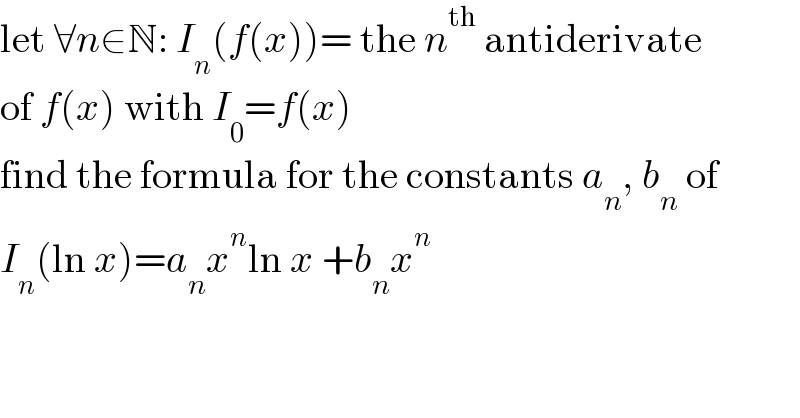
Answered by aleks041103 last updated on 07/Jul/22
![I_(n+1) (ln x)=∫I_n (ln x)dx= =∫(a_n x^n ln x + b_n x^n )dx= =a_n ∫x^n ln x dx + b_n ∫x^n dx ∫x^n ln x dx=∫ln x d((x^(n+1) /(n+1)))= =(x^(n+1) /(n+1))ln x−(1/(n+1))∫x^(n+1) (dx/x)= =(1/(n+1))x^(n+1) ln x −(1/((n+1)^2 ))x^(n+1) ⇒I_(n+1) (ln x)=a_n [(1/(n+1))x^(n+1) ln x −(1/((n+1)^2 ))x^(n+1) ]+(b_n /(n+1))x^(n+1) = =((a_n /(n+1)))x^(n+1) ln x + ((b_n /(n+1))−(a_n /((n+1)^2 )))x^(n+1) = =a_(n+1) x^(n+1) ln x + b_(n+1) x^(n+1) ⇒ { ((a_(n+1) =(a_n /(n+1)))),((b_(n+1) =(b_n /(n+1))−(a_n /((n+1)^2 )))) :} (1/a_(n+1) )=(n+1)(1/a_n )⇒(1/a_n )=const.n!⇒a_n =((const)/(n!)) I_0 (ln x)=ln x⇒a_0 =1⇒a_n =(1/(n!)) ⇒b_(n+1) =(b_n /(n+1))−(1/((n+1)!(n+1))) (n+1)b_(n+1) −b_n =−(1/((n+1)!)) b_n =(c_n /(n!)) ⇒(n+1)(c_(n+1) /((n+1)!))−(c_n /(n!))=−(1/((n+1)!))=−(1/((n+1) n!)) ⇒c_(n+1) −c_n =−(1/(n+1)) ⇒c_n =const.−Σ_(i≥1) ^n (1/i) c_0 =const.=0⇒c_n =−Σ_(i≥1) ^n (1/i)=−H_n ⇒b_n =−(H_n /(n!)) ⇒ { ((a_n =(1/(n!)))),((b_n =−(H_n /(n!)) , H_(n≥1) =Σ_(k=1) ^n (1/k), H_0 =0)) :}](Q173158.png)
Commented by Frix last updated on 08/Jul/22

Commented by Tawa11 last updated on 11/Jul/22

| ||
Question and Answers Forum | ||
Question Number 173150 by Frix last updated on 07/Jul/22 | ||
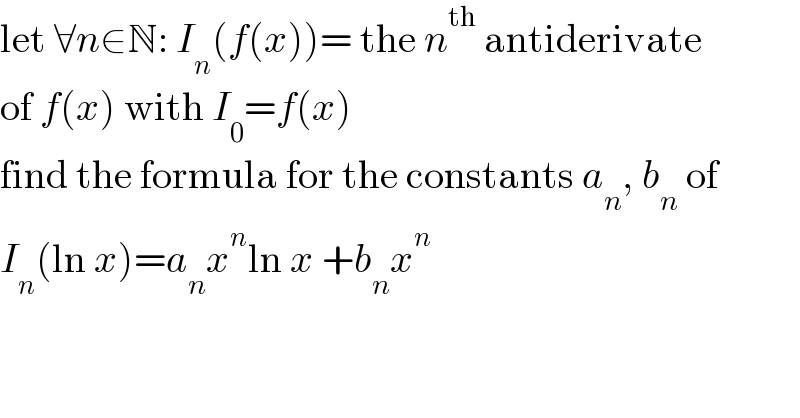 | ||
Answered by aleks041103 last updated on 07/Jul/22 | ||
![I_(n+1) (ln x)=∫I_n (ln x)dx= =∫(a_n x^n ln x + b_n x^n )dx= =a_n ∫x^n ln x dx + b_n ∫x^n dx ∫x^n ln x dx=∫ln x d((x^(n+1) /(n+1)))= =(x^(n+1) /(n+1))ln x−(1/(n+1))∫x^(n+1) (dx/x)= =(1/(n+1))x^(n+1) ln x −(1/((n+1)^2 ))x^(n+1) ⇒I_(n+1) (ln x)=a_n [(1/(n+1))x^(n+1) ln x −(1/((n+1)^2 ))x^(n+1) ]+(b_n /(n+1))x^(n+1) = =((a_n /(n+1)))x^(n+1) ln x + ((b_n /(n+1))−(a_n /((n+1)^2 )))x^(n+1) = =a_(n+1) x^(n+1) ln x + b_(n+1) x^(n+1) ⇒ { ((a_(n+1) =(a_n /(n+1)))),((b_(n+1) =(b_n /(n+1))−(a_n /((n+1)^2 )))) :} (1/a_(n+1) )=(n+1)(1/a_n )⇒(1/a_n )=const.n!⇒a_n =((const)/(n!)) I_0 (ln x)=ln x⇒a_0 =1⇒a_n =(1/(n!)) ⇒b_(n+1) =(b_n /(n+1))−(1/((n+1)!(n+1))) (n+1)b_(n+1) −b_n =−(1/((n+1)!)) b_n =(c_n /(n!)) ⇒(n+1)(c_(n+1) /((n+1)!))−(c_n /(n!))=−(1/((n+1)!))=−(1/((n+1) n!)) ⇒c_(n+1) −c_n =−(1/(n+1)) ⇒c_n =const.−Σ_(i≥1) ^n (1/i) c_0 =const.=0⇒c_n =−Σ_(i≥1) ^n (1/i)=−H_n ⇒b_n =−(H_n /(n!)) ⇒ { ((a_n =(1/(n!)))),((b_n =−(H_n /(n!)) , H_(n≥1) =Σ_(k=1) ^n (1/k), H_0 =0)) :}](Q173158.png) | ||
| ||
Commented by Frix last updated on 08/Jul/22 | ||
 | ||
Commented by Tawa11 last updated on 11/Jul/22 | ||
 | ||