
Question and Answers Forum
Question Number 173152 by AgniMath last updated on 07/Jul/22
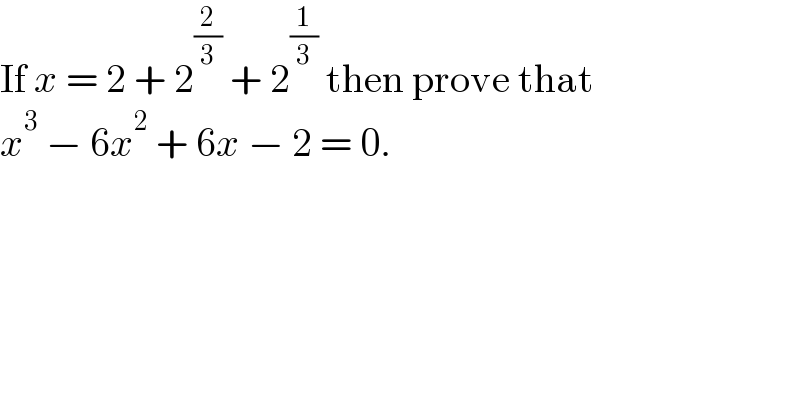
Answered by Frix last updated on 07/Jul/22
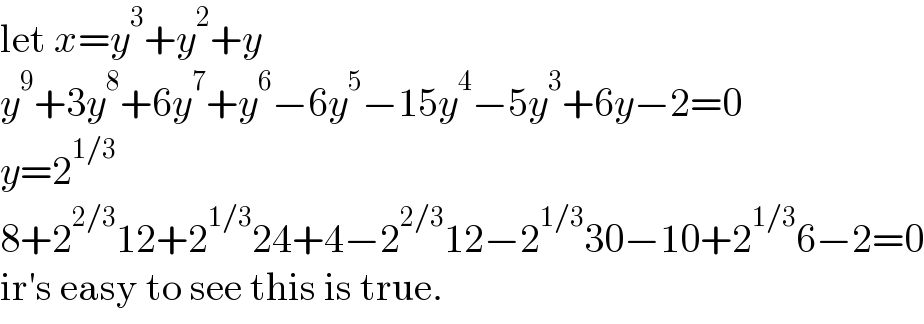
Answered by som(math1967) last updated on 07/Jul/22
![x−2=2^(2/3) +2^(1/3) (x−2)^3 =(2^(2/3) +2^(1/3) )^3 ⇒x^3 −6x^2 +12x−8=(2^(2/3) )^3 +(2^(1/3) )^3 +3.2^(2/3) .2^(1/3) (2^(2/3) +2^(1/3) ) ⇒x^3 −6x^2 +12x−8=4+2+3.2(x−2) [∵ (x−2)=2^(2/3) +2^(1/3) ] ⇒x^3 −6x^2 +12x−8=6+6x−12 ⇒x^3 −6x^2 +12x−6x−8+6=0 ∴x^3 −6x^2 +6x−2=0](Q173159.png)
Commented by Tawa11 last updated on 11/Jul/22

| ||
Question and Answers Forum | ||
Question Number 173152 by AgniMath last updated on 07/Jul/22 | ||
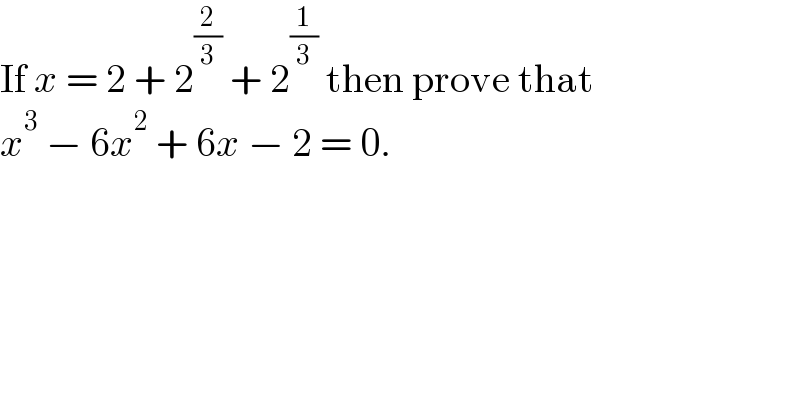 | ||
Answered by Frix last updated on 07/Jul/22 | ||
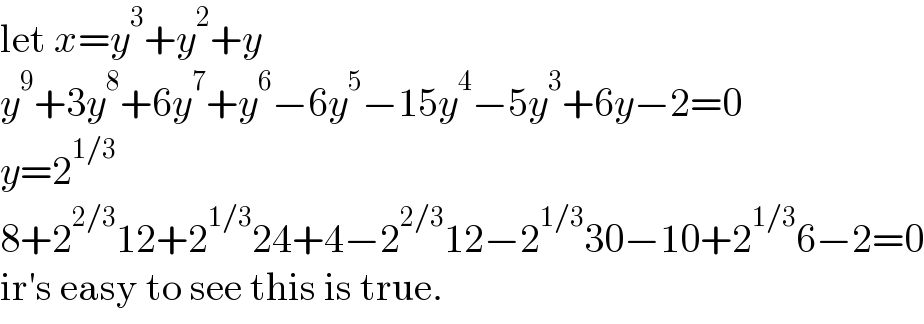 | ||
| ||
Answered by som(math1967) last updated on 07/Jul/22 | ||
![x−2=2^(2/3) +2^(1/3) (x−2)^3 =(2^(2/3) +2^(1/3) )^3 ⇒x^3 −6x^2 +12x−8=(2^(2/3) )^3 +(2^(1/3) )^3 +3.2^(2/3) .2^(1/3) (2^(2/3) +2^(1/3) ) ⇒x^3 −6x^2 +12x−8=4+2+3.2(x−2) [∵ (x−2)=2^(2/3) +2^(1/3) ] ⇒x^3 −6x^2 +12x−8=6+6x−12 ⇒x^3 −6x^2 +12x−6x−8+6=0 ∴x^3 −6x^2 +6x−2=0](Q173159.png) | ||
| ||
Commented by Tawa11 last updated on 11/Jul/22 | ||
 | ||