Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 173302 by AgniMath last updated on 09/Jul/22

Commented by mr W last updated on 10/Jul/22

nice solution!

$${nice}\:{solution}! \\ $$

Commented by dragan91 last updated on 10/Jul/22

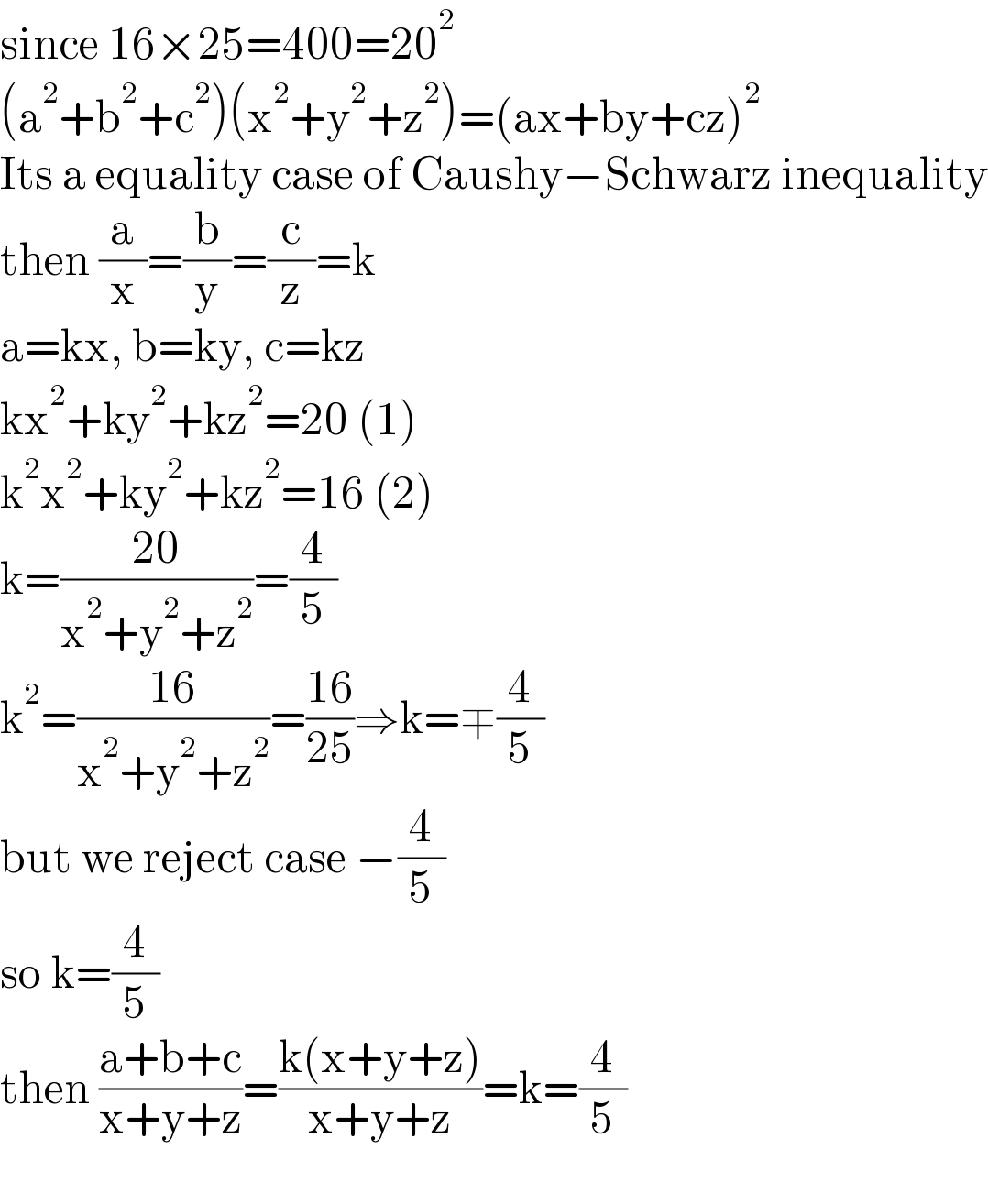
since 16×25=400=20^2 (a^2 +b^2 +c^2 )(x^2 +y^2 +z^2 )=(ax+by+cz)^2 Its a equality case of Caushy−Schwarz inequality then (a/x)=(b/y)=(c/z)=k a=kx, b=ky, c=kz kx^2 +ky^2 +kz^2 =20 (1) k^2 x^2 +ky^2 +kz^2 =16 (2) k=((20)/(x^2 +y^2 +z^2 ))=(4/5) k^2 =((16)/(x^2 +y^2 +z^2 ))=((16)/(25))⇒k=∓(4/5) but we reject case −(4/5) so k=(4/5) then ((a+b+c)/(x+y+z))=((k(x+y+z))/(x+y+z))=k=(4/5)

$$\mathrm{since}\:\mathrm{16}×\mathrm{25}=\mathrm{400}=\mathrm{20}^{\mathrm{2}} \\ $$$$\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \right)=\left(\mathrm{ax}+\mathrm{by}+\mathrm{cz}\right)^{\mathrm{2}} \\ $$$$\mathrm{Its}\:\mathrm{a}\:\mathrm{equality}\:\mathrm{case}\:\mathrm{of}\:\mathrm{Caushy}−\mathrm{Schwarz}\:\mathrm{inequality} \\ $$$$\mathrm{then}\:\frac{\mathrm{a}}{\mathrm{x}}=\frac{\mathrm{b}}{\mathrm{y}}=\frac{\mathrm{c}}{\mathrm{z}}=\mathrm{k} \\ $$$$\mathrm{a}=\mathrm{kx},\:\mathrm{b}=\mathrm{ky},\:\mathrm{c}=\mathrm{kz} \\ $$$$\mathrm{kx}^{\mathrm{2}} +\mathrm{ky}^{\mathrm{2}} +\mathrm{kz}^{\mathrm{2}} =\mathrm{20}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\mathrm{ky}^{\mathrm{2}} +\mathrm{kz}^{\mathrm{2}} =\mathrm{16}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{k}=\frac{\mathrm{20}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{k}^{\mathrm{2}} =\frac{\mathrm{16}}{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} }=\frac{\mathrm{16}}{\mathrm{25}}\Rightarrow\mathrm{k}=\mp\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{reject}\:\mathrm{case}\:−\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{so}\:\mathrm{k}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{then}\:\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{x}+\mathrm{y}+\mathrm{z}}=\frac{\mathrm{k}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)}{\mathrm{x}+\mathrm{y}+\mathrm{z}}=\mathrm{k}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$ \\ $$

Answered by mr W last updated on 10/Jul/22

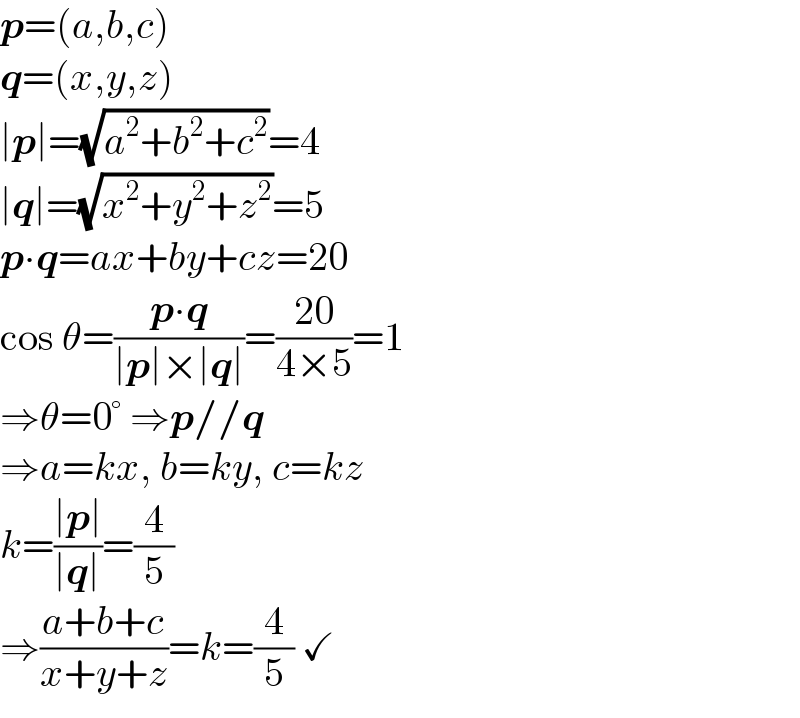
p=(a,b,c) q=(x,y,z) ∣p∣=(√(a^2 +b^2 +c^2 ))=4 ∣q∣=(√(x^2 +y^2 +z^2 ))=5 p∙q=ax+by+cz=20 cos θ=((p∙q)/(∣p∣×∣q∣))=((20)/(4×5))=1 ⇒θ=0° ⇒p//q ⇒a=kx, b=ky, c=kz k=((∣p∣)/(∣q∣))=(4/5) ⇒((a+b+c)/(x+y+z))=k=(4/5) ✓

$$\boldsymbol{{p}}=\left({a},{b},{c}\right) \\ $$$$\boldsymbol{{q}}=\left({x},{y},{z}\right) \\ $$$$\mid\boldsymbol{{p}}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }=\mathrm{4} \\ $$$$\mid\boldsymbol{{q}}\mid=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }=\mathrm{5} \\ $$$$\boldsymbol{{p}}\centerdot\boldsymbol{{q}}={ax}+{by}+{cz}=\mathrm{20}\: \\ $$$$\mathrm{cos}\:\theta=\frac{\boldsymbol{{p}}\centerdot\boldsymbol{{q}}}{\mid\boldsymbol{{p}}\mid×\mid\boldsymbol{{q}}\mid}=\frac{\mathrm{20}}{\mathrm{4}×\mathrm{5}}=\mathrm{1}\: \\ $$$$\Rightarrow\theta=\mathrm{0}°\:\Rightarrow\boldsymbol{{p}}//\boldsymbol{{q}} \\ $$$$\Rightarrow{a}={kx},\:{b}={ky},\:{c}={kz} \\ $$$${k}=\frac{\mid\boldsymbol{{p}}\mid}{\mid\boldsymbol{{q}}\mid}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow\frac{{a}+{b}+{c}}{{x}+{y}+{z}}={k}=\frac{\mathrm{4}}{\mathrm{5}}\:\checkmark \\ $$

Answered by AgniMath last updated on 09/Jul/22

Another way Let b = c = 0 and y = z = 0 a^2 + b^2 + c^2 = 16 or a^2 = 16 ∴ a = 4 or −4 x^2 + y^2 + z^2 = 25 or x^2 = 25 ∴ x = 5 or −5 ax + by + cz = 20 ∴ ax = 20 [ b = c = y = z = 0] so ax can be 4 × 5 or −4 × −5 ((a + b + c)/(x + y + z)) = (4/5) or ((−4)/(−5)) = (4/5) (Ans)

$$\mathrm{Another}\:\mathrm{way} \\ $$$$ \\ $$$$\mathrm{Let}\:\mathrm{b}\:=\:\mathrm{c}\:=\:\mathrm{0}\:\mathrm{and}\:\mathrm{y}\:=\:\mathrm{z}\:=\:\mathrm{0} \\ $$$${a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:+\:{c}^{\mathrm{2}} \:=\:\mathrm{16} \\ $$$${or}\:{a}^{\mathrm{2}} \:=\:\mathrm{16}\: \\ $$$$\therefore\:{a}\:=\:\mathrm{4}\:{or}\:−\mathrm{4} \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \:=\:\mathrm{25} \\ $$$${or}\:{x}^{\mathrm{2}} \:=\:\mathrm{25} \\ $$$$\therefore\:{x}\:=\:\mathrm{5}\:{or}\:−\mathrm{5} \\ $$$${ax}\:+\:{by}\:+\:{cz}\:=\:\mathrm{20} \\ $$$$\therefore\:{ax}\:=\:\mathrm{20}\:\left[\:{b}\:=\:{c}\:=\:{y}\:=\:{z}\:=\:\mathrm{0}\right] \\ $$$${so}\:{ax}\:{can}\:{be}\:\mathrm{4}\:×\:\mathrm{5}\:{or}\:−\mathrm{4}\:×\:−\mathrm{5} \\ $$$$ \\ $$$$\frac{{a}\:+\:{b}\:+\:{c}}{{x}\:+\:{y}\:+\:{z}}\:=\:\frac{\mathrm{4}}{\mathrm{5}}\:{or}\:\frac{\cancel{−}\mathrm{4}}{\cancel{−}\mathrm{5}}\:=\:\frac{\mathrm{4}}{\mathrm{5}}\:\left(\mathrm{Ans}\right) \\ $$

Commented by mr W last updated on 09/Jul/22

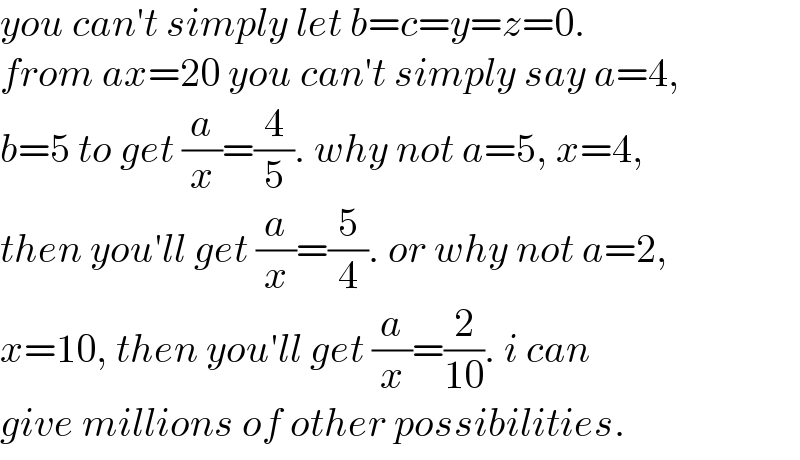
you can′t simply let b=c=y=z=0. from ax=20 you can′t simply say a=4, b=5 to get (a/x)=(4/5). why not a=5, x=4, then you′ll get (a/x)=(5/4). or why not a=2, x=10, then you′ll get (a/x)=(2/(10)). i can give millions of other possibilities.

$${you}\:{can}'{t}\:{simply}\:{let}\:{b}={c}={y}={z}=\mathrm{0}. \\ $$$${from}\:{ax}=\mathrm{20}\:{you}\:{can}'{t}\:{simply}\:{say}\:{a}=\mathrm{4}, \\ $$$${b}=\mathrm{5}\:{to}\:{get}\:\frac{{a}}{{x}}=\frac{\mathrm{4}}{\mathrm{5}}.\:{why}\:{not}\:{a}=\mathrm{5},\:{x}=\mathrm{4}, \\ $$$${then}\:{you}'{ll}\:{get}\:\frac{{a}}{{x}}=\frac{\mathrm{5}}{\mathrm{4}}.\:{or}\:{why}\:{not}\:{a}=\mathrm{2}, \\ $$$${x}=\mathrm{10},\:{then}\:{you}'{ll}\:{get}\:\frac{{a}}{{x}}=\frac{\mathrm{2}}{\mathrm{10}}.\:{i}\:{can} \\ $$$${give}\:{millions}\:{of}\:{other}\:{possibilities}. \\ $$

Commented by AgniMath last updated on 10/Jul/22

thanks

$$\mathrm{thanks} \\ $$

Commented by mr W last updated on 10/Jul/22

you′r welcome!

$${you}'{r}\:{welcome}! \\ $$

Commented by Tawa11 last updated on 11/Jul/22

Great sirs

$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com