Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 173403 by mathlove last updated on 11/Jul/22

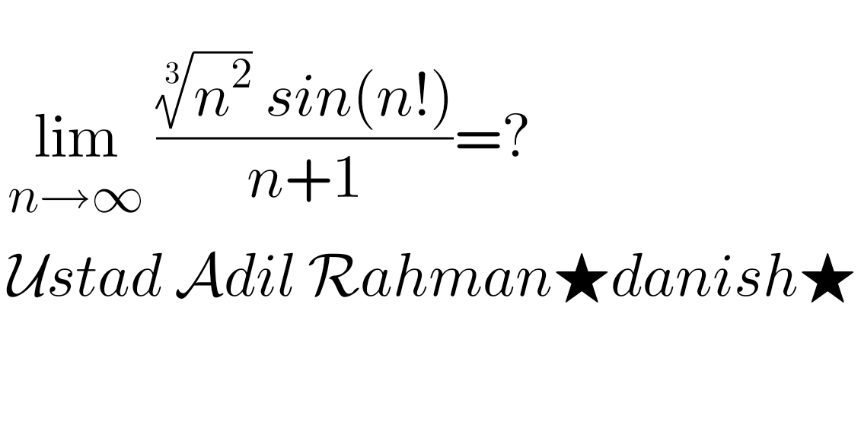
Commented by mr W last updated on 11/Jul/22

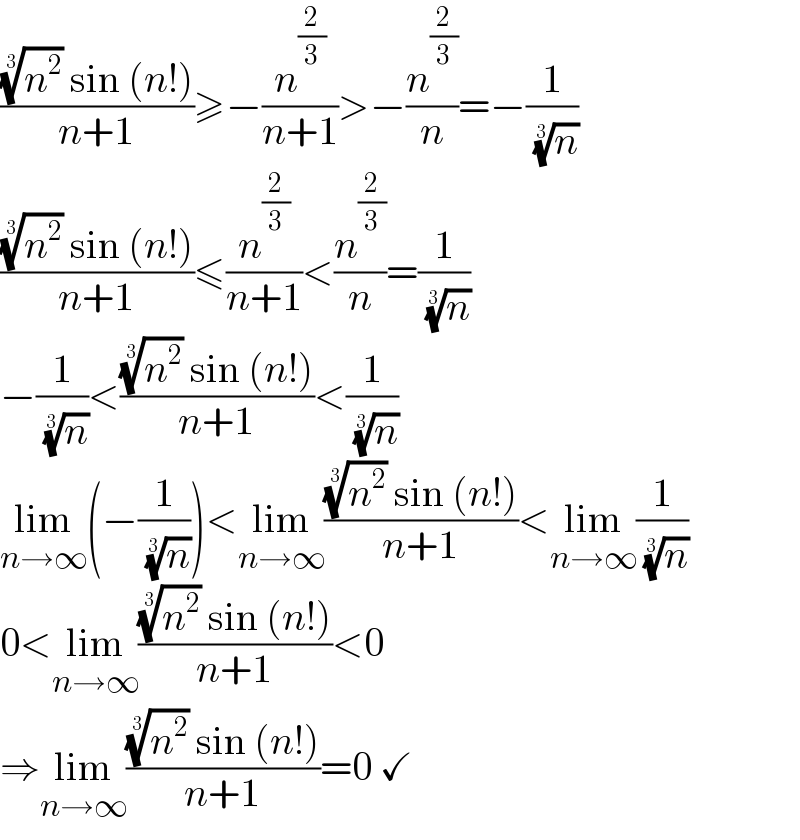
(((n^2 )^(1/3) sin (n!))/(n+1))≥−(n^(2/3) /(n+1))>−(n^(2/3) /n)=−(1/( (n)^(1/3) )) (((n^2 )^(1/3) sin (n!))/(n+1))≤(n^(2/3) /(n+1))<(n^(2/3) /n)=(1/( (n)^(1/3) )) −(1/( (n)^(1/3) ))<(((n^2 )^(1/3) sin (n!))/(n+1))<(1/( (n)^(1/3) )) lim_(n→∞) (−(1/( (n)^(1/3) )))<lim_(n→∞) (((n^2 )^(1/3) sin (n!))/(n+1))<lim_(n→∞) (1/( (n)^(1/3) )) 0<lim_(n→∞) (((n^2 )^(1/3) sin (n!))/(n+1))<0 ⇒lim_(n→∞) (((n^2 )^(1/3) sin (n!))/(n+1))=0 ✓

$$\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }\:\mathrm{sin}\:\left({n}!\right)}{{n}+\mathrm{1}}\geqslant−\frac{{n}^{\frac{\mathrm{2}}{\mathrm{3}}} }{{n}+\mathrm{1}}>−\frac{{n}^{\frac{\mathrm{2}}{\mathrm{3}}} }{{n}}=−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{n}}} \\ $$$$\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }\:\mathrm{sin}\:\left({n}!\right)}{{n}+\mathrm{1}}\leqslant\frac{{n}^{\frac{\mathrm{2}}{\mathrm{3}}} }{{n}+\mathrm{1}}<\frac{{n}^{\frac{\mathrm{2}}{\mathrm{3}}} }{{n}}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{n}}} \\ $$$$−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{n}}}<\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }\:\mathrm{sin}\:\left({n}!\right)}{{n}+\mathrm{1}}<\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{n}}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{n}}}\right)<\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }\:\mathrm{sin}\:\left({n}!\right)}{{n}+\mathrm{1}}<\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{{n}}} \\ $$$$\mathrm{0}<\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }\:\mathrm{sin}\:\left({n}!\right)}{{n}+\mathrm{1}}<\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }\:\mathrm{sin}\:\left({n}!\right)}{{n}+\mathrm{1}}=\mathrm{0}\:\checkmark \\ $$

Commented by mathlove last updated on 11/Jul/22

Thank you so much for a long life. I don't have words to thank you for always helping me

$$ \\ $$Thank you so much for a long life. I don't have words to thank you for always helping me

Commented by kaivan.ahmadi last updated on 11/Jul/22

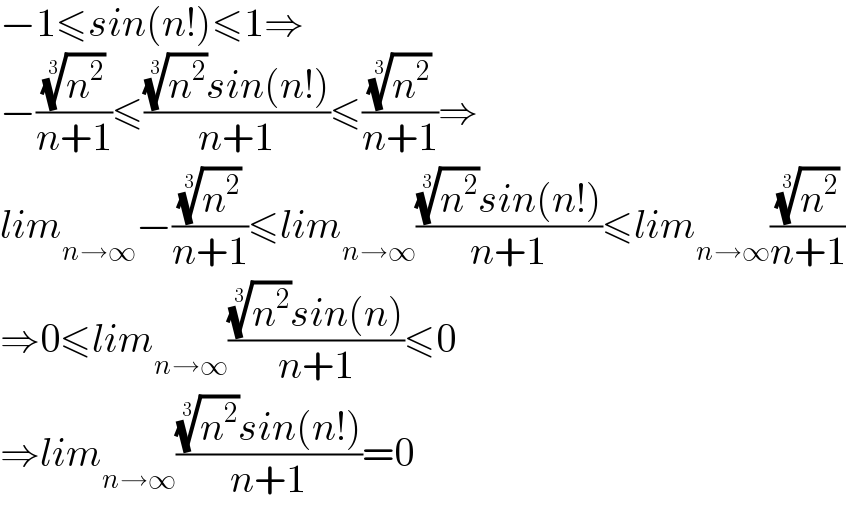
−1≤sin(n!)≤1⇒ −((n^2 )^(1/3) /(n+1))≤(((n^2 )^(1/3) sin(n!))/(n+1))≤((n^2 )^(1/3) /(n+1))⇒ lim_(n→∞) −((n^2 )^(1/3) /(n+1))≤lim_(n→∞) (((n^2 )^(1/3) sin(n!))/(n+1))≤lim_(n→∞) ((n^2 )^(1/3) /(n+1)) ⇒0≤lim_(n→∞) (((n^2 )^(1/3) sin(n))/(n+1))≤0 ⇒lim_(n→∞) (((n^2 )^(1/3) sin(n!))/(n+1))=0

$$−\mathrm{1}\leqslant{sin}\left({n}!\right)\leqslant\mathrm{1}\Rightarrow \\ $$$$−\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }}{{n}+\mathrm{1}}\leqslant\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }{sin}\left({n}!\right)}{{n}+\mathrm{1}}\leqslant\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }}{{n}+\mathrm{1}}\Rightarrow \\ $$$${lim}_{{n}\rightarrow\infty} −\frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }}{{n}+\mathrm{1}}\leqslant{lim}_{{n}\rightarrow\infty} \frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }{sin}\left({n}!\right)}{{n}+\mathrm{1}}\leqslant{lim}_{{n}\rightarrow\infty} \frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }}{{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{0}\leqslant{lim}_{{n}\rightarrow\infty} \frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }{sin}\left({n}\right)}{{n}+\mathrm{1}}\leqslant\mathrm{0} \\ $$$$\Rightarrow{lim}_{{n}\rightarrow\infty} \frac{\sqrt[{\mathrm{3}}]{{n}^{\mathrm{2}} }{sin}\left({n}!\right)}{{n}+\mathrm{1}}=\mathrm{0} \\ $$

Commented by mathlove last updated on 13/Jul/22

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com