Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 17348 by Tinkutara last updated on 04/Jul/17

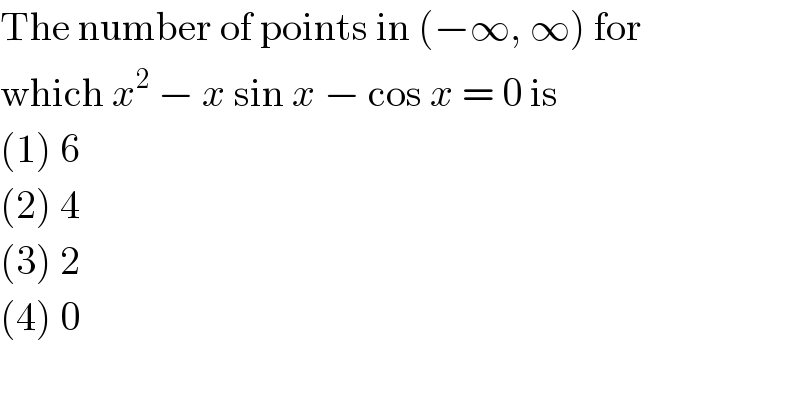
The number of points in (−∞, ∞) for which x^2 − x sin x − cos x = 0 is (1) 6 (2) 4 (3) 2 (4) 0

$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{points}\:\mathrm{in}\:\left(−\infty,\:\infty\right)\:\mathrm{for} \\ $$$$\mathrm{which}\:{x}^{\mathrm{2}} \:−\:{x}\:\mathrm{sin}\:{x}\:−\:\mathrm{cos}\:{x}\:=\:\mathrm{0}\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{6} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{4} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{2} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{0} \\ $$

Answered by ajfour last updated on 04/Jul/17

(3) 2 let f(x)=x^2 −xsin x−cos x f(0)=−1 f ′(x)=2x−xcos x = x(2−cos x) as x→ −∞ , f(x)→∞ only decreasing for x<0 stops decreasing when x=0 and by this time f(x)=−1 ⇒ crossed x-axis once x=0 is the minimum f(x) starts increasing from f(0)=−1 and keeps increasing hereafter so crosses x-axis just once more.

$$\left(\mathrm{3}\right)\:\mathrm{2} \\ $$$$\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} −\mathrm{xsin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x} \\ $$$$\:\:\:\:\:\mathrm{f}\left(\mathrm{0}\right)=−\mathrm{1} \\ $$$$\:\:\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{xcos}\:\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\:\:\mathrm{as}\:\mathrm{x}\rightarrow\:−\infty\:,\:\mathrm{f}\left(\mathrm{x}\right)\rightarrow\infty \\ $$$$\:\:\mathrm{only}\:\mathrm{decreasing}\:\mathrm{for}\:\mathrm{x}<\mathrm{0} \\ $$$$\:\mathrm{stops}\:\mathrm{decreasing}\:\mathrm{when}\:\mathrm{x}=\mathrm{0} \\ $$$$\:\mathrm{and}\:\mathrm{by}\:\mathrm{this}\:\mathrm{time}\:\mathrm{f}\left(\mathrm{x}\right)=−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{crossed}\:\mathrm{x}-\mathrm{axis}\:\mathrm{once} \\ $$$$\:\:\:\:\:\:\:\mathrm{x}=\mathrm{0}\:\mathrm{is}\:\mathrm{the}\:\mathrm{minimum} \\ $$$$\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{starts}\:\mathrm{increasing}\:\mathrm{from}\: \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=−\mathrm{1}\:\mathrm{and}\:\mathrm{keeps}\:\mathrm{increasing} \\ $$$$\:\mathrm{hereafter}\:\mathrm{so}\:\mathrm{crosses}\:\mathrm{x}-\mathrm{axis}\:\mathrm{just} \\ $$$$\mathrm{once}\:\mathrm{more}. \\ $$

Commented by Tinkutara last updated on 05/Jul/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Answered by mrW1 last updated on 04/Jul/17

y=f(x)=x^2 − x sin x − cos x f(−x)=(−x)^2 −(−x)sin (−x)−cos (−x) =x^2 −x sin x−cos x f(x) is symmetric. f(0)=−1 lim_(x→+∞) f(x)=+∞ ⇒there is at least one point for x>0 and f(x)=0 f′(x)=2x−sin x−xcos x+sin x=x(2−cos x) for x>0 ⇒f′(x)>0 ⇒f(x) is increasing for x>0 ⇒there is only one point for x∈(0,+∞) with f(x)=0 due to symmetry there are 2 point2 for x∈(−∞,+∞) with f(x)=0 ⇒answer (3) is right.

$$\mathrm{y}=\mathrm{f}\left(\mathrm{x}\right)={x}^{\mathrm{2}} \:−\:{x}\:\mathrm{sin}\:{x}\:−\:\mathrm{cos}\:{x} \\ $$$$\mathrm{f}\left(−\mathrm{x}\right)=\left(−\mathrm{x}\right)^{\mathrm{2}} −\left(−\mathrm{x}\right)\mathrm{sin}\:\left(−\mathrm{x}\right)−\mathrm{cos}\:\left(−\mathrm{x}\right) \\ $$$$=\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{symmetric}. \\ $$$$\mathrm{f}\left(\mathrm{0}\right)=−\mathrm{1} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\mathrm{f}\left(\mathrm{x}\right)=+\infty \\ $$$$\Rightarrow\mathrm{there}\:\mathrm{is}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{point}\:\mathrm{for}\:\mathrm{x}>\mathrm{0}\: \\ $$$$\mathrm{and}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{2x}−\mathrm{sin}\:\mathrm{x}−\mathrm{xcos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}=\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\mathrm{for}\:\mathrm{x}>\mathrm{0}\:\Rightarrow\mathrm{f}'\left(\mathrm{x}\right)>\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{increasing}\:\mathrm{for}\:\mathrm{x}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{there}\:\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{point}\:\mathrm{for}\:\mathrm{x}\in\left(\mathrm{0},+\infty\right)\:\mathrm{with} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}\: \\ $$$$\mathrm{there}\:\mathrm{are}\:\mathrm{2}\:\mathrm{point2}\:\mathrm{for}\:\mathrm{x}\in\left(−\infty,+\infty\right)\:\mathrm{with} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow\mathrm{answer}\:\left(\mathrm{3}\right)\:\mathrm{is}\:\mathrm{right}. \\ $$

Commented by Tinkutara last updated on 05/Jul/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Answered by b.e.h.i.8.3.4.17@gmail.com last updated on 06/Jul/17

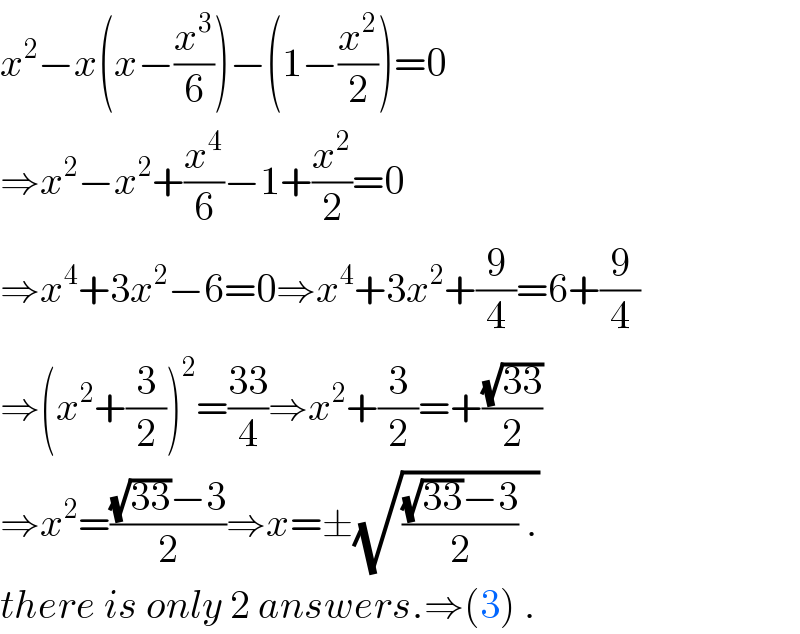
x^2 −x(x−(x^3 /6))−(1−(x^2 /2))=0 ⇒x^2 −x^2 +(x^4 /6)−1+(x^2 /2)=0 ⇒x^4 +3x^2 −6=0⇒x^4 +3x^2 +(9/4)=6+(9/4) ⇒(x^2 +(3/2))^2 =((33)/4)⇒x^2 +(3/2)=+((√(33))/2) ⇒x^2 =(((√(33))−3)/2)⇒x=±(√((((√(33))−3)/2) .)) there is only 2 answers.⇒(3) .

$${x}^{\mathrm{2}} −{x}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{4}} }{\mathrm{6}}−\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}=\mathrm{0}\Rightarrow{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{6}+\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{33}}{\mathrm{4}}\Rightarrow{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}=+\frac{\sqrt{\mathrm{33}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\frac{\sqrt{\mathrm{33}}−\mathrm{3}}{\mathrm{2}}\Rightarrow{x}=\pm\sqrt{\frac{\sqrt{\mathrm{33}}−\mathrm{3}}{\mathrm{2}}\:.} \\ $$$${there}\:{is}\:{only}\:\mathrm{2}\:{answers}.\Rightarrow\left(\mathrm{3}\right)\:. \\ $$

Commented by Tinkutara last updated on 07/Jul/17

Can you explain the first line?

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{the}\:\mathrm{first}\:\mathrm{line}? \\ $$

Commented by alex041103 last updated on 07/Jul/17

This is wrong. He tried to use the Taylor series expansion for sin x and cos x. They have infinatly many terms, but he uses only two of them. This is an aproximation! Here are the expansions for sine and cosine: sin x =Σ_(n=0) ^∞ (−1)^n (x^(2n+1) /((2n+1)!)) cos x = Σ_(n=0) ^∞ (−1)^n (x^(2n) /((2n)!))

$$\mathrm{This}\:\mathrm{is}\:\mathrm{wrong}. \\ $$$$\mathrm{He}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{use}\:\mathrm{the}\:\mathrm{Taylor}\:\mathrm{series} \\ $$$$\mathrm{expansion}\:\mathrm{for}\:\mathrm{sin}\:\mathrm{x}\:\mathrm{and}\:\mathrm{cos}\:\mathrm{x}.\: \\ $$$$\mathrm{They}\:\mathrm{have}\:\mathrm{infinatly}\:\mathrm{many}\:\mathrm{terms},\:\mathrm{but} \\ $$$$\mathrm{he}\:\mathrm{uses}\:\mathrm{only}\:\mathrm{two}\:\mathrm{of}\:\mathrm{them}. \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{an}\:\mathrm{aproximation}! \\ $$$$\mathrm{Here}\:\mathrm{are}\:\mathrm{the}\:\mathrm{expansions}\:\mathrm{for}\:\mathrm{sine}\:\mathrm{and}\:\mathrm{cosine}: \\ $$$${sin}\:{x}\:=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$${cos}\:{x}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com