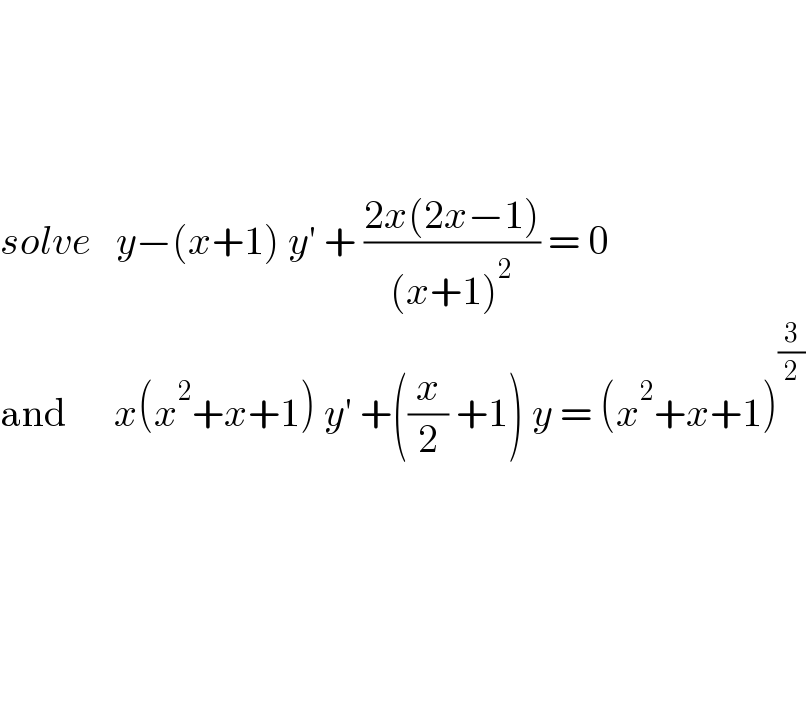
solve y−(x+1) y′ + ((2x(2x−1))/((x+1)^2 )) = 0 and x(x^2 +x+1) y′ +((x/2) +1) y = (x^2 +x+1)^(3/2)


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 173507 by JordanRoddy last updated on 12/Jul/22

$s o l v e y - (x + 1) y^{'} + \frac{2 x (2 x - 1)}{{(x + 1)}^{2}} = 0$ $and x (x^{2} + x + 1) y^{'} + (\frac{x}{2} + 1) y = {(x^{2} + x + 1)}^{\frac{3}{2}}$
Commented by JordanRoddy last updated on 12/Jul/22

$s o l v e y - (x + 1) y^{'} + \frac{2 x (2 x - 1)}{{(x + 1)}^{2}} = 0$ $and x (x^{2} + x + 1) y^{'} + (\frac{x}{2} + 1) y = {(x^{2} + x + 1)}^{\frac{3}{2}}$
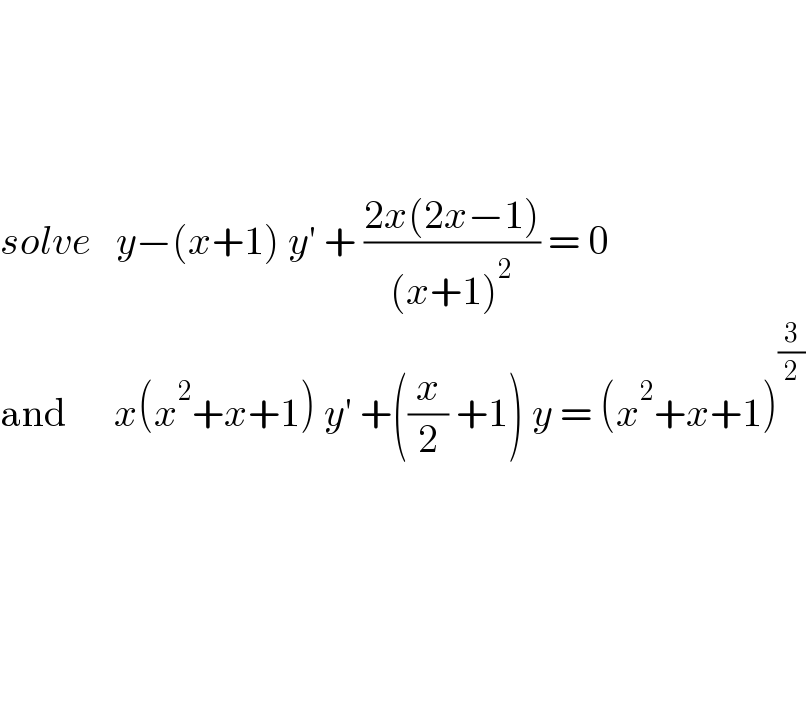Commented by mokys last updated on 12/Jul/22

$1) \frac{d y}{d x} - \frac{1}{x + 1} y = \frac{2 x (2 x - 1)}{{(x + 1)}^{3}}$ $P (x) = - \frac{1}{x + 1}, Q (x) = \frac{2 x (2 x - 1)}{{(x + 1)}^{3}}$ $I . f = e^{\int P (x) d x} = e^{\int - \frac{1}{x + 1} d x} = e^{l n \frac{1}{x + 1}} = \frac{1}{x + 1}$ $(I . f) y = \int (I . f) Q (x) d x$ $\frac{y}{x + 1} = 2 \int \frac{x (2 x - 1)}{{(x + 1)}^{4}} d x$ $l e t : m = x + 1 \to x = m - 1 \to d x = d m$ $\frac{y}{x + 1} = 2 \int \frac{(m - 1) (2 m - 3)}{m^{4}} d m$ $\frac{y}{x + 1} = 2 \int \frac{2 m^{2} - 5 m + 3}{m^{4}} d m$ $\frac{y}{x + 1} = 2 \int (\frac{2}{m^{2}} - \frac{5}{m^{3}} + \frac{3}{m^{4}}) d m$ $\frac{y}{x + 1} = - \frac{4}{m} + \frac{5}{m^{2}} - \frac{2}{m^{3}} + K$ $N o w : m = x + 1$ $∴ y = \frac{5}{x + 1} - \frac{2}{{(x + 1)}^{2}} - 4 + K (x + 1)$ $★ M o h a m m a d A l d o l a i m y ★$
Commented by Tawa11 last updated on 13/Jul/22

$Great sir .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum